03-0002 Python实现A*算法

1.算法描述

A*搜寻算法俗称A星算法,是比较流行的启发式搜索算法之一，被广泛应用于路径优化领域。它的独特之处是检查最短路径中每个可能的节点时引入了全局信息，对当前节点距终点的距离做出估计，并作为评价该节点处于最短路线上的可能性的量度。

A*改变它自己行为的能力基于启发式代价函数，启发式函数在游戏中非常有用。在速度和精确度之间取得折衷将会让你的游戏运行得更快。在很多游戏中，你并不真正需要得到最好的路径，仅需要近似的就足够了。而你需要什么则取决于游戏中发生着什么，或者运行游戏的机器有多快。

在本实验中，为了解决罗马尼亚度假问题而引入的A算法，目的是为了寻找一个城市到另一个城市的最短路径，A算法

扩展：本来想些启发式算法的，但是突然迷茫了一下，可以以后再写，好好的学一学。当我写这些东西的时候，我发现，自己还不是很懂。
以上多数文字直接来源于度娘百科，没有过多的修改。我对于A*算法的描述，着实少之又少，感觉自己又回到了最初的懵懂状态。
我需要一个比较好的数据集来解释自己想要时候的，直接用数据来描述自己想要表达的。

2.问题描述

旅行商问题：
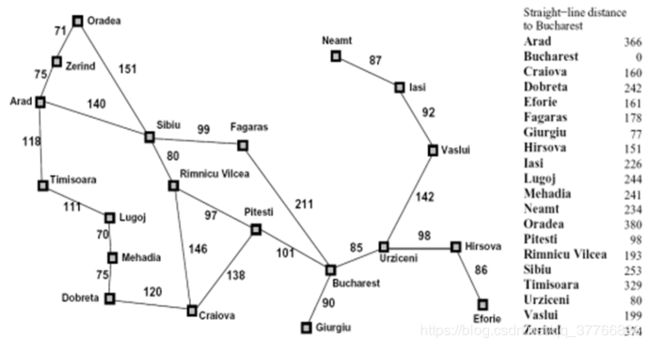
In the following map with 20 cities, please find a route from Zerind to Bucharest using A search.*
[在一个拥有20个城市的图中，使用A星算法，找到一条最优路径从塞尔维亚到罗马尼亚]

解释：

上述图中，线上的数字表示两个城市的实际距离。
右侧的数字表示到Bucharest[终点]的估计距离。
每个城市的首字母都不一样，可以数字化。

3.算法原理

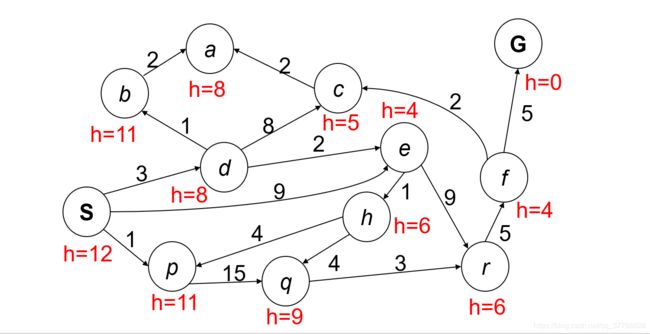
A*算法是一种搜索算法，在算法过程中引入了F，G，H三个量。
$$F=G+H$$

$F：用作判断条件的量。在算法使用的数据结构[优先级队列]中，F小的将会先弹出。$
$G：从出发点到当前节点的实际距离。$
$H：从当前节点到目标节点的估计距离。$

下面引入具体数据，来演示A*算法：
.
说明：

$p_S^{12}：P节点的F值是12，父节点是S$
$PQ：优先级队列$
$SK：栈$

注意事项：

$1.每次进入PQ的结点是上一次从PQ弹出结点的临近结点。$
$2.从PQ中弹出的结点放入SK中$
$3.进入PQ的结点若已经存在，比较F值，小的留下$
$4.已经存在于SK中的结点不进入PQ中$
$5.到达目标结点就终止运算$

过程：

$PQ：S_{none}^{12}$
$SK：none$
.
$PQ：S_{none}^{12}，d_s^{12}，e_s^{13}，p_s^{12}$
$SK：S$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，p_s^{12}，b_d^{15}，c_d^{16}，e_d^9$ $[这里需要替换e结点]$
$SK：S，d$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，p_s^{12}，b_d^{15}，c_d^{16}，$$e_d^9，$ $h_e^{12}，$ $r_e^{20}$ $[此时弹出p，h皆可]$
$SK：S，d，e$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，$ $p_s^{12}$，$b_d^{15}，c_d^{16}，$$e_d^9，$ $h_e^{12}，$ $r_e^{20}$ ，$q_p^{25}$
$SK：S，d，e，p$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，$ $p_s^{12}$，$b_d^{15}，c_d^{16}，$$e_d^9，$ $h_e^{12}，$ $r_e^{20}$ ，$q_p^{25}$，$q_h^{19}$ $[此时p在SK，q在PQ，p不进，q换掉]$
$SK：S，d，e，p，h$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，$ $p_s^{12}$，$b_d^{15}，c_d^{16}，$$e_d^9，$ $h_e^{12}，$ $r_e^{20}$ ，$q_p^{25}$，$q_h^{19}$，$a_b^{14}$
$SK：S，d，e，p，h，b$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，$ $p_s^{12}$，$b_d^{15}，c_d^{16}，$$e_d^9，$ $h_e^{12}，$ $r_e^{20}$ ，$q_p^{25}$，$q_h^{19}$，$a_b^{14}$ $[a没有临近结点，弹出下一个]$
$SK：S，d，e，p，h，b，a$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，$ $p_s^{12}$，$b_d^{15}，c_d^{16}，$$e_d^9，$ $h_e^{12}，$ $r_e^{20}$ ，$q_p^{25}$，$q_h^{19}$，$a_b^{14}$，$r_q^{19}$
$SK：S，d，e，p，h，b，a，q$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，$ $p_s^{12}$，$b_d^{15}，c_d^{16}，$$e_d^9，$ $h_e^{12}，$ $r_e^{20}$ ，$q_p^{25}$，$q_h^{19}$，$a_b^{14}$，$r_q^{19}$，$f_r^{18}$
$SK：S，d，e，p，h，b，a，q，r$
.
$PQ：S_{none}^{12}，$ $d_s^{11}，$ $e_s^{13}，$ $p_s^{12}$，$b_d^{15}，c_d^{16}，$$e_d^9，$ $h_e^{12}，$ $r_e^{20}$ ，$q_p^{25}$，$q_h^{19}$，$a_b^{14}$，$r_q^{19}$，$f_r^{24}$，$c_f^{25}$，$G_f^{23}$ $[得到了G进行终止]$
$SK：S，d，e，p，h，b，a，q，r，f$
.

回溯：$G_f^{23}$，$f_r^{24}$，$r_q^{19}$，$q_h^{19}$，$h_e^{12}$，$e_d^9$，$d_s^{11}$，$S_{none}^{12}$
最终结果：$S\to d\to e\to h\to q\to r\to f\to G$

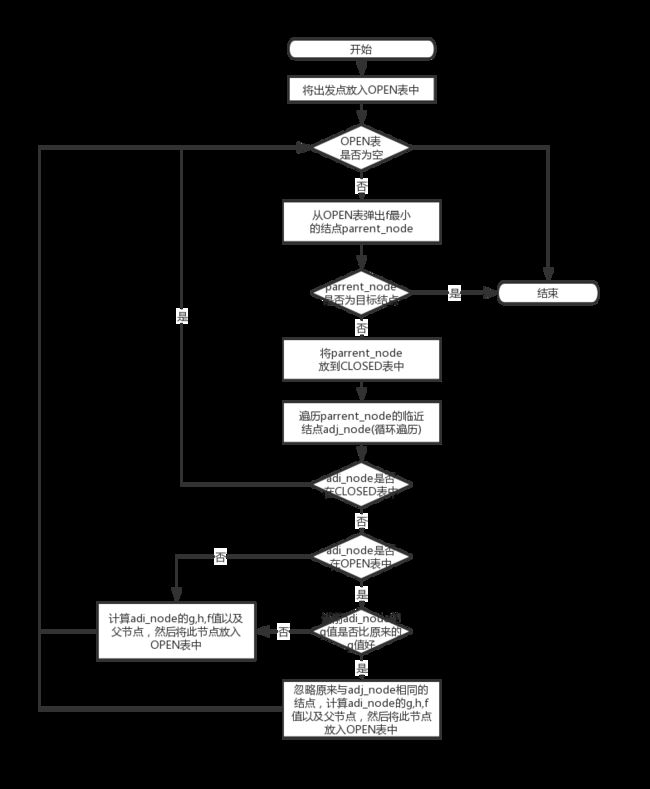
具体的实验过程中需要用某种数据结构来保存父节点，以便回溯，而且最终G结点的F值，就是实际路程。自我感觉良好，上面的那一段我输入了好长时间。不知道是什么原因，过程特别的卡顿，我猜是因为要解析好多的符号，可能需要消耗时间，比较少的时候还好，很多的话，就不如插入一张图片。这也是浏览器加载的时候需要注意的，加载一张图远比加载好多图来得快，所以会将好多图标都绘制在一张图上，在网页中只显示图片中的某一部分，这样一来，打开这样的网页，图片就只加载了一次。

流程图如下：

这是很久以前绘制的流程图，可能不是很准确但是是根据伪代码画出来的，应该不会有错。

伪代码：

4.算法源码

#!/usr/bin/python
# -*- coding: UTF-8 -*-
 
# redefine place
A = 0  # Arad
B = 1  # Bucharest
C = 2  # Craiova
D = 3  # Dobreta
E = 4  # Eforie
F = 5  # Fagaras
G = 6  # Giurgiu
H = 7  # Hirsova
I = 8  # Iasi
L = 9  # Lugoj
M = 10  # Mehadia
N = 11  # Neamt
O = 12  # Oradea
P = 13  # Pitesti
R = 14  # Rimnicu Vilcea
S = 15  # Sibiu
T = 16  # Timisoara
U = 17  # Urziceni
V = 18  # Vaslui
Z = 19  # Zerind

# 构建一个20*20的矩阵

PLACES_NUM = 20

# 地图
class Graph:
    def __init__(self):
        self.romania_graph = [[0] * PLACES_NUM for i in range(PLACES_NUM)]

    def add_edge(self, _from, _to, _value):
        if _from < PLACES_NUM:
            if _to < PLACES_NUM:
                self.romania_graph[_from][_to] = _value
                self.romania_graph[_to][_from] = _value

    def get_edge(self, _from, _to):
        return self.romania_graph[_from][_to]


#问题的最终解
class Stack:

    def __init__(self):
        self.stack = []

    def push(self, value):
        self.stack.append(value)
        return

    def pop(self):
        return self.stack.pop()

    def is_empty(self):
        if self.stack:
            return False
        return True

# CLOSED表
class Queue:
    def __init__(self):
        self.queue = []

    def put(self, value):
        self.queue.append(value)
        return

    def get(self):
        return self.queue.pop(0)

    def contain(self, value):
        return value in self.queue

    def is_empty(self):
        if self.queue:
            return False
        return True

# OPEN表
class PriorityQueue:

    def __init__(self):
        self.queue = []

    def put(self, node_cost):
        """
        :param node_cost: [value,cost]
        """
        self.queue.append(node_cost)

    def get(self):
        if self.queue:
            min_i = 0
            min_cost = self.queue[min_i][1]
            for i in range(len(self.queue)):
                if self.queue[i][1] < min_cost:
                    min_i = i
                    min_cost = self.queue[i][1]
            return self.queue.pop(min_i)

    def contain(self,value):
        for i in range(len(self.queue)):
            if self.queue[i][0]==value:
                return self.queue[i],True
        return None,False

    def is_empty(self):
        if self.queue:
            return False
        return True


# initialize undirected graph
# 初始化无向图
def init_graph():
    graph = Graph()

    graph.add_edge(O, Z, 71)
    graph.add_edge(O, S, 151)
    graph.add_edge(A, Z, 75)
    graph.add_edge(A, S, 140)
    graph.add_edge(A, T, 118)
    graph.add_edge(T, L, 111)
    graph.add_edge(L, M, 70)
    graph.add_edge(M, D, 75)
    graph.add_edge(D, C, 120)
    graph.add_edge(S, R, 80)
    graph.add_edge(S, F, 99)
    graph.add_edge(R, C, 146)
    graph.add_edge(F, B, 211)
    graph.add_edge(R, P, 97)
    graph.add_edge(C, P, 138)
    graph.add_edge(P, B, 101)
    graph.add_edge(B, G, 90)
    graph.add_edge(B, U, 85)
    graph.add_edge(U, H, 98)
    graph.add_edge(U, V, 142)
    graph.add_edge(V, I, 92)
    graph.add_edge(I, N, 87)
    graph.add_edge(H, E, 86)

    return graph


def a_star(graph, h, _root, _goal):
    g = [0] * PLACES_NUM  # g(n) value                          现阶段搜索过程中的每个结点的g(n)记录@
    parents = [0] * PLACES_NUM  # temporary parents             现阶段搜索过程中的每个节点的父结点记录@
    pq_open = PriorityQueue()  # open queue                     初始化open表@
    q_close = Queue()  # closed queue                           初始化closed表@
    s_path = Stack()  # solution nodes path                     s_path中作为走过路径记录@
    s_parent = Stack()  # solution nodes' parents path          s_parent中作为open表每次pop的记录@
    pq_open.put([_root, 0])                                     #将初始结点存入OPEN表中@
    
    while pq_open.is_empty()==False:
        parrent_node=pq_open.get()
        if parrent_node[0]==_goal:
            break
        q_close.put(parrent_node[0])
        for i in range(20):
            length=graph.get_edge(parrent_node[0],i)
            if length!=0:
                node,result=pq_open.contain(i)
                f=parrent_node[1]-h[parrent_node[0]]+length+h[i]
                if q_close.contain(i):
                    continue
                elif result==True:
                    if node[1]>f:
                        node.pop()
                        parents[i]=parrent_node[0]
                        pq_open.put([i,f])
                else:
                    parents[i]=parrent_node[0]
                    pq_open.put([i,f])
    path=[]
    cost=0
    print("parents:",parents)
    p=_goal

    while p!=_root:
        cost+=graph.get_edge(p,parents[p])
        path.append(p);
        p=parents[p]

    length=len(path)-1
    print('path:',_root,end='')
    for i in range(length+1):
        print(" -->",path[length-i],end='')
    print()
    return cost
    

if __name__ == '__main__':
    graph = init_graph()
    # 怎么才能够获取到这个矩阵
    h = (366, 0, 160, 242, 161,
         178, 77, 151, 226, 244,
         241, 234, 380, 98, 193,
         253, 329, 80, 199, 374)

    # place_str = input()
    # places = place_str.split()
    # cost = a_star(graph, h, eval(places[0]), eval(places[1]))

    print("node","A"," B")
    cost = a_star(graph, h,eval('A'),eval('B'))
    print('cost:',cost)
    print()
    print("node","C"," B")
    cost = a_star(graph, h,eval('C'),eval('B'))
    print('cost:',cost)
    print()
    print("node","U"," B")
    cost = a_star(graph, h,eval('U'),eval('B'))
    print('cost:',cost)
    print()

备注：

1. 保存好源码之后，自己多写几个print来看一看各个数据都是什么，避免超级低级的错误。
2. 源码总注释比较少，为何？因为有了流程图，以及上面的展示，A*算法的思想还是很容易就可以理解的，而且算法部分的代码很容易就能够看懂。
3. 话说我也不知道是为什么，我上传代码之后竟然没有高亮显示，感觉很奇怪，是不是我等级尚低，修为尚浅，还是因为之前的代码都是MATLAB代码。
4. 代码最后的部分，注释掉的三行是用来控制台输入的，但是鉴于Sublime Text3中input()函数不好用，我直接弄成了固定的测试数据。
5. 代码中最后的cost计算，可以直接从A*算法中得到，并不需要使用回溯的方法，所以我这里这样写，纯属画蛇添足，但是因为要输出路径，所以顺带算了一下 。

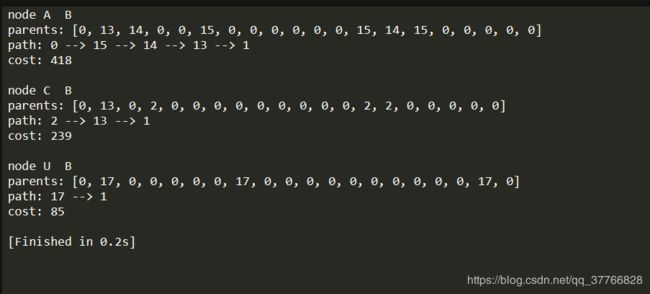
5.算法输出

6.总结

不难。但是却囿于有限的知识，而不能够将其进行扩展，A*算法是一种比较好的寻路算法，在游戏中会经常使用到，在Unity中有特定的寻路算法，也有一部分人是自己写的算法，自己写的话有什么好处呢？
倘若是自己写的寻路算法，在寻路的时候，可以给AI加上好多东西，这样可以让AI看上去不是那么傻？现在还是有一些疑惑的，寻路的时候是将地图当成了一个类似于坐标系一样的东西，中间遇到障碍物就会换路，而且是找到一条路径之后，AI才会出发，也就是说AI提前就知道一条路径，o( ￣︶￣ )o。
那么怎么把现在的这种数据跟游戏中寻路数据对应起来呢？好晕。找了一些个链接，有时间的时候可以看一看，或者就最近这一段时间看一看 。

链接如下：

1. A星算法详解(个人认为最详细,最通俗易懂的一个版本)
2. A* Pathfinding for Beginners(不用外网)
3. 堪称最好最全的A*算法详解（译文）
4. Amit’s A* Pages(不用外网)

应该尝试用各种编程语言写该算法，因为不能容忍自己的菜！！！