图论（4）：关键路径概念与算法（Graph实现）

概念

AOE网对应研究实际问题是工程的工期问题：（1）完成一项工程至少需要多少时间？（2）哪些活动是影响整个工程进度的关键？

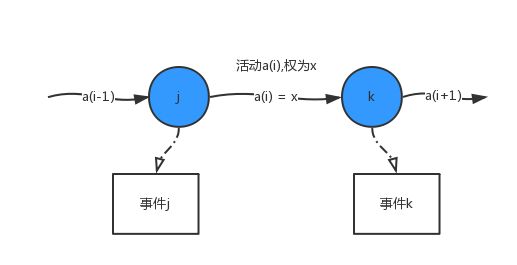
如果在有向图中用顶点表示事件，用弧表示活动，用弧上的权表示活动持续时间，则称该带权有向图(即有向网)为边表示活动的网(activity on edge network)，简称AOE网。如下图所示：

AOE网-活动与事件关系图

AOE网中的事件与活动有如下两个重要性质：
1、只有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始；
2、只有在进入某顶点的各活动都结束，该顶点所代表的事件才能发生。

由于一个工程只可能有一个开始点和一个完成点，故正常情况（无环）下，网中只可能有一个入度为0的节点（称为源点）和一个出度为0的节点（称为汇点）。

通常在一个工程中一些活动可以并行地进行，另一些活动则需要等待前面所有的活动完成后才能开始（因此，这里还涉及到事件的拓扑排序），所以完成整个工程的最短时间应该是从开始点到结束点的最长路径的长度（指的是活动持续时间之和，而非弧的数目）。路径长度最长的那条路径叫做关键路径，关键路径上的活动称为关键活动。因此，提前完成非关键活动并不能加快工程的进度。

与关键活动有关的量

如果我们用e(i)标识活动a(i)的最早开始时间，l(i)表示活动a(i)的最迟开始时间（这是在不推迟整个工程完成的前提下活动a(i)的最迟必须开始的时间），两者之差l(i) - e(i)意味着活动a(i)的时间余量。仅当活动a(i)满足条件l(i) == e(i)（即活动的时间余量为0）时表示为关键活动。

因此，要获得工程的关键路径就是找出满足条件l(i) == e(i)的所有活动（一个工程中可能存在多条关键路径）。

为了求得活动的e(i)和l(i)，首先应求得事件的最早发生时间ve(j)，和最迟发生时间vl(j)。如果活动a(i)由弧表示，其持续时间记为dut()，则满足如下关系式：
e(i) = ve(j)
l(i) = vl(k) - dut()

事件的最早发生时间ve(j)：是指从始点开始到顶点（事件）j的最大路径长度。这个长度决定了所有从顶点j出发的活动能够开工的最早时间。
从开始点往后递推求取：
ve(0) = 0; ve(j) = Max{ve(i) + dut() }, 其中∈T, j = 1, 2, ..., n -1; T为节点j的入度边集合。

事件最迟发生时间vl(j)：是指在不推迟整个工期的前提下,事件j允许的最晚发生时间。
从结束点往前递推求取：
vl(n - 1) = ve(n - 1); vl(i) = Min{vl(j) - dut()},其中∈S, i = n - 2, ..., 0; S为节点i的出度边集合。

示例

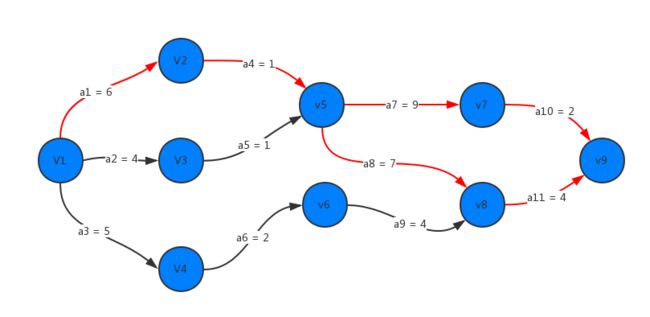
利用Guava的graph数据结构求得如下所示工程图的关键路径。graph的使用相关介绍请参考：图论（2）：Guava中Graph模块(wiki翻译)

关键路径示例图

1、构建示例图AOE网的数据结构：

MutableValueGraph graph = ValueGraphBuilder.directed()
    .nodeOrder(ElementOrder.insertion())
    .expectedNodeCount(10)
    .build();

graph.putEdgeValue(V1, V2, 6);
graph.putEdgeValue(V1, V3, 4);
graph.putEdgeValue(V1, V4, 5);
graph.putEdgeValue(V2, V5, 1);
graph.putEdgeValue(V3, V5, 1);
graph.putEdgeValue(V4, V6, 2);
graph.putEdgeValue(V5, V7, 9);
graph.putEdgeValue(V5, V8, 7);
graph.putEdgeValue(V6, V8, 4);
graph.putEdgeValue(V7, V9, 2);
graph.putEdgeValue(V8, V9, 4);
Log.i(TAG, "graph: " + graph);

输出：

nodes: [v1, v2, v3, v4, v5, v6, v7, v8, v9], 
edges: { v4>=5,  v2>=6,  v3>=4, 
 v5>=1,  v5>=1,  v6>=2,  v8>=7, 
 v7>=9,  v8>=4,  v9>=2,  v9>=4}

2、获取该有向图的拓扑排序列表：

/**
 * 利用Traverser接口将graph进行拓扑排序topologically，此处返回的逆拓扑排序
 */
Iterable topologicallys = Traverser.forGraph(graph)
        .depthFirstPostOrder(startNode);
Log.i(TAG, "topologically: " + format(topologicallys));

输出：

topologically: {v9,v8,v6,v4,v7,v5,v2,v3,v1} //这里是逆序

3、递推求得ve(j)值：

//获取ve(i)
Map ves = getVeValues(graph, topologicallys);
Log.i(TAG, "ves: " + format(ves));

/**
 * ve(j) = Max{ve(i) + dut() }; 属于T，j=1,2...,n-1
 * @param graph
 * @param topologicallys
 * @return
 */
private static Map getVeValues(ValueGraph graph, 
                                                Iterable topologicallys) {
    List reverses = Lists.newArrayList(topologicallys.iterator());
    Collections.reverse(reverses); //将逆拓扑排序反向
    Map ves = new ArrayMap<>(); //结果集
    //从前往后遍历
    for (String node : reverses) {
        ves.put(node, 0); //每个节点的ve值初始为0

        //获取node的前趋列表
        Set predecessors = graph.predecessors(node); 
        int maxValue = 0;
        
        //找前趋节点+当前活动耗时最大的值为当前节点的ve值
        for (String predecessor : predecessors) {
            maxValue = Math.max(ves.get(predecessor) +
                    graph.edgeValueOrDefault(predecessor, node, 0), maxValue);
        }
        ves.put(node, maxValue);
    }
    return ves;
}

输出：

ves: {v1:0, v2:6, v3:4, v4:5, v5:7, v6:7, v7:16, v8:14, v9:18}

4、递推求得vl(j)值：

/**
 * vl(i) = Min{vl(j) - dut(}; 属于S，i=n-2,...,0
 * @param graph
 * @param topologicallys
 * @param vels
 * @return
 */
private static Map getVlValues(ValueGraph graph,
    Iterable topologicallys, Map vels) {
    Map vls = new ArrayMap<>(); //结果集
    //从后往前遍历
    for (String node : topologicallys) {
        //获取node的后继列表
        Set successors = graph.successors(node);
        int initValue = Integer.MAX_VALUE; //初始值为最大值
        if (successors.size() <= 0) { //表示是结束点，赋值为ve值
            initValue = vels.get(node);
        }
        vls.put(node, initValue);
        int minValue = initValue;
        //找后继节点-当前活动耗时最少的值为当前节点的vl值
        for (String successor : successors) {
            minValue = Math.min(vls.get(successor) -
                    graph.edgeValueOrDefault(node, successor, 0), minValue);
        }
        vls.put(node, minValue);
    }
    return vls;
}

输出：

vls: {v1:0, v2:6, v3:6, v4:8, v5:7, v6:10, v7:16, v8:14, v9:18}

5、根据前面求取的ve(j)和vl(j)来找出关键活动（判断条件：ve(j) == vl(k) - dut()）：

/**
 * 判断条件：ve(j) == vl(k) - dut()
 */
//关键活动结果集
List> criticalActives = new ArrayList<>(); 
//返回图中所有活动(边)
Set> edgs = graph.edges(); 
//遍历每一条边（活动），过滤出：ve(j) == vl(k) - dut
for (EndpointPair endpoint : edgs) {
    final int dut = graph.edgeValueOrDefault(endpoint.nodeU(), endpoint.nodeV(), 0);
    //ve(j) == vl(k) - dut
    if (vls.get(endpoint.nodeV()) - dut == ves.get(endpoint.nodeU())) { 
        criticalActives.add(endpoint);
    }
}
Log.i(TAG, "critical actives: " + format(criticalActives));

输出：

critical actives: { v2>,  v5>,  v8>,  v7>,
 v9>,  v9>}

从输出可知，图中存在两条关键路径：{ v2>, v5>, v8>, v9>} 和 { v2>, v5>, v7>, v9>}(在示例图中使用红色线段标注)。因此，缩短这两条路径上活动的工期，将能有效的缩短整个工程的工期。
关键路径详细代码参见Demo：GH-Demo-CriticalPath。

参考文档

https://www.cnblogs.com/hongyang/p/3407666.html