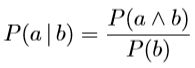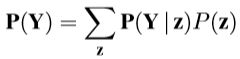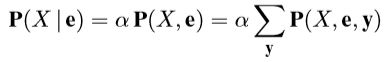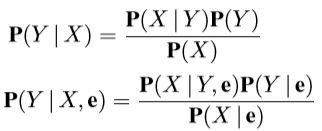Quantifying Uncertainty
Acting under Uncertainty
Qualification Problem: There is no complete solution within logic, system designers have to use good judgment in deciding how detailed that want to be in specifying their model, and what details they want to leave out.
Rational Decision: The right thing to do depends on both the relative importance of various goals and the likelihood that, and degree to which, they will be achieved.
Summary of Uncertainty
Probability provides a way of summarizing the uncertainty that comes from our laziness and ignorance, thereby solving the qualification problem.
The method of probability theory gives out a probability from 0 to 1 for each situation under any given state, rather than a positive judgment.
Uncertainty and Rational Decisions
To make choice, an agent must first have preferences between the different possible outcomes of various plans. Utility theory is used to represent and reason with preferences. The utility of a state is relative to an agent.
As expressed by utilities, preferences are combined with probabilities in the general theory of rational decisions called decision theory:
Decision Theory = Probability Theory + Utility Theory
Maximum Expected Utility (MEU) is the fundamental idea of decision theory, which means that an agent is rational if and only if it chooses the action that yields the highest expected utility, averaged over all the possible outcomes of the action.
Basic Probability Notation
What Probabilities Are About
The possible worlds are mutually exclusive and exhaustive which means that two possible worlds cannot both be the case, and one possible world must be the case.
- unconditional probability/prior probability: probabilities that don’t have some given conditions
- conditional probability/posterior probability: probabilities that have some given conditions
conditional probabilities are defined in terms of unconditional probabilities as follows:
for any propositions a and b:
written in a different form called the product rule*
Propositions in Probability Assertions
Variables in probability theory are called random variables and every random variable has a domain which means the set of possible values it can take on.
Probability distribution: the probabilities defined on the variables. (mostly for discrete distributions)
Probability density function (pdf): the probabilities distributed on a set of continuous variables
- Joint probability distribution: the distribution of multiple variables perform in the same time
- Marginal probability distribution: the distribution of one of all the variables performs
Probability Axioms
- The probability of a proposition plus the probability of its negation equals 1.
- Inclusion-exclusion principle:
Inference Using Full Joint Distributions
- marginalization
- conditioning
Supposed that there is a single variable X, let E be the list of evidence variables, let e be the list of observed values for them and Y be the remaining unobserved variables. Given all of these conditions, there is the following equation:
Independence
Independence/marginal independence/absolute independence between variables X and Y can be written as follows:
If the complete set of variables can be divided into independent subsets, then the full joint distribution can be factored into separate joint distributions on those subsets.
Conditional independence between two variables X and Y, given a third variables Z, can be written as follows:
Bayes’ Rule
Bayes’ rule/Bayes’ law/Bayes’ theorem
Supposed that all of the variables are mutually independent, then we can get the naïve Bayes model, which is always used to classify (naïve Bayes classifier)
Naïve Bayes Classifier on wiki:
https://en.wikipedia.org/wiki/Naive_Bayes_classifier
Please indicate the source of the reference. This article will be updated permanently:https://blogs.littlegenius.xin/2020/01/17/Uncertainty-0/