计算机视觉:图像滤波
图像滤波
- 空间域中的图像滤波
- 滤波是像素矩阵的数学运算。
- 平滑、锐化、测量纹理
- 频域中的图像滤波
- 滤波是修改图像频率的一种方法。
- 去噪、采样、图像压缩
- 图像金字塔
- 尺度空间表示允许粗到细的操作
计算每个位置的局部邻域函数。
线性滤波和非线性滤波:
滤波的意思就是对原图像的每个像素周围一定范围内的像素进行运算,运算的范围就称为掩膜或领域。而运算就分两种了,如果运算只是对各像素灰度值进行简单处理(如乘一个权值)最后求和,就称为线性滤波;而如果对像素灰度值的运算比较复杂,而不是最后求和的简单运算,则是非线性滤波;如求一个像素周围3x3范围内最大值、最小值、中值、均值等操作都不是简单的加权,都属于非线性滤波。
低通滤波和高通滤波:
低通滤波器由于滤掉了高频成分,高频成分含有大量边缘信息,所以造成了一定程度的图像模糊。高通滤波器滤掉了低频成分,保留了高频成分,即保留了边界信息,所以显示出原图像的边界。边缘检测是高通滤波,高斯模糊是低通滤波。
图像的频域处理_低通滤波和高通滤波
线性滤波
- BoxFilter
它做了什么?
- 将每个像素替换为其邻域的平均值。
- 达到平滑效果(去除锐利特征)。
对于滤波器,也有一定的规则要求:
- 滤波器的大小应该是奇数,这样它才有一个中心,例如3x3,5x5或者7x7。有中心了,也有了半径的称呼,例如5x5大小的核的半径就是2。
- 滤波器矩阵所有的元素之和应该要等于1,这是为了保证滤波前后图像的亮度保持不变。当然了,这不是硬性要求了。如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但也会非常暗。
- 对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
图像滤波的用途:
-
增强图像
- 去噪、调整大小、增加对比度等。
-
从图像中提取信息
- 纹理、边缘、特征点等。
-
检测模式
- 模板匹配。
-
向左移动1像素
- 垂直边缘(绝对值)
- 水平边缘(绝对值)
- 锐化滤波器:强调与周围平均水平的差异
相关和卷积
相关和卷积都是线性的、移位不变的。当滤波器对称时,相关和卷积是相同的。
- 线性滤波的性质:线性,位移不变性;任何线性的、移位不变的算子都可以表示为卷积。
- 卷积的性质:交换律,结合律,分配律,数乘结合律。
- 滤波后的图像大小不变。
- 卷积会先反转卷积核,卷积操作会改变图像大小。
图像处理中滤波(filtering)与卷积(convolution)的区别
卷积与滤波、相关的区别,以及imfilter函数、conv2函数的介绍
高斯滤波和可分离核
- 高斯核的可分离性
- 可分离性示例
- 加速比
高斯经验法则:将滤波器半径设置为约3σ。
靠近边缘的像素如何处理?(边缘效应)
- 使用常数填充(例如,0)
- 复制边缘像素
中值滤波
中值滤波是一种非线性数字滤波器技术,经常用于去除图像或者其它信号中的噪声。
中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术,中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替,让周围的像素值接近的真实值,从而消除孤立的噪声点。
中值滤波是跟均值滤波唯一不同是,不是用均值来替换中心每个像素,而是将周围像素和中心像素排序以后,取中值。
均值滤波和中值滤波的内容非常基础,均值滤波相当于低通滤波,有将图像模糊化的趋势,对椒盐噪声基本无能为力。中值滤波的优点是可以很好的过滤掉椒盐噪声,缺点是易造成图像的不连续性。
中值滤波不是一种卷积。
中值滤波与均值滤波各自的优缺点
均值滤波,中值滤波,最大最小值滤波
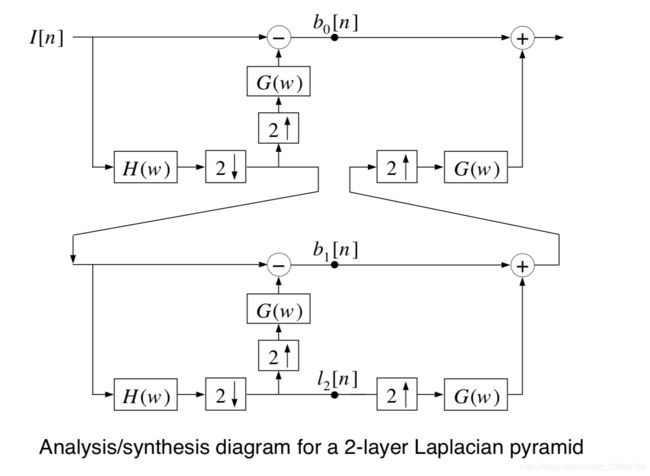
图像金字塔
% 确定高斯模糊核
h=[1,4,6,4,1]/16;
function [new_img]=getPyDown(img,h)
% 高斯模糊
temp = imfilter(img,h,'conv','same','replicate');
temp = imfilter(temp,h','conv','same','replicate');
% 下采样
new_img = temp(1:2:end,1:2:end,:);
end
function [new_img]=getPyUp(img,h)
% 上采样
temp = imresize(img,2,'bilinear');
% 高斯模糊
temp = imfilter(temp,h,'conv','same','replicate');
new_img = imfilter(temp,h','conv','same','replicate');
end
function [Gau,Lapla]=getPyramids(img,h)
nums = 4;
Gau = cell(nums,1);
N =1;
% 原图进高斯金字塔最底层
Gau{N} = img;
% ------------------------生成高斯金字塔-------------------------------%
for N = 2:nums
Gau{N} = getPyDown(Gau{N-1},h);
end
% -------------------生成拉普拉斯金字塔-----------------------------------%
Lapla = cell(nums-1,1);
for index = nums-1:-1:1
temp = getPyUp(Gau{index+1},h);
Lapla{index} = Gau{index} -temp;
end
end
- 二层拉普拉斯的合成图
拉普拉斯金字塔的用途:
- 图像压缩
- 图像恢复
- 图像融合
- 图像增强
双边滤波
双边滤波是一种非线性滤波器,它可以达到保持边缘、降噪平滑的效果。和其他滤波原理一样,双边滤波也是采用加权平均的方法,用周边像素亮度值的加权平均代表某个像素的强度,所用的加权平均基于高斯分布。最重要的是,双边滤波的权重不仅考虑了像素的欧氏距离(如普通的高斯低通滤波,只考虑了位置对中心像素的影响),还考虑了像素范围域中的辐射差异(例如卷积核中像素与中心像素之间相似程度、颜色强度,深度距离等),在计算中心像素的时候同时考虑这两个权重。
双边滤波里的两个权重域的概念:空间域(spatial domain S)和像素范围域(range domain R),这个是它跟高斯滤波等方法的最大不同点。
Bilateral Filters(双边滤波算法)原理及实现
双边滤波的核函数是空间域核与像素范围域核的综合结果:在图像的平坦区域,像素值变化很小,对应的像素范围域权重接近于1,此时空间域权重起主要作用,相当于进行高斯模糊;在图像的边缘区域,像素值变化很大,像素范围域权重变大,从而保持了边缘的信息。
- 空间 σs : 核的空间范围,考虑的邻域的大小。
- 范围 σr : 边缘的“最小”振幅。
只考虑空间和范围都接近的像素。
- 双边滤波器的参数选择
- 空间参数:与图像大小成比例。
- 例如,图像对角线的2%。
- 范围参数:与边缘振幅成比例。
- 例如,图像梯度的平均值或中间值。
双边滤波器穿过细线:迭代
双边滤波器难以实现
- 非线性。
- 复杂的,空间变化的核。
- 不能预先计算,没有fft(快速傅里叶变换)。
- 蛮力执行速度慢。