Autoencoder(自编码器)
自编码器原理:
在神经网络中是监督学习下的操作,那么它又如何应用到无监督学习中呢?一个直观的想法就是让经过了神经网络的输入等于元输入,或者尽量相差不大。这样做不就可以学习到输入数据中隐含着某些特定的结构,甚至通过设计神经元数目来完成数据压缩吗?自编码器由一个编码器(encoder)函数和一个解码器(decoder)函数组合而成。编码器函数将输入数据转换为一种不同的表示,而解码器函数则将这个新的表示转换到原来的形式,尽可能复现输入信号的神经网络,而为了实现这种复现,自动编码器就必须自动捕捉可以代表输入数据的最重要的因素。
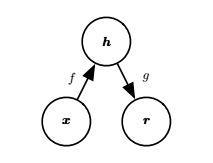
编码器 f f f 将 x x x 映射到 h h h,解码器 g g g 将 h h h 映射到 r r r。 r r r 和 x x x 应尽可能的相似。当然了,度量这个相似度,需要一个损失函数,根据解码器的不同,损失函数可以有多种取法,比如如果是恒等函数可取平方误差: L ( x , y ) = ∣ ∣ x − r ∣ ∣ 2 L(x,y)=||x-r||^2 L(x,y)=∣∣x−r∣∣2如果是为Sigmoid函数则取交叉熵 L ( x , r ) = − ∑ i = 1 n [ x i l o g ( r i ) + ( 1 − x i ) l o g ( 1 − r i ) ] L(x,r)=-\sum\limits_{i=1}^n [x_ilog(r_i)+(1-x_i)log(1-r_i)] L(x,r)=−i=1∑n[xilog(ri)+(1−xi)log(1−ri)]
最小化这个函数即可得到相似的 r r r 了,但是它目前只是学到了一个好的特征,能在最大程度上代替原数据。如果是为了实现分类,那么可以在自动编码器的最顶层添加一个分类器(逻辑回归,SVM等),然后通过标准的多层神经网络的监督训练(梯度下降)去训练。这样做能使分类效果得到很大的提升。
如果编码器直接就学习到r=x怎么办?自编码器的变体们
稀疏自动编码器(Sparse AutoEncoder):SA是在自动编码器的基础上,加入了L1正则化的限制,这样可以让每次得到的code尽量稀疏,至于为什么…因为稀疏的表达往往比其他的表达要有效(人脑也是这样,某个输入只会刺激某些神经元(1%~4%),其他大部分的神经元是收到抑制的)。所以此时的损失函数J为:
J = ∑ L ( x , r ) + α ∑ i , j W i , j 2 , 其 中 W 是 权 重 矩 阵 J=\sum L(x,r)+\alpha\sum\limits_{i,j}W_{i,j}^2,其中W是权重矩阵 J=∑L(x,r)+αi,j∑Wi,j2,其中W是权重矩阵
降噪自动编码器(Denoising AutoEncoders):DA是在自动编码器的基础上,在训练的数据中加入了噪声,这样做可以让自动编码器必须学习去如何去除这种噪声来获得真正的没有被噪音污染过的输入,使得到的结果泛化能力强。
稀疏编码(Sparse Coding):自编码器的目的是有效的找出隐含的数据内部的结构和模式,参考人大脑的神经元其实只对某些“重点”感兴趣,比如在图像中的边缘,所以“稀疏”是很必要的手段。首先如果把输出必须和输入必须相等的限制放松,同时利用线性代数中基的概念,使: x = ∑ i = 1 k a i ϕ i x=\sum\limits_{i=1}^k a_i\phi_i x=i=1∑kaiϕi
其中a系数表示的是输入样本的特征。那么问题就变成了寻找一组最好的基。而一般情况下要求基的个数k非常大,甚至一般情况下要比n大很多,所以将导致a系数不能唯一确定。所以需要对系数a作稀疏性约束,此时系统对应的损失函数为: m i n i m i z e a i j , ϕ i ∑ j = 1 n ∣ ∣ x j − ∑ i = 1 k a i ( j ) ϕ i ∣ ∣ 2 + α ∑ i = 1 k S ( a i ( j ) ) minimize_{a_i^{j},\phi_i} \sum\limits_{j=1}^n ||x^{{j}}-\sum\limits_{i=1}^k a_i^{(j)}\phi_i||^2+\alpha\sum\limits_{i=1}^kS(a_i^{(j)}) minimizeaij,ϕij=1∑n∣∣xj−i=1∑kai(j)ϕi∣∣2+αi=1∑kS(ai(j))
同时还对基也进行限制,让 ∣ ∣ ϕ i ∣ ∣ 2 ||\phi_i||^2 ∣∣ϕi∣∣2小于等于C,这样才能使矩阵更加的稀疏。再优化这个损失函数,由于有a和 ϕ \phi ϕ两个变量,可以运用EM的思想,即先固定 ϕ \phi ϕ,调整a,是损失函数最小(由于加了正则化,即解LASSO问题);然后固定a,调整 ϕ \phi ϕ,使损失函数最小(凸优化问题),不断迭代,最后能得到一组很好的基了。

这张图会更加的清晰,而且中间层是可以任由我们自己设计与控制的。
def fit(self, n_dimensions):
graph = tf.Graph()
with graph.as_default():
# 输入X
X = tf.placeholder(self.dtype, shape=(None, self.features.shape[1]))
#初始化权重
encoder_weights = tf.Variable(tf.random_normal(shape=(self.features.shape[1], n_dimensions)))
encoder_bias = tf.Variable(tf.zeros(shape=[n_dimensions]))
decoder_weights = tf.Variable(tf.random_normal(shape=(n_dimensions, self.features.shape[1])))
decoder_bias = tf.Variable(tf.zeros(shape=[self.features.shape[1]]))
# Encoder
encoding = tf.nn.sigmoid(tf.add(tf.matmul(X, encoder_weights), encoder_bias))
# Decoder
predicted_x = tf.nn.sigmoid(tf.add(tf.matmul(encoding, decoder_weights), decoder_bias))
#损失函数
cost = tf.reduce_mean(tf.pow(tf.subtract(predicted_x, X), 2))
optimizer = tf.train.AdamOptimizer().minimize(cost)
with tf.Session(graph=graph) as session:
# Initialize global variables
session.run(tf.global_variables_initializer())
for batch_x in batch_generator(self.features):
self.encoder['weights'], self.encoder['bias'], _ = session.run([encoder_weights, encoder_bias, optimizer],
feed_dict={X: batch_x})
def reduce(self):
return np.add(np.matmul(self.features, self.encoder['weights']), self.encoder['bias'])
编码器只是一个思想大概,而真正的应用才刚刚开始,如变分自编码器:https://blog.csdn.net/qq_39388410/article/details/79129197 等更多的生成模型。