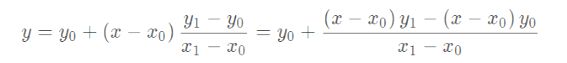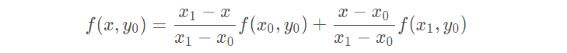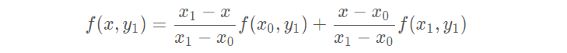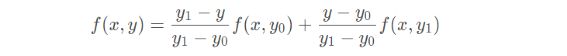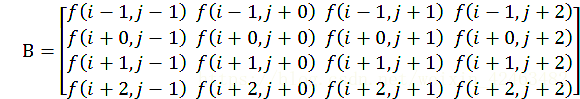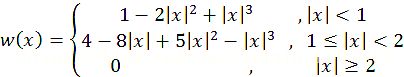【图像处理】详解 最近邻插值、线性插值、双线性插值、双三次插值
目录
一、绪论
二、说明
2.1 最近邻插值 (Nearest Neighbor Interpolation) —— 零阶插值法
2.2 线性插值 (Linear Interpolation) —— 一阶插值法
2.3 双线性插值 (Bilinear Interpolation) —— 一阶插值法
2.4 双三次插值 (Bicubic Interpolation)
三、比较与总结
四、更多
一、绪论
插值 (Interpolation),通常指内插,既是离散数学名词,也是图像处理术语,二者的联系十分密切。作为图像放缩 (Scale) 的手段,常见的传统插值方法有:最近邻插值 (Nearest Neighbour Interpolation)、线性插值(Linear Interpolation)、双线性插值 (Bilinear Interpolation)、双三次插值 (Bicubic interpolation) 等乃至更高阶的线性插值方法。
在离散数学中,插值指在离散数据的基础上补插连续函数,使得连续曲线通过全部给定的离散数据点。作为离散函数逼近的重要方法,利用插值可根据函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
这实际指出了插值的本质 —— 利用已知数据估计未知位置数值。图像插值问题类似于拟合问题,二者均为函数逼近或数值逼近的重要组成部分。但不同之处在于,对于给定的函数,插值要求离散点“坐落在”函数曲线上从而满足约束;而拟合则希望离散点尽可能地“逼近”函数曲线。
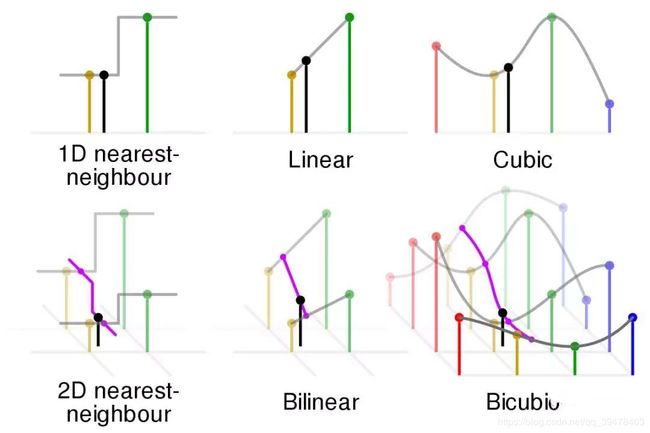
至于为什么要插值,上图展示了一个二维图像/像素坐标系下,数字图像放大3倍的局部坐标点变换。对于原图像的坐标点 (红色实心点),其在新图像上都能确定一一对应的坐标点 (红色实心点)。而对于新图像中因放大而的多出坐标点 (蓝色圈叉),则在原图像中找不到对应点了,这可如何是好呢?这时,插值技术应运而生,旨在通过某些规则/规范/约束,获取这些多出坐标点的像素值。举个简单的一维例子:
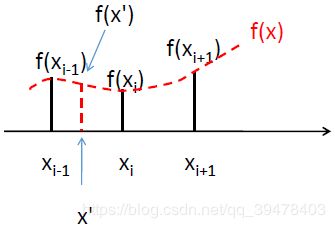
如上图所示,假设数轴上某三个离散点坐标分别为 xi-1,xi,xi+1。对于给定某连续函数 f(x) 作为约束条件/规则,三点坐标的函数值分别为 f(xi-1),f(xi), f(xi+1)。这时,如果我们想得到更密集、更精细的点,则可以给定坐标值,根据 f(x) 得到函数值。例如,设 xi-1 和 xi 之间的一坐标点 x',根据 f(x) 其函数值即为 f(x')。
上例即为一个简易的一维插值表示,f(x') 就是一个插值结果。事实上,给定不同的函数约束 f(x),通常会得到不同的插值结果,因此当前存在多种不同的插值方法,而本文将结合图示逐一说明这些传统的线性插值原理。
二、说明
2.1 最近邻插值 (Nearest Neighbor Interpolation) —— 零阶插值法
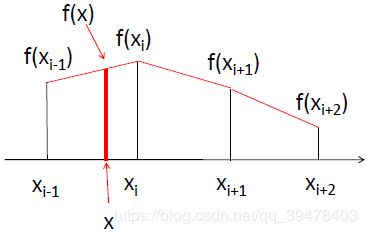
上图是一个一维的最近邻插值的示意图,坐标轴上各点 xi-1,xi,xi+1 ... 两两对半等分间隔 (红色虚线划分),从而非边界的各坐标点都有一个等宽的邻域,并根据每个坐标点的值构成一个类似分段函数的函数约束,从而使各插值坐标点的值等同于所在邻域原坐标点的值。例如,插值点 x 坐落于 坐标点 xi 的邻域,那么其值 f(x) 就等于 f(xi)。
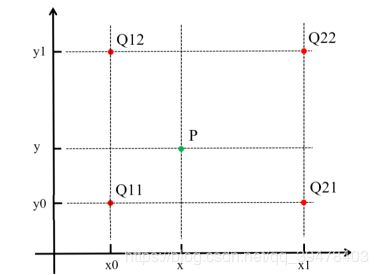
上图是一个二维最近邻插值的定量俯视示意图,(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) 都是原图像上的坐标点,灰度值分别对应为 Q11、Q12、Q21、Q22。而灰度值未知的插值点 (x, y),根据最近邻插值方法的约束,其与坐标点 (x0, y0) 位置最接近 (即位于 (x0, y0) 的邻域内),故插值点 (x, y) 的灰度值 P = Q11。
了解机器学习 KNN (K - Nearest Neighbor) 分类算法的人会知道,这其实等同于 K=1 的 1NN。
2.2 线性插值 (Linear Interpolation) —— 一阶插值法
上图是一个一维的线性插值的定性示意图,坐标轴上各点 xi-1,xi,xi+1 ... 的值“两两直接相连”为线段,从而构成了一条连续的约束函数。而插值坐标点例如 x,根据约束函数其值应为 f(x)。因为每两个坐标点之间的约束函数曲线是一次线性的线段,对插值结果而言是“线性” 的,所以该方法称为线性插值。
上图是一个一维线性插值的定量示意图,x0 和 x1 都是原有的坐标点,灰度值分别对应为 y0 和 y1。而灰度值未知的插值点 x,根据线性插值法约束,在 (x0, y0) 和 (x1, y1) 构成的一次函数上,其灰度值 y 即为:
实际上,即便 x 不在 x0 与 x1 之间,该公式也成立,但此时这种方法叫线性外插。
2.3 双线性插值 (Bilinear Interpolation) —— 一阶插值法
由一维的线性插值很容易拓展到二维图像的双线性插值,每次需要要经过三次一阶线性插值才能获得最终结果,上图便展示了该过程的一种定性斜视示意图。其中,(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) 均为原图像上的像素坐标点,灰度值分别对应为 f(x0, y0)、f(x0, y1)、f(x1, y0)、f(x1, y1)。而灰度值未知的插值点 (x, y),根据双线性插值法的约束,可以先由像素坐标点 (x0, y0) 和 (x0, y1) 在 y 轴向作一维线性插值得到 f(x0, y)、由像素坐标点 (x1, y0) 和 (x1, y1) 在 y 轴向作一维线性插值得到 f(x1, y),然后再由 (x0, y) 和 (x1, y) 在 x 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y)。当然,一维线性插值先作 x 轴向再作 y 轴向,得到的结果完全相同,仅为顺序先后的区别,例如:
上图是一个二维双线性插值的定量俯视示意图 (点位稍有变动但不影响),我们换个顺序。先由像素坐标点 (x0, y0) 和 (x1, y0) 在 x 轴向作一维线性插值得到 f(x, y0)、由像素坐标点 (x0, y1) 和 (x1, y1) 在 x 轴向作一维线性插值得到 f(x, y1):
然后再由 (x, y0) 和 (x, y1) 在 y 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y):
合并上式,得到最终的双线性插值结果:
2.4 双三次插值 (Bicubic Interpolation)
又称立方卷积插值/双立方插值,在数值分析中,双三次插值是二维空间中最常用的插值方法。在这种方法中,插值点 (x, y) 的像素灰度值 f(x, y) 通过矩形网格中最近的十六个采样点的加权平均得到,而各采样点的权重由该点到待求插值点的距离确定,此距离包括水平和竖直两个方向上的距离。相比之下,双线性插值则由周围的四个采样点加权得到。
上图是一个二维图像的双三次插值俯视示意图。设待求插值点坐标为 (i+u, j+v),已知其周围的 16 个像素坐标点 (网格) 的灰度值,还需要计算 16 个点各自的权重。以像素坐标点 (i, j) 为例,因为该点在 y 轴和 x 轴方向上与待求插值点 (i+u, j+v) 的距离分别为 u 和 v,所以的权重为 w(u) × w(v),其中 w(·) 是插值权重核 (可以理解为定义的权重函数)。同理可得其余 15 个像素坐标点各自的权重。那么,待求插值点 (i+u, j+v) 的灰度值 f(i+u, j+v) 将通过如下计算得到:
![]()
其中各项由向量或矩阵表示为:
![]()
![]()
插值权重核 w(·) 为:
其函数图像如下所示:
三、比较与总结
插值算法常用于对图像进行缩放处理。数字图像像素的灰度值是离散的,因此一般的处理方法是对原来在整数点坐标上的像素值进行插值生成连续的曲面,然后在插值曲面上重新采样以获得缩放图像像素的灰度值。缩放处理从输出图像出发,采用逆向映射方法,即在输出图像中找到与之对应的输入图像中的某个或某几个像素,从而保证输出图像中的每个像素都有一个确定值。否则,若从输入图像出发来推算输出图像,输出图像的像素点可能出现无灰度值的情况。因为对图像进行缩放处理时,输出图像像素和输入图像之间可能不再有一一对应关系。实际应用中,常利用插值技术增加图形数据,以便在打印或以其他形式输出时,能够增大打印面积及 (或) 分辨率。
最近邻插值 法的优点是计算量很小,算法也简单,因此运算速度较快。但它仅使用离待测采样点最近的像素的灰度值作为该采样点的灰度值,而没考虑其他相邻像素点的影响,因而重新采样后灰度值有明显的不连续性,图像质量损失较大,会产生明显的马赛克和锯齿现象。
双线性插值 法效果要好于最近邻插值,只是计算量稍大一些,算法复杂些,程序运行时间也稍长些,但缩放后图像质量高,基本克服了最近邻插值灰度值不连续的特点,因为它考虑了待测采样点周围四个直接邻点对该采样点的相关性影响。但是,此方法仅考虑待测样点周围四个直接邻点灰度值的影响, 而未考虑到各邻点间灰度值变化率的影响, 因此具有低通滤波器的性质, 从而导致缩放后图像的高频分量受到损失, 图像边缘在一定程度上变得较为模糊。用此方法缩放后的输出图像与输入图像相比, 仍然存在由于插值函数设计考虑不周而产生的图像质量受损与计算精度不高的问题。
双三次插值 法计算量最大,算法也是最为复杂的。在几何运算中,双线性内插法的平滑作用可能会使图像的细节产生退化,在进行放大处理时,这种影响更为明显。在其他应用中,双线性插值的斜率不连续性会产生不希望的结果。立方卷积插值不仅考虑到周围四个直接相邻像素点灰度值的影响,还考虑到它们灰度值变化率的影响。因此克服了前两种方法的不足之处,能够产生比双线性插值更为平滑的边缘,计算精度很高,处理后的图像像质损失最少,效果是最佳的。
总之,在进行图像缩放处理时,应根据实际情况对三种算法做出选择,既要考虑时间方面的可行性,又要对变换后图像质量进行考虑,这样才能达到较为理想的结果。
四、更多
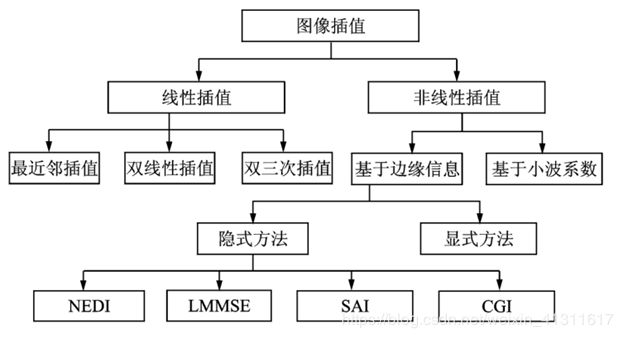
事实上,当前的插值技术还有很多,如上图所示,大致可分为两类:一是 线性插值 方法,二是 非线性插值 方法。
一方面,传统插值方法多为 线性插值 方法,如最近邻插值、双线性插值、双三次插值等。这类方法在插值过程中采用同一种插值内核、无需考虑待插像素点所处位置,以至于图像中的高频部分 —— 边缘纹理等变得模糊,无法达到高清效果。
另一方面,非线性插值 方法主要有:基于 小波系数 的方法和基于 边缘信息 的方法。其中,基于边缘信息的方法又可分为 隐式方法 和 显式方法。隐式方法含:边缘导向插值 (New edge directive interpolation,NEDI)、最小均方误差估计插值 (Linear minimum mean square-error estimation,LMMSE)、软判决自适应插值 (Soft-decision adaptive interpolation interpolation, SAI),边缘对比度引导图像插值 (Contrast-guided image interpolation, CGI) 等均为基于图像边缘的隐式插值方法。
此外,还有更后来发展的诸如基于 决策树、字典学习、深度学习 等的图像插值算法。
赠人玫瑰,手有余香~ 如果觉得有帮助,请为我点个赞吧 ~
参考文献:
《数字图像处理》- 冈萨雷斯
https://baike.baidu.com/item/插值/13014727
https://baike.baidu.com/item/插值/1196063?fr=aladdin
https://www.jianshu.com/p/92b5619e7b4b
http://blog.chinaaet.com/justlxy/p/5100052699
https://blog.csdn.net/weixin_42463482/article/details/82830628
https://www.cnblogs.com/okaimee/archive/2010/08/18/1802585.html
https://blog.csdn.net/weixin_41311617/article/details/88943092