小波变换和小波包变换

一、小波变换

1、连续型小波变换

小波变换是一个平方可积函数 f(t) f ( t ) 与一个时频域上具有良好局部性质的小波函数 ψ(t) ψ ( t ) 的内积：

Wf(a,b)=<f,ψa,b>=1a−−√ψ∗(t−ba)dt W f ( a , b ) =< f , ψ a , b >= 1 a ψ ∗ ( t − b a ) d t

式中， <∗,∗> < ∗ , ∗ > 表示内积； b b 为位移因子； ∗ ∗ 表示复数共轭； ψa,b(t) ψ a , b ( t ) 为

ψa,b(t)=1a−−√ψ(t−ba) ψ a , b ( t ) = 1 a ψ ( t − b a )

式中， ψa,b(t) ψ a , b ( t ) 是母小波 ψ(t) ψ ( t ) 经位移和伸缩所产生的一族函数，称为小波基函数或简称小波基。

由上式可以看到，改变 a a 值，对函数 ψa,b(t) ψ a , b ( t ) 具有伸展 (a>1) ( a > 1 ) 或收缩 (a<1) ( a < 1 ) 的作用；改变 b b ，则会影响函数 f(t) f ( t ) 围绕 b b 点的分析结果。
ψ(t) ψ ( t ) 必须满足容许性条件：

∫∞−∞ψ(t)dt=0 或 ∫∞−∞|Ψ(ω)|2|ω|dω=Cψ<∞ ∫ − ∞ ∞ ψ ( t ) d t = 0   或   ∫ − ∞ ∞ | Ψ ( ω ) | 2 | ω | d ω = C ψ < ∞

式中， Ψ(ω) Ψ ( ω ) 是 ψ(t) ψ ( t ) 的傅里叶变换。
由上式可以得出， ψ(t) ψ ( t ) 的时域波形具有“衰减性”和“波动性”，即其振幅具有正负相间的振荡；从频谱上看， Ψ(ω) Ψ ( ω ) 集中在一个“小”的频带内，具有“带通性”。
ψa,b(t) ψ a , b ( t ) 中参数 a a 的伸缩和参数 b b 的平移为连续取值的小波变换称为连续小波变换，连续小波变换主要用于理论分析方面。

2、离散型小波变换

在实际应用中，需要对尺度因子 a a 和位移因子 b b 进行离散化处理，可以取：

a=am0,b=nb0am0 a = a 0 m , b = n b 0 a 0 m

式中， m,n m , n 为整数； a0 a 0 为大于1的常数； b0 b 0 为大于0的常数； a a 和 b b 的选取与小波 ψ(t) ψ ( t ) 的具体形式有关。
离散小波函数表示为

ψm,n(t)=1am0−−−√ψ(t−nb0am0am0)=1am0−−−√ψ(a−m0t−nb0) ψ m , n ( t ) = 1 a 0 m ψ ( t − n b 0 a 0 m a 0 m ) = 1 a 0 m ψ ( a 0 − m t − n b 0 )

相应的离散小波变换表示为

Wf(m,n)=<f,ψm,n(t)>=∫+∞−∞f(t)ψ∗m,n(t)dt W f ( m , n ) =< f , ψ m , n ( t ) >= ∫ − ∞ + ∞ f ( t ) ψ m , n ∗ ( t ) d t

特别的，当 a0=2,b0=1 a 0 = 2 , b 0 = 1 时，离散小波变换称为二进离散小波变换。这种二进离散小波变换简单方便没在实际时间序列处理中被广泛应用。

二、小波包变换

1、小波包

小波包的介绍参考：https://baike.baidu.com/item/%E5%B0%8F%E6%B3%A2%E5%8C%85/19065272?fr=aladdin

2、小波包对时间序列的分解特性

小波分析是把时间序列 S S 分解成低频信息 a1 a 1 和高频信息 d1 d 1 两部分，在分解中 ，低频 a1 a 1 中失去的信息由高频 d1 d 1 捕获。在下一层的分解中，又将 a1 a 1 分解成低频 a2 a 2 和高频 d2 d 2 两部分，低频 a2 a 2 中失去的信息由高频 d2 d 2 捕获。依此类推，可以进行更深层的分解。小波包分解不仅对低频部分进行分解，而且还对高频部分进行分解。因此，小波包分解是一种更广泛应用的小波分解方法，应用于信号的分解、编码、消噪、压缩等方面。

三、小波包算法

下面介绍小波包的分解算法和重构算法。
设 gnj(t)∈Unj g j n ( t ) ∈ U j n ，则 gnj(t) g j n ( t ) 可表示为

gnj(t)=∑ldj,nlu(2jt−l) g j n ( t ) = ∑ l d l j , n u ( 2 j t − l )

1、小波包分解算法

由 {dj+1,nl} { d l j + 1 , n } 求 {dj,2nl} { d l j , 2 n } 与 {dj,2n+1l} { d l j , 2 n + 1 } ：

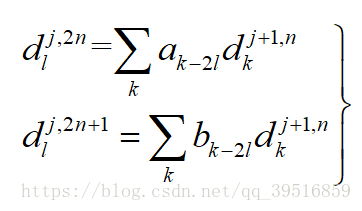
2、小波包重构算法

由 {dj,2nl} { d l j , 2 n } 求 {dj+1,nl} { d l j + 1 , n } 与 {dj,2n+1l} { d l j , 2 n + 1 } ：

dj+1,nl=∑k[hl−2kdj,2nk+gl−2kdj,2n+1k] d l j + 1 , n = ∑ k [ h l − 2 k d k j , 2 n + g l − 2 k d k j , 2 n + 1 ]

有关小波的几个术语及常见的小波基介绍见博客：https://blog.csdn.net/jbb0523/article/details/42586749