各种子序列:
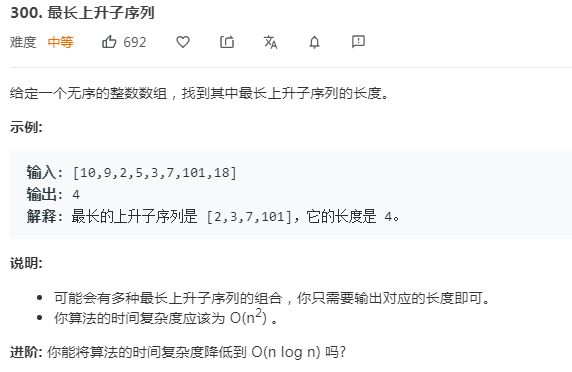
最长上升子序列(LIS):Longest Increasing Subsequence
最长连续序列(LCS):Longest Consecutive Sequence
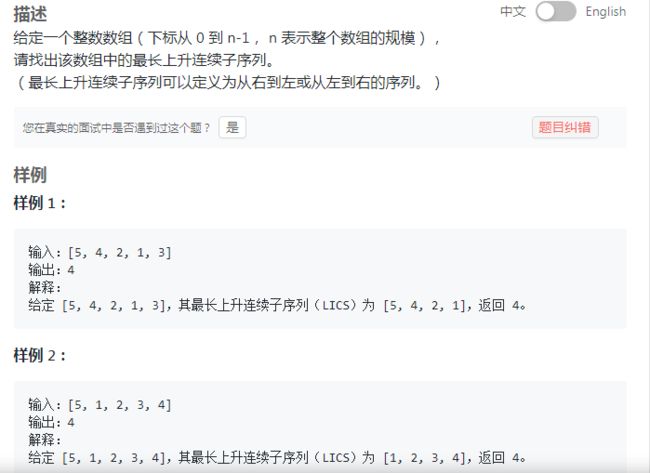
最长连续递增序列(LCIS):Longest Continuous Increasing Subsequence
最长公共子序列(LCS):Longest Common Subsequence
leetcode题库:
300 动态规划解最长子序列子串等一类问题之最长上升子序列[Thorold's Deer]
673/674动态规划解最长子序列子串等一类问题之最长连续递增序列[Reindeer]
1312动态规划解最长子序列子串等一类问题之让字符串成为回文及其Follow Up[Sika Deer]
128/LC397动态规划解最长子序列子串等一类问题之最长连续子序列[White-lipped Deer]
1143动态规划解最长子序列子串等一类问题之最长公共子序列[Hog Deer]
动态规划解最长子序列子串等一类问题之最长上升子序列[Thorold's Deer]
子串与子序列区别:子串不可跳跃,子序列可以跳跃,如 “AC”是“ABCDEFG”的子序列,而不是子串。 而“ABC”则是其子串
定义状态:
dp[i]dp[i]表示在区间nums[0....i]区间范围内的最长上升子序列的长度
比较索引ii与其前面出现的某个位置jj的大小
当nums[i]<=nums[j],说明jj处的值要比i处的值的,要是形成子序列则是nums[0...j,i]这样的结果,这时候j到i不能形成递增,以i结尾的子序列所形成的最长子序列的长度等价于以j结尾的子序列所形成的最长子序列的长度,即dp[i]=dp[j]
当nums[i]>nums[j],说明jj处的值小于i处值,形成的子序列是nums[0...j,i]这样的结果,这时候从j到i是递增的,这时候需要在长度上+1,即dp[i]=dp[j+1]
取上述两种情况的max,动态转移方程为: dp[i] = Math.max(dp[i], dp[j] + 1)|0<=j
举例:如果遍历到ii位置,在[0-i] 区间内有[0-j] j
边界条件:
当nums[0...i]只有一个元素时,即以这一个元素结尾的子序列,最长上升子序列是其自身,为1
核心代码
public int lengthOfLIS(int[] nums) {
//dp[i]: 到i为止 (对于所有 j in [0, i], 记录max length of increasing subsequence
if (nums == null || nums.length == 0) {
return 0;
}
int len = nums.length;
int[] dp = new int[len];
int res = 0;
for (int i = 0; i < len; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
//i 位置的数与[0,i]位置之间的数比较,如果大于进逻辑
if (nums[i] > nums[j]) {
//等于dp[i]或者dp[j] + 1(j对应的值比i小)的最大值
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
方法2:贪心+二分
准备一个辅助数组tails,其中tails[i]表示长度为i+1即nums[0...i]的序列尾部元素的值
辅助数组tails一定是严格单调递增的,即在nums[0...j..i]区间上,tails[j]
假设nums[0...j..i]这个区间上,tails[j]>=tails[i],从i这个子序列向前删除i-j个元素,这时候长度变为j的子序列,这时候的尾部元素的值为x
根据tails数组的定义,x
而x又是tails[j]的值,即x=tails[j]
得出tails[i]>tails[j],这与一开始假设的条件矛盾,假设条件不成立
public int lengthOfLISII(int[] nums) {
int n = nums.length;
int[] tails = new int[n];
int end = 0;
for (int i = 0; i < n; i++) {
int l = 0, r = end;
while (l < r) {
int m = (l + r) / 2;
if (tails[m] < nums[i]) l = m + 1;
else r = m;
}
tails[l] = nums[i];
if (end == r) end++;
}
return end;
}
动态规划解最长子序列子串等一类问题之最长连续递增序列[Reindeer]
题目要求最长连续递增序列,序列本身可以跳跃,但是题意要求连续,也即是不可跳跃
定义状态:
dp[i]表示以i位置结尾,即nums[i]值结尾的,最长连续递增序列的长度
只要关注当前位置i与其前一个的位置i-1的值的大小:
nums[i]>nums[i-1],i至少可以与i-1形成一个连续递增序列,因为它们俩挨着,并且是递增的,长度上是dp[i-1]+1
nums[i]<=nums[i-1],这时候,不能形成连续递增序列,后一个数要比前一个数小,呈下降的趋势,注意=不认为是递增的
方法1:DP(O(N))
public int findLengthOfLCIS(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);//至少可以与其自身形成递增序列
int max = 1;
for (int i = 1; i < n; i++) {
if (nums[i] > nums[i - 1]) {
dp[i] = dp[i - 1] + 1;
max = Math.max(max, dp[i]);
}
}
return max;
}
方法2:DP(O(1))
因为只会依赖于i与i-1这两个状态,借助一个常数的级别的一维数组dp[2],辅以奇偶数的小技巧
public int findLengthOfLCIS(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
int max = 1;
int[] dp = new int[2];
dp[0] = 1;
for (int i = 1; i < n; i++) {
dp[i % 2] = 1;//前一个状态值都会被覆盖,需要重新初始化
if (nums[i] > nums[i - 1]) {
dp[i % 2] += dp[(i - 1) % 2];//当前状态依赖前一状态,需要再前一状态上累加
}
max = Math.max(max, dp[i % 2]);
}
return max;
}
定义状态:
dp[i]表示以i位置结尾,即nums[i]值结尾的,最长连续递增序列的长度
dp初始化为1,因为nums[i]自身可以形成一个长度为1的最长递增序列
遍历[0...i],再套一层[0...j],其中j<i
当nums[j]<nums[i],说明以[...j,i]这段可以形成最长递增序列,长度是dp[j]+1,其中dp[j]是以j为结尾的最长递增序列的长度
当nums[j]≥nums[i],以[...j,i]是不能形成最长递增序列的,为dp[i],其被初始化为1了
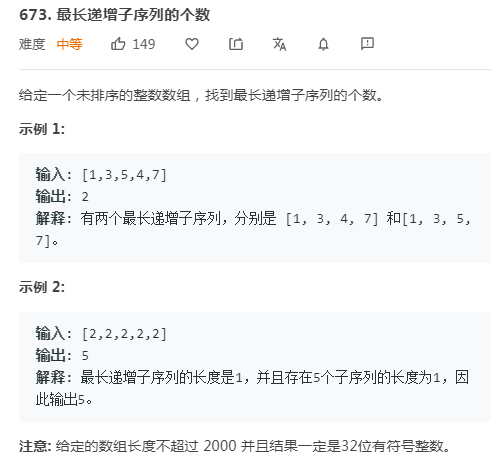
接下来要统计最长递增序列的个数,准备长度n的数组counter,定义count[i]为以nums[i]结尾的最长递增子序列的组合数量,这其中有两个限定条件,一是以nums[i]结尾,二是最长递增子序列,不是最长的不是这个counter数组考虑的,举例,1,2,4,3,5,4,7,2,最长递增序列有1,2,4,5,7;1,2,3,5,7;1,2,3,4,7三种情况,以nums[6]=7结尾的counter[6]=3
下面是如何生成这个counter数组:
总体要满足nums[i] > nums[j],才有意义,这样可以形成递增序列
当dp[j] + 1>dp[i],说明第一次找到以nums[i]为结尾的最长递增子序列,长度为dp[j] + 1,进而可以推出counter[i] = counter[j], 以nums[i]结尾的最长递增子序列的组合数=以nums[j]结尾的最长递增子序列的组合数,这个可以这么理解:当[...j]形成的组合数是值的话,其每一种组合结尾补上[i],即[...j,i],对于组合数本身是没有增加的,还是A值,唯独只是递增子序列的长度+1了
当dp[j] + 1=dp[i],说明这个长度已经找到过一次了,counter[i] += counter[j],现在的组合方式+counter[j]的组合方式
public int findNumberOfLIS(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
int[] dp = new int[n];
int[] counter = new int[n];
Arrays.fill(dp, 1);
Arrays.fill(counter, 1);
int max = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
if (dp[j] + 1 > dp[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
counter[i] = counter[j];
} else if (dp[j] + 1 == dp[i]) {
counter[i] += counter[j];
}
}
}
max = Math.max(max, dp[i]);
}
int res = 0;
for (int i = 0; i < n; i++) {
if (dp[i] == max) res += counter[i];
}
return res;
}
复杂度分析
时间复杂度:O(N^2),两个for loop
空间复杂度:O(N),dp与counter数组长度N
动态规划解最长子序列子串等一类问题之让字符串成为回文及其Follow Up[Sika Deer]
1.Step1
源问题,如上图,让字符串成为回文串的最少插入次数
定义状态
n为str的长度,dp[n][n]是一张二维表
定义:dp[i][j]表示的是子串str[i][j]最少添加多少字符可以使其整体变成一个回文,注意,是最少
要求的结果是dp[0][n-1]表示的是str[0...n-1]也就是这个字符从开头到结尾,要想形成回文,最少的添加字符的个数
如何填写这张dp table呢?
分三大类讨论
1. str[i...j]只有一个字符,即i==j,如图,str[i...j]=A,一个字符要形成回文,很简单,不要向其增加字符,即其本身可以形成回文,即dp[i][j]=0
2. str[i...j]有两个字符
2.1,当str[i]==str[j],即两个字符相同时,其与场景1的情况一样,例如,AA不需要添加字符,即可使其成为回文,即dp[i][j]=0
2.2,当str[i]!=str[j],即两个字符不同时,例如,AB,可以在前面加一个B,变成BAB,也可以在后面加一个A,变成ABA,总之是只要添加一个字符,即可使其变成回文,即dp[i][j]=1
3. str[i...j]有三个或者三个以上字符,这就属于一般的情况了
3.1.当str[i]==str[j]时,例如,ABDCA,只需要考虑BDC,也即要求dp[i][j],转化为求dp[i+1][j-1],只要搞定str[i+1...j-1]部分,使其变成回文,再加上str[i]与str[j],整体就变成回文了,即转移方程:dp[i][j]=dp[i+1][j-1]
3.2.当str[i]!=str[j]时,有两种方法使其变成回文,一种是先让str[i...j-1]变成回文,在ii的左边添加str[j],整体就会变成回文,例如ABECD,可以先考虑ABEC这部分,一个方案是ABECEBA,再在ABECEBA左边加上str[j],即D,带上源字符的D,变成了DABECEBAD;另外一种方案,同理,先让str[i+1...j]变成回文,最后在右边加上str[i],最终变成了整体回文,那么,动态转移方程式什么呢?
要想使str[i...j-1]变成回文,其最少的添加次数是dp[i][j-1],再加上往左侧补的字符,最终应该是dp[i][j-1]+1
同理可得,dp[i+1][j]+1
dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1
生成dptable的代码,注意遍历时,综合考虑了以上分析的三种情况
下文中需要使用到这个buildDP,做个一个抽离
public int minInsertions(String s) {
int[][] dp = buildDP(s.toCharArray());
return dp[0][s.length() - 1];
}
public int[][] buildDP(char[] chas) {
// $dp[i][j]$表示子串$str[i...j]$范围内的最少添加多少个字符后,可以形成回文子串
int n = chas.length;
int[][] dp = new int[n][n];
for (int j = 1; j < n; j++) {
dp[j - 1][j] = (chas[j - 1] == chas[j]) ? 0 : 1;
for (int i = j - 2; i >= 0; i--) {
if (chas[i] == chas[j]) dp[i][j] = dp[i + 1][j - 1];
else dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]) + 1;
}
}
return dp;
}
复杂度分析
时间复杂度:O(N^2),N是字符的长度
空间复杂度:O(N^2),dp表的空间
2.Step2
给定一个字符串str,如果可以在str的任意位置添加字符,请返回在添加字符最少的情况下,让str整体都是回文字符串的结果。
这个问题比Step1的问题多了一步,要求返回一种使其变成整体回文的结果,例如,源字符AB,返回一种添加最少字符,使其变成回文的一种方案,返回ABA或者BAB均可
解题思路
准备一个res数组,长度是字符s本身的长度+dp[0][n-1]
运用双指针的想法,给res填充字符
当str[i]==str[j]时,res直接追加即可
当str[i]!=str[j]时,需要找到一个最少添加字符的方案
当dp[i][j - 1] < dp[i + 1][j]时,即最终在生成字符的时候,在左侧填充一个str[j]
当dp[i][j - 1] >= dp[i + 1][j]时,即最终在生成字符的时候,在右侧填充一个str[i]
public String getPalindromeI(String s) {
char[] chas = s.toCharArray();
int n = chas.length;
int[][] dp = buildDP(chas);
int appendLen = dp[0][n - 1];
char[] res = new char[n + appendLen];
int i = 0, j = n - 1;
int left = 0, right = res.length - 1;
while (i <= j) {
if (chas[i] == chas[j]) {
res[left++] = chas[i++];
res[right--] = chas[j--];
} else {
if (dp[i][j - 1] < dp[i + 1][j]) {
res[left++] = chas[j];
res[right--] = chas[j--];
} else if (dp[i][j - 1] >= dp[i + 1][j]) {
res[left++] = chas[i];
res[right--] = chas[i++];
}
}
}
return String.valueOf(res);
}
复杂度分析
时间复杂度:O(N^2),N是字符的长度,求res的过程是O(N),总体是O(N^2)
空间复杂度:O(N^2),dp表的空间
3.Step3
给定一个字符串str,再给定str的最长回文子序列字符串strlps,请返回在添加字符最少的情况下,让str整体都是回文字符串的一种结果。进阶问题比原问题多了一个参数,请做到时间复杂度比原问题的实现低
举例:
str="A1B21C",strlps="121",返回"AC1B2B1CA"或者"CA1B2B1AC",总之,只要是添加的字符数最少,只返回其中一种结果即可
题目分析
这个问题是给出了一个seed字符,生成最少添加字符形成回文后的其中一种结果
解题思路
运用剥洋葱的方式去解决
str的长度为nn,strlps的长度为m,形成回文res的结果是2*n-m ,因为m部分已经是回文了,不需要额外添加
以str=A1BC22DE1F,strlps=1221为例
洋葱的第0层是由strlps[0]与strlps[m-1],组成,即1...1,从str的最左侧开始找,一直找到strlps[0]=1的字符为止,记为leftPart,为A,接着从str的最右侧开始找,一直找到strlps[m-1]=1的字符为止,记为rightPart,为F,
将leftPart+rightPart的逆序leftPart+rightPart的逆序,复制到res的左侧
将rightPart+leftPart的逆序rightPart+leftPart的逆序,复制到res的右侧
结果变成了AF......FA
在加上strlps,变成了AF1......1FA
洋葱进入第1层,即2...2,接着第一层的位置找str,leftPart为BC,rightPart为DE,
将leftPart+rightPart的逆序leftPart+rightPart的逆序,复制到res的左侧
将rightPart+leftPart的逆序rightPart+leftPart的逆序,复制到res的右侧
结果变成了BCED......DECB
在加上strlpsstrlps,变成了BCED2......2DECB
加上上一层,变成了AF1BCED22DECB1FA
洋葱进入第n层。。。
代码部分注释掉了一部分,将resLeft = 0, resRight = 0;定义为全局变量,好理解些
整体实现逻辑是双指针,游走,不过左右指针有很多对,嗯,只能是,细节是魔鬼啊
//res array 的左右指针,定义为全局变量
int resLeft = 0, resRight = 0;
public String getPalindromeII(String str, String strlps) {
char[] chas = str.toCharArray();//str 目标字符串
char[] lps = strlps.toCharArray();//base 字符串
int n = chas.length, m = lps.length;//len
char[] res = new char[2 * n - m];//res字符串 arr
int chasLeft = 0, chasRight = n - 1;//str 的左右指针
int lpsLeft = 0, lpsRight = m - 1;//base 的左右指针
resRight = res.length - 1;
int tmpLeft = 0, tmpRight = 0;//tmp 左右指针
while (lpsLeft <= lpsRight) {//循环遍历lps字符
tmpLeft = chasLeft;
tmpRight = chasRight;
while (chas[chasLeft] != lps[lpsLeft]) chasLeft++;//如果lpsLeft在chas未出现,一直chasLeft++
while (chas[chasRight] != lps[lpsRight]) chasRight--;//如果lpsRight在chas未出现,一直chasRight--
build(res, chas, chasLeft, chasRight, tmpLeft, tmpRight);//组装
// int len = chasLeft - tmpLeft + tmpRight - chasRight;
// resLeft += len;
// resRight -= len;
res[resLeft++] = chas[chasLeft++];//添加当前的lpsLeft ==lpsRight对于的字符串
res[resRight--] = chas[chasRight--];//添加当前的lpsLeft ==lpsRight对于的字符串
lpsLeft++;//进入下一轮
lpsRight--;
}
return String.valueOf(res);
}
/**
* @param res 结果arr
* // * @param resLeft
* // * @param resRight
* @param chas str arr
* @param chasLeft str arr left pointer
* @param chasRight str arr right pointer
* @param tmpLeft tmp left pointer
* @param tmpRight tmp right pointer
*/
private void build(char[] res,
char[] chas, int chasLeft, int chasRight,
int tmpLeft, int tmpRight) {
for (int i = tmpLeft; i < chasLeft; i++) {
res[resLeft++] = chas[i];
res[resRight--] = chas[i];
}
for (int j = tmpRight; j > chasRight; j--) {
res[resLeft++] = chas[j];
res[resRight--] = chas[j];
}
}
动态规划解最长子序列子串等一类问题之最长连续子序列[White-lipped Deer]
方法1:Sort+Compare
先排序,题意要求连续序列,即可以比较nums[i]与 nums[i - 1],如果不相等,表示是递增的趋势,相等则反之,递增后需要判断是否连续,即相邻的元素差值是否为1
下面的代码处理边界case 如[-1,0],不会比较max与cur的值,需要在最后一道防线拦截一次
Math.max(max,cur);
public int longestConsecutive(int[] nums) {
if (nums == null || nums.length == 0) return 0;
Arrays.sort(nums);
int n = nums.length;
int max = 1, cur = 1;
for (int i = 1; i < n; i++) {
if (nums[i] != nums[i - 1]) {
if (nums[i - 1] + 1 == nums[i]) cur++;
else {
max = Math.max(max, cur);
cur = 1;
}
}
}
return Math.max(max, cur);
}
复杂度分析
时间复杂度:O(Nlog(N)),N是数组的长度,排序的复杂度
空间复杂度:O(1),常量级别的空间
方法2:Hash
准备一个set,首先将所有的num装进set
for loop 数组,如果当前遍历到的元素num-1不在set中,说明这是一段新的可能出现的递增序列,变量curNum置为num,while循环判断curNum+1是否在set中,是则表示是连续的
记录max值
public int longestConsecutive(int[] nums) {
Set set = new HashSet<>();
for (int num : nums) set.add(num);
int max = 0;
for (int num : nums) {
if (!set.contains(num - 1)) {//判断set不包含当前元素-1的值,跳过已经计算的最长递增序列
int curNum = num;
int curCnt = 1;
while (set.contains(curNum + 1)) {
curNum += 1;
curCnt += 1;
}
max = Math.max(max,curCnt);
}
}
return max;
}
复杂度分析
时间复杂度:O(N),尽管在 for 循环中嵌套了一个 while循环,时间复杂度看起来像是二次方级别的。但其实它是线性的算法。因为只有当 curNum 遇到了一个序列的开始,$ while 循环才会被执行(也就是$ curNum-1 不在数组 nums 里), while循环在整个运行过程中只会被迭代N次。这意味着尽管看起来时间复杂度为 O(N^2), 实际这个嵌套循环只会运行 O(N+N)=O(N)次。所有的计算都是线性时间的,所以总的时间复杂度是O(N)的
空间复杂度:O(1),常量级别的空间
最长上升连续子序列
使用 O(n) 时间和 O(1) 额外空间来解决
O(1)的空间复杂度来处理,会比较麻烦,需要压缩空间,题意中的最长上升连续子序列,定义为从左到右和从右到左均可以
准备两个数组,大小都为2:
start记录从左到右的连续递增子序列的最长长度
end记录从右到做的连续递增子序列的最长长度
public int longestIncreasingContinuousSubsequence(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
//从左到右,start
int[] start = new int[2];
Arrays.fill(start, 1);
int maxStart = 1;
for (int i = 1; i < n; i++) {
start[i % 2] = 1;
if (nums[i] > nums[i - 1]) {
start[i % 2] += start[(i - 1) % 2];
}
maxStart = Math.max(maxStart, start[i % 2]);
}
//从右到做,end
int[] end = new int[2];
Arrays.fill(end, 1);
int maxEnd = 1;
for (int i = n - 2; i >= 0; i--) {
end[i % 2] = 1;
if (nums[i] > nums[i + 1]) {
end[i % 2] += end[(i + 1) % 2];
}
maxEnd = Math.max(maxEnd, end[i % 2]);
}
return Math.max(maxStart, maxEnd);
}
动态规划解最长子序列子串等一类问题之最长公共子序列[Hog Deer]
方法1:DP 基础版
对于0位置未添加空字符串
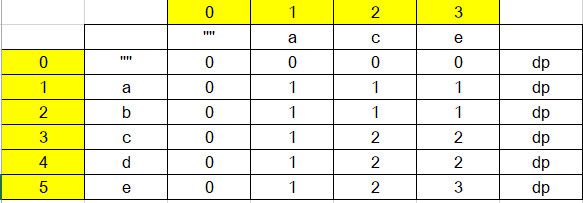
dp[i][j]表示的是s1[0...i-1]与s2[0...j-1]的最长公共子序列的长度,要求的是dp[m-1][n-1]
当s1[i]==s2[j],说明这两个字符是公共的字符,只要考察其子问题,dp[i-1][j-1]的长度即可,在此基础上+1,
当s1[i]!=s2[j],说明这两个字符不是公共的字符,只要考察其两个子问题,dp[i-1][j],dp[i][j-1],取max
动态转移方程:
public int longestCommonSubsequence(String text1, String text2) {
if (text1 == null || text2 == null || text1.length() == 0 || text2.length() == 0) return 0;
char[] chas1 = text1.toCharArray();
char[] chas2 = text2.toCharArray();
int m = chas1.length, n = chas2.length;
int[][] dp = new int[m][n];
dp[0][0] = chas1[0] == chas2[0] ? 1 : 0;
for (int i = 1; i < m; i++) dp[i][0] = chas1[i] == chas2[0] ? 1 : dp[i - 1][0];
for (int j = 1; j < n; j++) dp[0][j] = chas1[0] == chas2[j] ? 1 : dp[0][j - 1];
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
if (chas1[i] == chas2[j]) dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
}
}
return dp[m - 1][n - 1];
}
方法2:DP 优化版
对于0位置添加空字符串
dp[i][j]表示的是s1[0...i]与s2[0...j]的最长公共子序列的长度,要求的是dp[m][n]
注意s1|s2的位置是错位了一个,其长度达不到m|n
public int longestCommonSubsequence2nd(String text1, String text2) {
if (text1 == null || text2 == null || text1.length() == 0 || text2.length() == 0) return 0;
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
return dp[m][n];
}
方法3:DP压缩空间版O(1)
准备一个dp,n+1的长度,其实的0位置存放一个空字符串
准备几个变量:
last:表示是当前dp[j](dp[i][j])左上角的数,相当于dp[i-1][j-1],初始化的时候为0
tmp:表示是当前dp[j](dp[i][j])正上方的数,相当于dp[i- 1][j]
dp[j-1]:表示是当前dp[j](dp[i][j])左边的数,相当于dp[i][j-1]
每一轮结束后,last的值都向前滚动一个,变成正上方的数,也就是tmp
public int longestCommonSubsequence3rd(String text1, String text2) {
if (text1 == null || text2 == null ||
text1.length() == 0 || text2.length() == 0) return 0;
int m = text1.length(), n = text2.length();
int[] dp = new int[n + 1];
int tmp = 0;
for (int i = 1; i <= m; i++) {
int last = 0;
for (int j = 1; j <= n; j++) {
tmp = dp[j];
if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[j] = last + 1;
else dp[j] = Math.max(tmp, dp[j - 1]);
last = tmp;
}
// System.out.println(JSON.toJSONString(dp));
}
return dp[n];
}
参考链接:
https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/dong-tai-gui-hua-jie-zui-chang-zi-xu-lie-zi-chua-3/
https://leetcode-cn.com/problems/number-of-longest-increasing-subsequence/solution/dong-tai-gui-hua-jie-zui-chang-zi-xu-lie-zi-chua-4/
https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/solution/dong-tai-gui-hua-jie-zui-chang-zi-xu-lie-zi-chuan-/
https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/solution/dong-tai-gui-hua-jie-zui-chang-zi-xu-lie-zi-chuan-/
https://leetcode-cn.com/problems/longest-consecutive-sequence/solution/dong-tai-gui-hua-jie-zui-chang-zi-xu-lie-zi-chua-5/
https://leetcode-cn.com/problems/longest-common-subsequence/solution/a-fei-xue-suan-fa-zhi-by-a-fei-8/