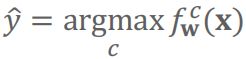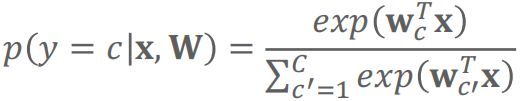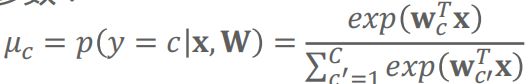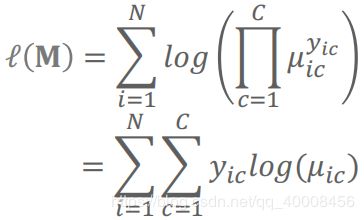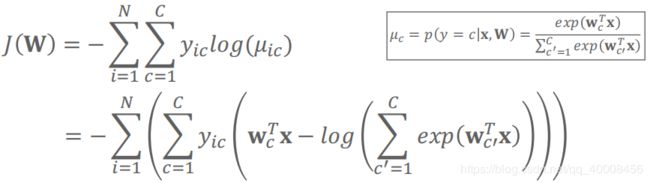Logistic回归,多类分类
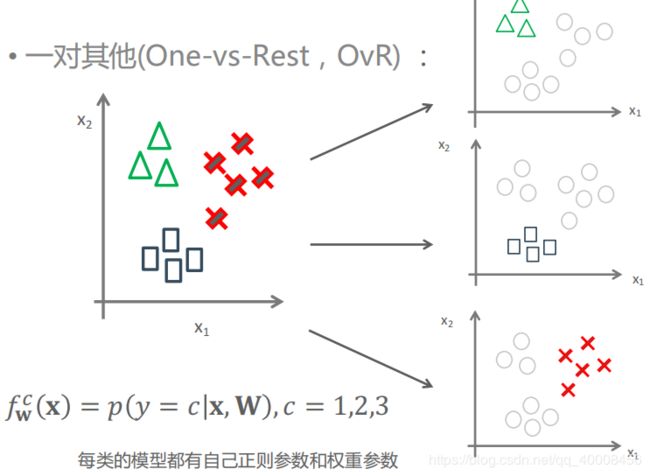
1对其他(One-vs-Rest,OvR):
对每个类别c,训练一个Logistic回归分类器![]() ,预测y=c概率
,预测y=c概率
对新的输入x,选择使得![]() 最大的类别作为预测(最大后验估计,MAP):
最大的类别作为预测(最大后验估计,MAP):
多项分布
在概率分布中,贝努利(Bernoulli)分布的输出只有两种取值。
Multinoulli分布,或称为范畴分布(categorical distribution),输出有K种取值。
类似用Bernoulli分布描述两类分类的概率分布,可用Multinoulli分布描述多类分类的概率分布,其参数为向量![]() ,其中
,其中![]() ,其中每一个分量
,其中每一个分量![]() 表示第c个状态的概率。用符号Cat(y;θ)表示。
表示第c个状态的概率。用符号Cat(y;θ)表示。
将类别y用独热编码(编码为C维向量,当y=c时,第c维为1,其他元素均为0),记为向量y
则Multinoulli分布的概率函数为:![]() ,其中
,其中![]() 表示向量y的第c个元素
表示向量y的第c个元素
或者用标量形式记为:![]() ,其中I(.)为示性函数,当括号中条件满足时函数值为1,否则为0。
,其中I(.)为示性函数,当括号中条件满足时函数值为1,否则为0。
Softmax分类器
类似两类分类模型推导,假设输出y=c的概率可以由x的线性组合再经过sigmoid函数变换得到
则模型为:
上述等式右边为Softmax函数。Softmax函数为sigmoid函数的推广,将C维向量的每个元素转换为[0,1]的数,且变换后元素之和为1: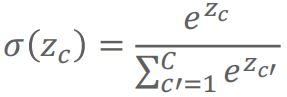
因此得到的分类器被称为Softmax分类器。
向量μ表示Multinoulli分布的参数:
令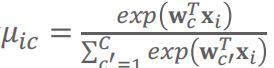 ,
,![]() 为第i个样本的类别,则Softmax分类模型的log似然函数为:
为第i个样本的类别,则Softmax分类模型的log似然函数为:
则极大似然估计等价于最小训练集上的Softmax损失/负log似然损失:
正则项:Softmax分类模型的正则项同两类分类模型
目标函数优化方法:同两类分类模型
Logistic回归优化求解
Scikit-Learn中实现Logistic回归的类
class sklearn.linear_model.LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’liblinear’, max_iter=100, multi_class=’ovr’, verbose=0, warm_start=False, n_jobs=1)
参数multi_class决定了多类分类的实现方式,可选:
1、‘ovr’:即1对其他(one-vs-rest,OvR),将多类分类转化为多个二类分类任务。为了完成第C类的分类决策,将所有第C类的样本作为正例,除了第c类样本以外的所有样本都作为负例,每个类别的二分类器单独训练。
2、‘multinomial’:Softmax回归分类,对多项分布概率整体进行训练。
注意:multi_class选择会影响优化算法solver参数的选择
OvR:可用所有的slover
Multinomial:只能选择newton-cg,lbfgs和sag/saga(liblinear不支持)