最长路径矩阵(LPM)计算迭代边界
LPM算法计算迭代边界,具体参考陈弘毅等人译的《VLSI数字信号处理系统设计与实现》2.4.1
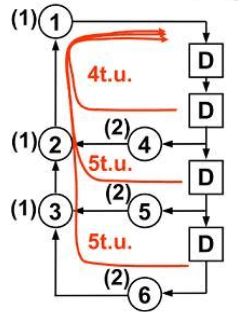
d d d 表示DFG中延时的数目。矩阵 L ( 1 ) \bf{L}^{(1)} L(1) 中:从延时单元 d i d_i di 到延时单元 d j d_j dj 中正好经过0个延时(不包含 d i d_i di 和 d j d_j dj)的所有路径中, l i , j 1 l_{i,j}^1 li,j1 表示最长的运算时间。如果这样的路径不存在,那么 l i , j 1 = − 1 l_{i,j}^1=-1 li,j1=−1。对于如图所示的数据流图(DFG)
L ( 1 ) = [ − 1 0 − 1 − 1 4 − 1 0 − 1 5 − 1 − 1 0 5 − 1 − 1 − 1 ] \bf{L}^{(1)} = \begin{bmatrix} -1 & 0 & -1 & -1\\ 4 & -1 & 0 & -1\\ 5 & -1 & -1 & 0\\ 5 & -1 & -1 & -1 \end{bmatrix} L(1)=⎣⎢⎢⎡−14550−1−1−1−10−1−1−1−10−1⎦⎥⎥⎤
采用如下程序即可计算得到DFG的迭代边界 T b o u n d T_{bound} Tbound。
# -*- coding: UTF-8 -*-
# 最长路径矩阵:LPM
import numpy as np
d = 4
L1 = np.array([[-1, 0, -1, -1], [4, -1, 0, -1], [5, -1, -1, 0], [5, -1, -1, -1]])
L = -np.ones([d, d, d]) # 这里是考虑到K可能是空集
L[0, :, :] = L1
for m in range(1, d):
for j in range(0, d):
for i in range(0, d):
H = np.ones(d)
for k in range(0, d):
if L[0, i, k] == -1 or L[m-1, k, j] == -1:
H[k] = 0
M = -np.ones(d)
for k in range(0, d):
if H[k] != 0:
M[k] = L[0, i, k] + L[m-1, k, j] # 这里是考虑到K可能包含不只一个取值
Max = np.max(M)
L[m, i, j] = np.maximum(-1, Max)
k = 0
T = np.ones(d*d)
for m in range(1, d+1):
for i in range(0, d):
T[k] = L[m-1, i, i]/m
k = k + 1
T_bound = np.max(T)
欢迎在评论区指正。