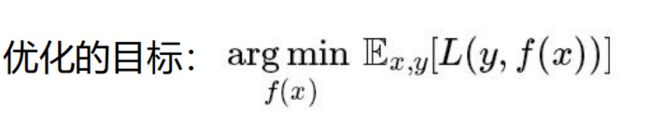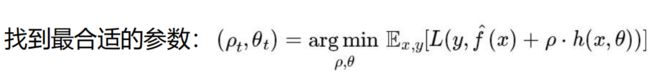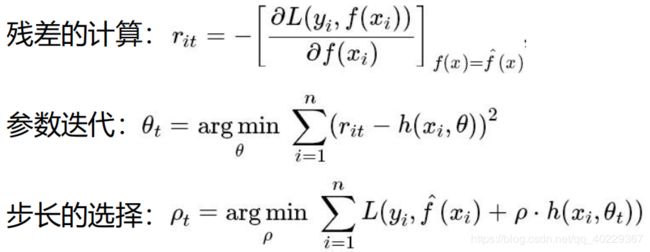GBDT算法

GBDT算法 Gradient Boosting Decision Tree

以梯度为优化目标，以提升为手段（前面讲到的集成算法中的串联），基础模型为决策树（这里用的是回归树）的算法

GBDT简单来说，就是用多个树串联，提升模型的效果

 

以下是学习唐宇迪老师的GBDT算法的理解，文末有其他直接更详细的的关于GBDT算法的实现

回归树的形式是CART 即二叉树

使用回归树做分类和回归都可以

我们希望分类的话是残差尽量小，使损失函数小，而回归，数据离均值近

衡量回归树分类效果我们用的是利用变换到exp函数上属于哪一类的概率从而得到损失函数的值

衡量回归树回归效果我们用的是最小二乘法，实际值和均值之差的平方累和

 

GBDT核心为GB算法，它的优化目标是使损失函数最小

f(x)即为我们建立的模型，L函数是损失函数，意思是什么样的模型能够使得到损失函数最小（数据得到合理分配）

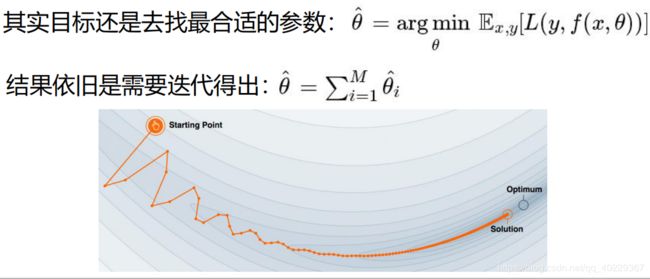
那么对于GBDT算法来说，就是找到合理的参数（模型的参数和各模型的合理的分配比例，因为这里用到的是多棵树）

因此这里的迭代也就是我们需要进行的以梯度方式逼近最优解

那么衡量是不是合适的参数，就需要用到损失函数，损失函数有很多种

这里的y是实际值，F(x)是我们的预测值

选择不同的损失函数，其值也会不一样

我们得到我们的目标函数：

这里的参数p是各树其分配比例，也可以当做是该树的学习率、步长，sita是回归树的参数

我们进行拟合回归树的依据就是残差，残差使用的是损失函数的一阶导，这里我们称之为负梯度（求的是残差最小值）

参数迭代和步长选择就是对GB算法的参数选择，也就是希望GBDT算法的效果比较好，这两个参数都需要比较合理

 

GBDT工作过程如下（分类回归都是，只不过处理方式有些区别）

下面我们直接分别以回归任务和分类任务来说明它的工作过程，了解完例子以后再回来看这个数据表达的工作过程就好懂很多

回归任务：

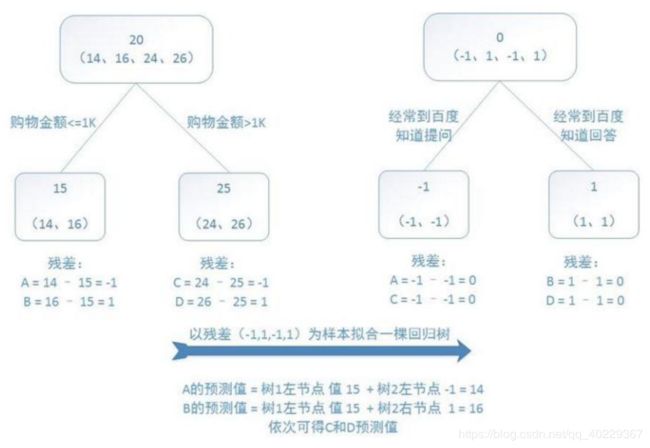
回归任务结果我们需要的是数值

一开始对第一棵树使用的的是实际值，也就是原始的数据，之后产生对应残差作为输出，

之后的树，使用的都是前面的树产生的残差作为输入

像上面的，计算残差的方式比较简单就是和平均值相减，

在实际训练过程中，一开始我们允许可以生成比较多的树，但之后只要发现残差不怎么变了，就可以停止训练了（认为此时损失值是最小了的）

（大多数使用多棵树小学习率来进行，类似梯度的情况，避免越过了最优解）

而怎么得到预测值呢：得到实际数据作为第一棵树的输入，然后得到对应叶子节点的的均值然后按特征去到相应的分支得到对应的残差

预测值=均值+残差

 

分类任务：

分类任务和逻辑回归有点像，得到的分类是某一类的概率值，也就是有多大的概率是这类

下面以一个三分类问题作为例子

对于三分类问题，就是建立三棵树，每一棵树表示：是不是属于该类，

比如第一棵树——是否属于第一类

第一棵树是100 第二棵树是010 第三棵树是001 （有点像OneHot Encoding）

假设以某一条件作为分类（切分节点），看是不是可能属于第二类那么就用上面的第一条式子计算，如果数据真的是比较像第二类，那么f11接近0，f22接近1,f33接近0，就是比较接近第二类，f22大，第二类可能性较大，

那么第一步就是用实际值计算残差，后面的树的输入都是前面一棵树计算的残差

总体下来，按照某一分类作为节点得到的残差越小越好，也就是损失值越小

训练的时候就是找到一个能使残差越小的分类条件作为节点构成的树

预测的时候就是“跑树”，看他更像哪一棵树

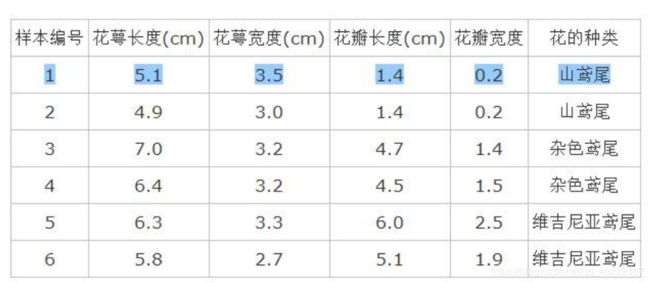
以这个为例，假设第一棵树就用到了花萼长度作为标准，以这个特征的某一特征值，如5.1，作为分支条件，<5.1的是1，>=5.1的不是1，那么6个样本中就只有2号是分到1，其余的在不是1 的分支中，计算残差时我们更关注计算的是那些分不好类的数据，先计算他们是不是属于该类的概率p，因此前者为 1（2号标签为1） -1=0，里面的数据的确都是1，而后者为 1（总和为1 ，只有一个标签为1的：1-0=1,而有4个0-0）/5=0.2，也就是5个数据当中有一个是1

因此计算残差（计算残差的方式各有不同）

对于1号：(1-0.2)^2（对于1来说残差大，说明这样分不合理）

其余的（除了2号，他是分对了(1-1）^2=0): (0-0.2)^2 （其他不为1的，其残差比较小，说明的确不是1这类的）

前面1 和0 是说他们标签是不是第一类

之后就是把残差累和，就是现在以这个标准分类的模型的残差

那么优化残差也就是优化了模型，把应该分在一起的放在一起，不是的就下一棵树

（说明：大家会发现计算残差的方式不同，其实选用不同的损失函数计算残差的方式也不一样，这里选的是简单方便理解的一种形式）

流程总结：
1.初始化残差，构成弱学习器1。（预测特征所对应得特征值求平均值）
2.计算残差（实际值 - 弱学习器1）。
3.寻找回归树的最佳划分点（阈值）。遍历每个特征的每个特征值作为阈值，通过阈值将数据二分，分别计算方差，找到使方差最小的特征值为最佳二分阈值
4.将二分后的残差值更新为实际值，计算实际值平均值 作为残差。构成弱学习器2。
5.合并强学习器。（弱学习器1 + 弱学习器2）
6.满足条件迭代停止
 

下面附上可视化网址：

http://arogozhnikov.github.io/2016/06/24/gradient_boosting_explained.html

http://arogozhnikov.github.io/2016/07/05/gradient_boosting_playground.html

 

参考学习文章：

更详细的用GBDT回归任务的解释：

https://blog.csdn.net/qq_22238533/article/details/79185969

更详细的用GBDT分类任务的解释：

https://blog.csdn.net/qq_22238533/article/details/79192579