第十一届蓝桥杯大赛第二次模拟（软件类C/C++）个人总结

题目链接

官网 辅导资料 2020年4月 本科组

视频传送门

填空题

1. 12.5MB

【解题思路】

bit是位，B是字节，1B = 8bit，除此之外任意两个都是1024的距离。

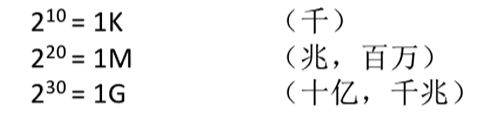
所以手机的4GB内存就是$4\ast 2^{30}=2^{32}$个字节（B）

【代码】

//在计算机存储中，12.5MB是多少字节？
#include
using namespace std;
int main(){
	int res = 12.5*1024*1024;
	printf("%d", res);
	return 0;
}

【结果】

13107200

2. 最多边数

【解题思路】

n个结点的有向边，那么每个结点都可以连接另外n-1个结点，总共n个结点，那么总边数是$n\ast (n-1)$

【代码】

//一个包含有2019个结点的有向图，最多包含多少条边？（不允许有重边）
#include
using namespace std;
int main(){
	int n = 2019;
	printf("%d", n*(n-1));
	return 0;
}

【结果】

4074342

3. 单词重排

【解题思路】

STL的好处体现出来了。枚举所有排列的另一个方法是从字典序最小排列开始，不停调用“求下一个排列”的过程。如何求下一个排列呢？C++的STL中提供了一个库函数next_permutation。把所有排列都送到set集合中去重，最后输出set的大小就行了。

比手算可快多了。

【代码】

/*
将LANQIAO中的字母重新排列，可以得到不同的单词。 
如LANQIAO、AAILNOQ等，注意这7个字母都要被用上，单词不一定有具体的英文意义。
请问，总共能排列如多少个不同的单词。
*/ 

#include
#include
#include
using namespace std;
set<string> words;
string letters = "LANQIAO";
int main(){
	sort(letters.begin(), letters.end());
	do{
		words.insert(letters);
//		cout<
	}while(next_permutation(letters.begin(), letters.end()));
	cout<<words.size(); 
	return 0;
}

【结果】

2520

4. 括号序列

【解题思路】

这个n = 4，看着挺小的自己在草稿纸上枚举都行。但是遇到这种题要想着怎么用代码解决，因为往往真到考试的时候就是靠手写解决不了的规模。

用递归的思想写一个DFS，参数应该包括当前处理的位置idx，比如4对括号要填8处，已经使用的左括号的个数ln，已经使用的右括号数rn。

下一个状态的判断：

• 只要表达式中左括号的个数大于等于右括号的个数，并且已经用的左括号没超过可用的，就可以在idx处放左括号 ；
• 只要表达式中右括号的个数小于左括号的个数，并且已经用的右括号没超过可用的，就可以在idx处放右括号；

递归边界的判断：

• 处理到了第$2\ast n$位，从第0位开始填，0~$2\ast n-1$刚好是$2\ast n$个符号。

【代码】

/*
由1对括号，可以组成一种合法括号序列：()。
由2对括号，可以组成两种合法括号序列：()()、(())。
由4对括号组成的合法括号序列一共有多少种？
*/ 

#include
using namespace std;
int n = 4; // n表示左括号和右括号的个数 
int cnt = 0; //结果 
void dfs(int idx, int ln, int rn){
	// idx表示当前处理第几位，ln、rn分别表示已经用了的左右括号个数 
	if(idx == 2*n){
		cnt++;
		return;
	}
	if( (ln >= rn) && (ln < n)){
		//只要表达式中左括号的个数大于等于右括号的个数，并且已经用的左括号没超过可用的，就可以在idx处放左括号 
		dfs(idx+1, ln+1, rn); 
	}
	if( (rn < ln) && (rn < n)){
		//只要表达式中右括号的个数小于左括号的个数，并且已经用的右括号没超过可用的，就可以在idx处放右括号 
		dfs(idx+1, ln, rn+1);
	}
}
int main(){
	dfs(0, 0, 0); 
	printf("cnt:%d", cnt);
	return 0;
}

【结果】

cnt:14

编程题

5. 反倍数

【解题思路】

放心枚举。

【代码】

/*
给定三个整数 a, b, c：
如果一个整数既不是 a 的整数倍也不是 b 的整数倍还不是 c 的整数倍。 
则这个数称为反倍数，请问在 1 至 n 中有多少个反倍数。
*/ 
#include
using namespace std;
int main(){
	int n;
	scanf("%d", &n);
	int a, b, c;
	scanf("%d%d%d", &a, &b, &c);
	int ans = 0;
	for(int i=1; i<=n; i++){
		if(i%a==0 || i%b==0 || i%c==0){
			continue;
		}
		else{
			ans++;
		}
	}
	printf("%d", ans);
	return 0;
}

6. 凯撒加密

【解题思路】

这种在一定范围内循环的感觉就要善用%。

【代码】

/*
给定一个单词，请使用凯撒密码将这个单词加密。
凯撒密码是一种替换加密的技术，单词中的所有字母都在字母表上向后偏移3位后被替换成密文。
即a变为d，b变为e，...，w变为z，x变为a，y变为b，z变为c。
例如，lanqiao会变成odqtldr。
*/ 
#include
#include 
using namespace std;
int main(){
	string str;
	cin>>str;
	for(int i=0; i<str.length(); i++){
		char ch = (str[i]-'a'+3) % 26 + 'a';
		cout<<ch;
	}
	return 0;
}

7. 螺旋

【解题思路】

螺旋填数，这类题经常遇到。首先我们要确定并维持一个方向，就是当前填数的方向，然后朝这个方向填到底了，就转90°继续填。

本题中可以用四个整数0, 1, 2, 3分别表示右下左上，初始方向d = 0，然后d方向填到底，就顺时针变换d++，因为一直这么顺时针的转，刚好是$（d+1）$%$4$。
朝着当前方向d走一步，经常用增量矩阵：

int direction[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 右下左上

为了旋转中判断哪些框填过数了，用一个bool型的数组checked表示当前位置的框子是否有数了，那么思路就清楚了，直接看代码：

【代码】

/*
对于一个 n 行 m 列的表格，我们可以使用螺旋的方式给表格依次填上正整数，我们称填好的表格为一个螺旋矩阵。
例如，一个 4 行 5 列的螺旋矩阵如下：
1 2 3 4 5
14 15 16 17 6
13 20 19 18 7
12 11 10 9 8
*/
#include
using namespace std;
const int maxn = 1010;
int num[maxn][maxn];
bool check[maxn][maxn] = {false};
int direction[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 右下左上 
int main(){
	int n, m;
	scanf("%d%d",&n, &m);
	int pos_x, pos_y;
	scanf("%d%d", &pos_x, &pos_y); 
	int x=1, y=1, times = 0;
	// 0, 1, 2, 3分别表示右下左上
	int d = 0; 
	int number = 1;
	while(times < n*m){
		if(!check[x][y]){
			num[x][y] = number;
			number++;
			check[x][y] = true;
			times++;
		}
		// 如果朝着d方向走一步不可行，就顺时针改变方向。 
		if(x+direction[d][0] == n+1 || y+direction[d][1] == m+1 || x+direction[d][0] == 0 || y+direction[d][1] == 0){
			d = (d+1)%4;
		} 
		else if(check[x+direction[d][0]][y+direction[d][1]]){
			d = (d+1)%4;
		}
		if(x == pos_x && y == pos_y){
			break;
		} 
		// 更新位置 
		x += direction[d][0];
		y += direction[d][1];
	}
	printf("%d", num[pos_x][pos_y]);
	return 0;
}

8. 摆动序列

这道题和第一次模拟的第九题序列计数特别特别像，我学会了！

【解题思路】

方法一：按照题意进行记忆性递归。当然过不了所有的样例，但是思想简单直接，容易想到这里拿到一定分数。

用$f(cur,pos)$表示第pos位上的数为cur的摆动序列个数，pos从1开始，那么$n=4$可以得到下面的递归图（没有写完）：

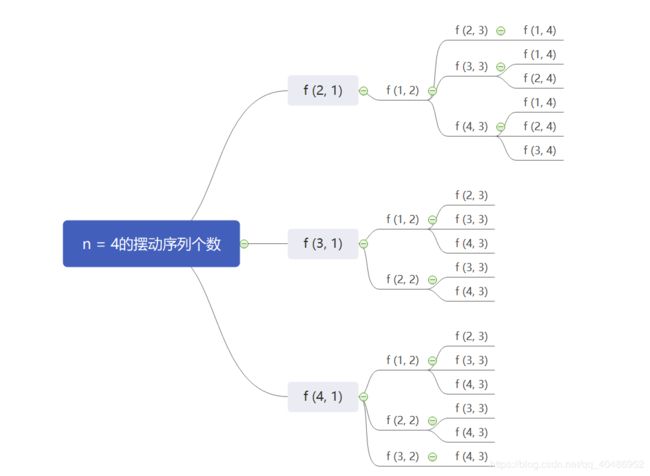
可以看到有很多相同的状态，这也是为什么要用记忆型递归的原因。

所以$n=4$的摆动序列个数应该等于$f(2,1)+f(3,1)+f(4,1)$，而这每个子表达式的结果又和pos有关（摆动序列），那么很容易写出递归：

• 递归边界：$pos==m$，填完了m位就结束了。

• 递推式：

  1. 如果$cur$在奇数列，即pos % 2 == 1：$f(cur,pos)=f(1,pos+1)+f(2,pos+1)+...+f(cur-1,pos+1)$
  2. 如果$cur$在偶数列，即pos % 2 == 0：$f(cur,pos)=f(cur+1,pos+1)+f(cur+2,pos+1)+...+f(n,pos+1)$

【代码】

/*
如果一个序列的奇数项都比前一项大，偶数项都比前一项小，则称为一个摆动序列。即 a[2i]a[2i]。
小明想知道，长度为 m，每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
*/
#include
using namespace std;
const int maxn = 1010;
const int MOD = 10000;
int mem[maxn][maxn];
int m, n;
long long f(int cur, int pos){
//	printf("%d %d\n", cur, pos);
	if(mem[cur][pos] != 0){
		// 记忆性递归就体现在这里
		return mem[cur][pos];
	} 
	if(pos == m) return 1;
	long long ans = 0;
	if(pos%2){//cur在奇数列 
		for(int i=1; i<cur; i++){
			ans = (ans + f(i, pos+1))%MOD;
		} 
	}
	else{
		for(int i=cur+1; i<=n; i++){
			ans = (ans + f(i, pos+1))%MOD;
		}
	}
	mem[cur][pos] = ans;
	return ans;
}
int main(){
	scanf("%d%d", &m, &n);
	long long ans = 0;
	for(int i=2; i<=n; i++){
		ans = (ans + f(i, 1)) % MOD;
	}
	printf("%lld", ans);
	return 0;
} 

这个复杂度是$O(n^3)$的，因为这里遍历了n遍：

for(int i=2; i<=n; i++){
		ans = (ans + f(i, 1)) % MOD;
	}

然后$f(cur,pos)$是cur的取值范围*pos的取值范围，即$m\ast n$，估算为$O(n^2)$，合起来就是$O(n^3)$。

可以过80%的样例。

方法二：为了拿到更多分，可以每次只拆开一层。

那么这次$f(cur,pos)$的含义就变得更加大一点：

• 如果pos是奇数，就表示下一位为[1, cur-1]的摆动序列总个数
• 如果pos是偶数，就表示下一位为[cur+1, n]的摆动序列总个数

也要更改递推式了，这次只小面积的拆，只拆一层：
那么每次只拆一层是这个意思：

那么递推式变为：

• 如果$cur$在奇数列，即pos % 2 == 1：$f(cur,pos)=f(cur-1,pos)+f(cur-1,pos+1)$
• 如果$cur$在偶数列，即pos % 2 == 0：$f(cur,pos)=f(cur+1,pos)+f(cur+1,pos+1)$

【代码】

#include
using namespace std;
const int maxn = 1010;
const int MOD = 10000;
int mem[maxn][maxn];
int m, n;
long long f(int cur, int pos){
//	printf("%d %d\n", cur, pos);
	if(mem[cur][pos] != 0){
		return mem[cur][pos];
	} 
	if(pos == m) return 1;
	long long ans = 0;
	if(pos%2){
		//表示下一个数为1~cur-1的序列个数
		if(cur == 1) return 0;
		//只拆一层，拆开下一个数为cu1-1的一层 
		return mem[cur][pos] = (f(cur-1, pos) + f(cur-1, pos+1))%MOD;
	}
	else{
		//表示下一个数为cur+1~n的序列个数
		if(cur == n) return 0;
		//拆开下一个数为cur+1的一层 
		return mem[cur][pos] = (f(cur+1, pos) + f(cur+1, pos+1))%MOD;
	}
}
int main(){
	scanf("%d%d", &m, &n);
	long long ans = 0;
	ans = f(1, 0);
	printf("%lld", ans);
	return 0;
} 

9. 通电

prim算法，最小生成树，模板题。

【代码】

/*
2015年，全中国实现了户户通电。作为一名电力建设者，小明正在帮助一带一路上的国家通电。
这一次，小明要帮助 n 个村庄通电，其中 1 号村庄正好可以建立一个发电站，所发的电足够所有村庄使用。
现在，这 n 个村庄之间都没有电线相连，小明主要要做的是架设电线连接这些村庄，使得所有村庄都直接或间接的与发电站相通。
小明测量了所有村庄的位置（坐标）和高度，如果要连接两个村庄，小明需要花费两个村庄之间的坐标距离加上高度差的平方，形式化描述为坐标为 (x_1, y_1) 高度为 h_1 的村庄与坐标为 (x_2, y_2) 高度为 h_2 的村庄之间连接的费用为
sqrt((x_1-x_2)*(x_1-x_2)+(y_1-y_2)*(y_1-y_2))+(h_1-h_2)*(h_1-h_2)。
在上式中 sqrt 表示取括号内的平方根。请注意括号的位置，高度的计算方式与横纵坐标的计算方式不同。
由于经费有限，请帮助小明计算他至少要花费多少费用才能使这 n 个村庄都通电。
*/
#include
#include 
using namespace std;
const int maxn = 1010;
const double INF = 0x3fffffff;
double G[maxn][maxn];
struct node{
	int x, y, h;
}graph[maxn];
int n;
double d[maxn];
bool vis[maxn];
double prim(){
	fill(d, d+maxn, INF);
	d[0] = 0;
	double ans = 0;
	for(int i=0; i<n; i++){
		int u = -1;
		double MIN = INF;
		for(int j=0; j<n; j++){
			if((!vis[j]) && d[j] < MIN){
				u = j;
				MIN = d[j];
			}
		} 
		if(u == -1) return -1;
		vis[u] = true;
		ans += d[u];
		for(int v=0; v<n; v++){
			if( (!vis[v]) && u != v && G[u][v] < d[v]){
				d[v] = G[u][v];
			}
		}
	}
	return ans;
}
int main(){
	scanf("%d", &n);
	for(int i=0; i<n; i++){
		scanf("%d%d%d", &graph[i].x, &graph[i].y, &graph[i].h);
	} 
	for(int i=0; i<n-1; i++){
		for(int j=i+1; j<n; j++){
			double	x = pow(graph[i].x - graph[j].x, 2);
			double	y = pow(graph[i].y - graph[j].y, 2);
			double	h = pow(graph[i].h - graph[j].h, 2);
			G[i][j] = G[j][i] = sqrt(x+y)+h;
		}
	}
	double ans = prim();
	printf("%.2f", ans);
	return 0;
}

10. 植树