js实现最大子序列和的四种解法

题目

本人最近在学数据结构与算法，但是觉得看书太枯燥了，所以选择看浙江大学-数据结构精品网课的形式进行学习。刚好看到最大子序列和这一节课，现将老师讲的算法都用js实现了一遍。其中原题如下：

看不懂没关系，我们再看一下LeetCode上与之相似的题目

实现算法

• 暴力破解法。时间复杂度 T(N)=O(N^3)
• 改进的暴力破解法。时间复杂度 T(N)=O(N^2)
• 分而治之法。时间复杂度 T(N)=O(NlogN)
• 在线处理法。时间复杂度 T(N)=O(N)

实现过程

0.用于测试的数组

  arr = [-2,1,-3,4,-1,2,1,-5,4];    //最大值6
  arr2 = [-1,-2,10,-4,-1,5,9,-10,1];//最大值19
  arr3 = [6,-3,-2,7,-15,1,2,2];     //最大值8
  arr4 = [-1,-1,-1,-1]              //最大值0

1.暴力破解法
主要根据原题求和符号上下标i，j，k的范围实现暴力破解算法

export default (arr)=>{
  let sumTmp = 0;
  let sumMax = 0;
  let max = arr.length;
  for(let i=0;i<max;i++){
    for(let j=i;j<max;j++){
      for(let k=i;k<j;k++){
        sumTmp += arr[k];
      }
      if(sumTmp>0&&sumTmp>sumMax){
        sumMax = sumTmp;
      }
      sumTmp = 0;
    }
  }
  return sumMax;
}

2.改进的暴力破解法
认真思考，其实k是无需考虑的，只需考虑i，j的范围即可

export default (arr)=>{
  let sumTmp = 0;
  let sumMax = 0;
  let max = arr.length;
  for(let i=0;i<max;i++){
    for(let j=i;j<max;j++){
      sumTmp += arr[j];
      if(sumTmp>0&&sumTmp>sumMax){
        sumMax = sumTmp;
      }
    }
    sumTmp = 0;
  }
  return sumMax;
}

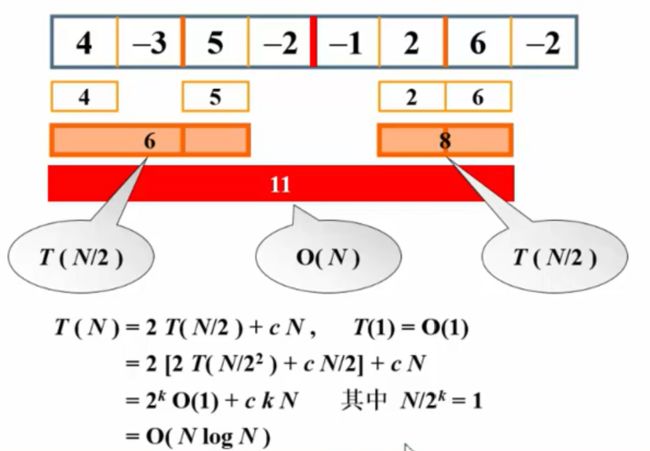
3.分而治之法
因为网上已经有很多文章讲解分而治之法，这里就不加赘述了。

export default (arr)=>{
  function maximumItemSum(array,leftest,rightest){
    //递归只剩下一项
    if(leftest == rightest) {  
      return array[rightest]>0?array[rightest]:0
    }else{
      let middle = Math.floor((leftest+rightest)*0.5); //相除之后向下取整,求得中间分割线
      //左侧的最大子序列  
      let maxLeftSum = maximumItemSum(arr, leftest, middle);  
      //右侧的最大子序列
      let maxRightSum = maximumItemSum(arr, middle+1, rightest);  

      //中线左边求和。
      let sumLeftTmp = 0; //暂存左边累加的结果
      let maxBorderLeft = 0;  //用于存储分割线左边和的最大值
      for(let i=middle;i>=leftest;i--){
        sumLeftTmp +=array[i];
        if(sumLeftTmp>maxBorderLeft){
          maxBorderLeft = sumLeftTmp;
        }
      }

      //中线右边求和。
      let sumRightTmp = 0;//暂存右边累加的结果
      let maxBorderRight = 0; //用于存储分割线右边的最大值
      for(let j=middle+1;j<=rightest;j++){
        sumRightTmp +=array[j];
        if(sumRightTmp>maxBorderRight){
          maxBorderRight =sumRightTmp;
        }
      }

      //取出最大的值
      let maxSum = Math.max(maxLeftSum,maxRightSum,maxBorderLeft+maxBorderRight);
      return maxSum
    }      
  }
  console.log('maxSum:',maximumItemSum(arr,0,arr.length-1));
  return maximumItemSum(arr,0,arr.length-1);
}

这里要注意的是求该算法的时间复杂度，求解过程如下。实在不懂得，可以点击前文的视频链接，自行观看推导过程。

4.在线处理法
其中，“在线”的意思是指每输入一个数据就进行及时处理，在任何一个地方终止输入，算法都能给出当前的解。代码如下：

function onlineDeal(arr,len){
  let maxSum=0,tmpSum = 0;     //maxSum存储最终的sum,tmpSum为累加过程中暂存sum
  console.log(maxSum,tmpSum);
  for(var i=0;i<len;i++){
    tmpSum += arr[i];
    tmpSum>maxSum?maxSum=tmpSum:maxSum
    tmpSum<0?tmpSum=0:tmpSum;
  }
  console.log('最大子序列和:',maxSum);
}
onlineDeal(arr,arr.length)

具体实现过程如下

以数组[-1,3,-2,4,-6,1,6,-1]为例，数组从第一项开始从左向右累加，
第一次累加：tmpSum=-1；最大子序列maxSum=0；因tmpSum<0，所以tmpSum清空；
第二次累加：tmpSum=3；最大子序列maxSum=3；
第三次累加：tmpSum=1；最大子序列maxSum=3；
第四次累加：tmpSum=5；最大子序列maxSum=5；
第五次累加：tmpSum=-1；最大子序列maxSum=5；因tmpSum<0，所以tmpSum清空；
第六次累加：tmpSum=1；最大子序列maxSum=5；
第七次累加：tmpSum=7；最大子序列maxSum=7；
第八次累加：tmpSum=6；最大子序列和maxSum=7；