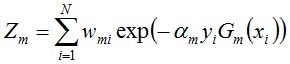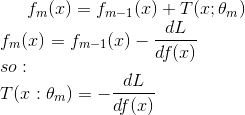数据挖掘-集成学习

 

1.集成学习概念：

•    个体学习器通常是用一个现有的学习算法从训练数据产生，例如C4.5决策树算法、BP神经网络算法等。此时集成中只包含同种类型的个体学习器，例如“决策树集成”中的个体学习器全是决策树，“神经网络集成”中就全是神经网络，这样的集成是“同质”（homogeneous）的，同质集成中的个体学习器也称为“基学习器”（baselearner），相应的学习算法称为“基学习算法”（baselearning algorithm）。有同质就有异质（heterogeneous），若集成包含不同类型的个体学习器，例如同时包含决策树和神经网络，那么这时个体学习器一般不称为基学习器，而称作“组件学习器”（componentleaner）或直接称为个体学习器。

2.为什么要集成：

•1）模型选择

•假设个弱分类器将具有一定的差异性，这会导致生成的分类决策边界不同，也就是说他们在决策 的时候会犯不同的错误。将他们结合后能得到更合理的边界，减少整体的错误， 实现更好的分类效果。

•2）数据集过大或过小

•数据集过大时，可以分成不同的子集，分别训练，再合成分类器。

•数据集过小时，可采用有放回抽样（bootstrap）

•3）数据融合（datafusion）

•当有多个不同的数据源时，且每个数据源的特征集抽取的方法不同时，需要分别训练再集成

3.hard voting  和  soft voting:

hard voting 是依据投票进行决策

soft voting 是依据各分类器的概率之和 进行决策

#coding=gbk
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

x, y = datasets.make_moons(n_samples=500, random_state=42, noise =0.3)
print(x[:10,:10])
print(x.shape,' ',y.shape)  #(500, 2)   (500,)
print(y[:10])       #[1 0 1 0 0 1 1 0 0 1]  输出两类数据集

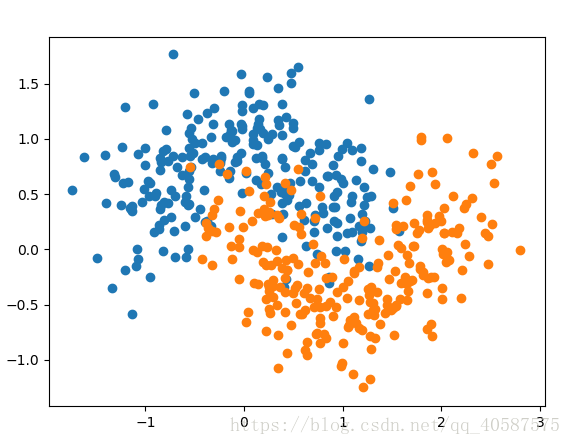
plt.scatter(x[y==0,0],x[y==0,1])        #画出 label y==0 这一行的数据，输出行列数据
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()      #  自定义一个数据集

当 noise 噪声为 0 时，显示是两个半圆的数据集

当噪声 noise 为 0.3 的数据集,画出图像为：

 

 

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0)

from sklearn.linear_model import LogisticRegression #使用逻辑回归
clf = LogisticRegression()
clf.fit(x_train, y_train)
clf_score = clf.score(x_test, y_test)
print(clf_score)        #  0.832

from sklearn.svm import SVC     #使用支持向量机
svm = SVC()
svm.fit(x_train, y_train)
svm.score = svm.score(x_test, y_test)
print(svm.score)    #   0.84

from sklearn.tree import DecisionTreeClassifier     #使用决策树
tree = DecisionTreeClassifier()
tree.fit(x_train, y_train)
tree_score = tree.score(x_test, y_test)
print(tree_score)       #0.808

#使用投票法集成学习
y_predict1 = clf.predict(x_test)
y_predict2 = svm.predict(x_test)
y_predict3 = tree.predict(x_test)
y_predict = np.array((y_predict1 + y_predict2 +y_predict3) >=2,dtype='int')
print(y_predict[:10])       #[1 1 0 1 0 1 1 1 1 0]投票法预测的结果

from sklearn.metrics import accuracy_score
all_score = accuracy_score(y_test, y_predict)
print(all_score)        #  0.848    正确率有所提升

#使用sklearn 中的voting classifier
from sklearn.ensemble import VotingClassifier
voting_clf = VotingClassifier([
    ('log_clf', LogisticRegression()),
    ('svm_clf',SVC()),
    ('tree_clf',DecisionTreeClassifier())
    ],voting= 'hard')
voting_clf.fit(x_train, y_train)
voting_score = voting_clf.score(x_test, y_test)
print(voting_score)     #0.848  和上述的预测结果是一样的， ‘hard’ 代表是投票机制,依据票数决定

#依据权重进行投票,为soft voting 计算每个模型概率的和    predict_proba,
#KNN 和逻辑回归  ， 决策树 (svc也可以取得其概率  probability = True)
soft_voting_clf = VotingClassifier([
    ('log_clf',LogisticRegression()),
    ('svm_clf',SVC(probability=True)),      #因为 soft voting 是依据概率来进行决策的， 所以需要是probability 为True
    ('tree_clf',DecisionTreeClassifier(random_state= 666, max_depth=8))
    ],voting = 'soft')
soft_voting_clf.fit(x_train, y_train)
soft_voting_score = soft_voting_clf.score(x_test, y_test)
print('soft_voting_score is %.4f'%soft_voting_score)    #  soft_voting_score is 0.8560

---

4.集成学习常用算法（Boosting, Bagging, Stacking（暂时不考虑，和神经网络有相似之处））

•目前集成学习方法大致可分为两大类：

第一类是个体学习器之间存在强依赖关系、必须串行生成的序列化方法，这种方法的代表是“Boosting”；

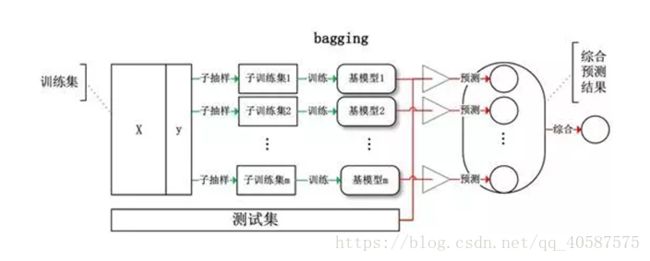
第二类是个体学习器间不存在强依赖关系、可同时生成的并行化方法，它的代表是“Bagging”和“RandomForest”

•Bagging:bagging通过降低基分类器方差改善了泛化能力，因此bagging的性能依赖于基分类器的稳定性，如果基分类器是不稳定的，bagging有助于减低训练数据的随机扰动导致的误差，但是如果基分类器是稳定的，即对数据变化不敏感，那么bagging方法就得不到性能的提升，甚至会减低，因为新数据集只有63%。最常用的是DT决策树

 

•随机森林（RandomForest）是许多决策树的平均，每个决策树都用通过Bootstrap的方式获得随机样本训练。森林中的每个独立的树都比一个完整的决策树弱，但是通过将它们结合，可以通过多样性获得更高的整体表现。

•随机森林具有Self-testing的特性，因为随机森林是通过Bootstrap的方式采样，理论上往往会有大约1/3的原始数据没有被选中，我们叫做OOB（outof bag），而这部分数据刚好可以用来做测试，类似于Cross-Validation的作用。一般的基础分类器的个数为500棵或者可以更多。非参数的机器学习算法对个别的数据点较为敏感。

 

1•随机森林具有很多的优点：

•所有的数据都能够有效利用，而且不用人为的分出一部分数据来做cross-validation；

•随机森林可以实现很高的精确度，但是只有很少的参数，而且对于分类和回归都适用；

•不用担心过拟合的问题；

•不需要事先做特征选择，每次只用随机的选取几个特征来训练树。

2•它的缺点是：

•相比于其他算法，其输出预测可能较慢。

 

使用bagging 和 randomforest ：

#coding=gbk
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

x, y = datasets.make_moons(n_samples=500, random_state=42, noise =0.3)
print(x[:10,:10])
print(x.shape,' ',y.shape)  #(500, 2)   (500,)
print(y[:10])       #[1 0 1 0 0 1 1 0 0 1]  输出两类数据集

plt.scatter(x[y==0,0],x[y==0,1])        #画出 label y==0 这一行的数据，输出行列数据
plt.scatter(x[y==1,0],x[y==1,1])
# plt.show()

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y,random_state=666)

#使用bagging 有放回取样 
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier

bagging_clf = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators= 50,max_samples = 100,    #n_estimators 子模型的数量
                                bootstrap = True)
bagging_clf.fit(x_train, y_train)
bagging_score = bagging_clf.score(x_test, y_test)
print(bagging_score)            #  0.872        #当estimators 为5000时，还是一样

#使用 oob_score = True  依据统计学，可能还有37% 的数据未抽到， 可将其作为测试集
bagging_clf2 = BaggingClassifier(DecisionTreeClassifier(),
                                n_estimators= 50,max_samples = 100,    #n_estimators 子模型的数量
                                bootstrap = True, oob_score= True)  #增加 oob_score =True
bagging_clf2.fit(x_train, y_train)
bagging_oob_score = bagging_clf2.oob_score_
print(bagging_oob_score)            #  0.9306666666666666  很不错的数据

#bootstrap_features 为True 时， max_samples 既对数据进行随机抽样， 也对特征进行随机抽样
#使用  n_jobs  还可以进行并行处理
bagging_patches_clf = BaggingClassifier(DecisionTreeClassifier(),
                                        n_estimators=500, max_samples=100,bootstrap = True,
                                        max_features=1, bootstrap_features = True,random_state=666,
                                        oob_score = True)
bagging_patches_clf.fit(x_train, y_train)
patches_score = bagging_patches_clf.oob_score_
print(patches_score)            #  0.888

#使用随机森林, RandomForest  决策树在结点的划分上， 在随机的特征子集上， 寻找最优划分特征
print(' using randomForest')
from sklearn.ensemble import RandomForestClassifier
rf_clf = RandomForestClassifier(n_estimators=500, random_state = 666, oob_score=True, n_jobs=True)
rf_clf.fit(x_train, y_train)
print(rf_clf.oob_score_)    #  0.9253333333333333

#Extra - Trees, 极度随机决策树, 在决策树的结点划分上， 使用随机的特征和随机的阈值， 
#提供额外的随机性， 抑制过拟合， 当增大了bias 
#用于比随机森林更快的训练速度
from sklearn.ensemble import ExtraTreesClassifier
er_clf = ExtraTreesClassifier(n_estimators=500, random_state=666, oob_score=True, 
                              bootstrap= True, n_jobs=-1)
er_clf.fit(x,y)
print(er_clf.oob_score_)        # 0.892

 

•boosting：提升方法是一个迭代的过程，通过改变样本分布，使得分类器聚集在那些很难分的样本上，对那些容易错分的数据加强学习，增加错分数据的权重，这样错分的数据再下一轮的迭代就有更大的作用（对错分数据进行惩罚）。数据的权重有两个作用，一方面我们可以使用这些权值作为抽样分布，进行对数据的抽样，另一方面分类器可以使用权值学习有利于高权重样本的分类器。

 

•AdaBoost（adaptive  boosting）会根据当前的错误率，按照增大错误样本权重，减小正确样本权重的原则更新每个样本的权重。不断重复训练和调整权重，直到训练错误率或基学习器的个数满足用户指定的数目为止。Adaboost的最终结果为每个弱学习器加权的结果。

•AdaBoost优点：

•很容易实施

•几乎没有参数需要调整

•不用担心过拟合

 

•缺点：

•公式中的α是局部最优解，不能保证是最优解

•对噪声很敏感

 

•Gradient  Boosted Regression Trees (GBRT)梯度提升回归树：

•GBRT也是一种Boosting方法，每个子模型是根据已训练出的学习器的性能(残差)训练出来的，子模型是串行训练获得，不易并行化。GBRT基于残差学习的算，没有AdaBoost中的样本权重的概念。GBRT结合了梯度迭代和回归树，准确率非常高，但是也有过拟合的风险。GBRT中迭代的是残差的梯度，残差就是目前结合所有得到的训练器预测的结果与实际值的差值。

 

使用AdaBoost  和 Gradient Boosting 梯度提升：

#coding=gbk
#使用 ada_boosting 
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

x, y = datasets.make_moons(n_samples=500, random_state=42, noise =0.3)
print(x[:10,:10])
print(x.shape,' ',y.shape)  #(500, 2)   (500,)
print(y[:10])       #[1 0 1 0 0 1 1 0 0 1]  输出两类数据集

plt.scatter(x[y==0,0],x[y==0,1])        #画出 label y==0 这一行的数据，输出行列数据
plt.scatter(x[y==1,0],x[y==1,1])
# plt.show()

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y)
ac_clf = AdaBoostClassifier(DecisionTreeClassifier(max_depth=4), n_estimators=500, random_state= 666)
                            
ac_clf.fit(x_train, y_train)
score = ac_clf.score(x_test, y_test)
print(score)        #    0.928

# Gradient Boosting 梯度提升
#训练一个模型 m1 ，产生 错误e1， 针对e1 训练第二个模型m2 ，产生错误e2 继续训练下去，直到达到条件
from sklearn.ensemble import GradientBoostingClassifier
gb_clf = GradientBoostingClassifier(max_depth=5, n_estimators=500)
gb_clf.fit(x_train, y_train)
score1 =gb_clf.score(x_test, y_test)
print(score1)       #  0.88

Adaboost的优缺点：

Adaboost的主要优点有：

　　　　1）Adaboost作为分类器时，分类精度很高

　　　　2）在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活。

　　　　3）作为简单的二元分类器时，构造简单，结果可理解。

　　　　4）不容易发生过拟合

Adaboost的主要缺点有：

　　　　1）对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。

GDBT的优缺点：

GBDT主要的优点有：

　　　　1) 可以灵活处理各种类型的数据，包括连续值和离散值。

　　　　2) 在相对少的调参时间情况下，预测的准确率也可以比较高。这个是相对SVM来说的。

　　　　3）使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。

GBDT的主要缺点有：

　　　　1)由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。

随机森林优缺点：

RF的主要优点有：

　　　　1） 训练可以高度并行化，对于大数据时代的大样本训练速度有优势。个人觉得这是的最主要的优点。

　　　　2） 由于可以随机选择决策树节点划分特征，这样在样本特征维度很高的时候，仍然能高效的训练模型。

　　　　3） 在训练后，可以给出各个特征对于输出的重要性

　　　　4） 由于采用了随机采样，训练出的模型的方差小，泛化能力强。

　　　　5） 相对于Boosting系列的Adaboost和GBDT， RF实现比较简单。

　　　　6） 对部分特征缺失不敏感。

RF的主要缺点有：

　　　　1）在某些噪音比较大的样本集上，RF模型容易陷入过拟合。

　　　　2) 取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果。

 

 Xgboost与GDBT原理的区别：

       XGBoost的性能在GBDT上又有一步提升，而其性能也能通过各种比赛管窥一二。坊间对XGBoost最大的认知在于其能够自动地运用CPU的多线程进行并行计算，同时在算法精度上也进行了精度的提高。 
　　由于GBDT在合理的参数设置下，往往要生成一定数量的树才能达到令人满意的准确率，在数据集较复杂时，模型可能需要几千次迭代运算。但是XGBoost利用并行的CPU更好的解决了这个问题。
 

1. 传统的GBDT以CART树作为基学习器，XGBoost还支持线性分类器，这个时候XGBoost相当于L1和L2正则化的逻辑斯蒂回归（分类）或者线性回归（回归）；
2. 传统的GBDT在优化的时候只用到一阶导数信息，XGBoost则对代价函数进行了二阶泰勒展开，得到一阶和二阶导数；
3. XGBoost在代价函数中加入了正则项，用于控制模型的复杂度。从权衡方差偏差来看，它降低了模型的方差，使学习出来的模型更加简单，放置过拟合，这也是XGBoost优于传统GBDT的一个特性；
4. shrinkage（缩减），相当于学习速率（XGBoost中的eta）。XGBoost在进行完一次迭代时，会将叶子节点的权值乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。（GBDT也有学习速率）；
5. 列抽样。XGBoost借鉴了随机森林的做法，支持列抽样，不仅防止过 拟合，还能减少计算；
6. 对缺失值的处理。对于特征的值有缺失的样本，XGBoost还可以自动 学习出它的分裂方向；
7. XGBoost工具支持并行。Boosting不是一种串行的结构吗?怎么并行 的？注意XGBoost的并行不是tree粒度的并行，XGBoost也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。XGBoost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），XGBoost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代 中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。

原文：https://blog.csdn.net/qq_28031525/article/details/70207918 
 

AdaBoost 原理推导：

wil的笔记  的 blog中有个关于adaboost 的计算例子，十分有助于我们对adaboost的理解。

文中例子  ‘第二轮’中的Z1 表示：（就是全部新的权重因子的和，称为规范化因子，使其全部权重相加为1 .）

AdaBoost算法可以认为是一种模型为加法模型、损失函数为指数函数、学习算法为前向分步算法的而分类学习方法。

前向分步算法对加法模型的求解思路是：如果能够从前向后，每一步只学习一个基函数及其系数，逐步逼近优化目标，那么就可以简化优化的复杂度。

1.  的推导过程：

AdaBoost算法是前向分布加法算法的特例。这时，模型是由基本分类器组成的加法模型，损失函数是指数函数。即此时的基函数为基分类器。AdaBoost的最终分类器为：

                                                

定义损失函数为：

                                -------1

当真实值与预测值不同时，损失值为 e ，相同时为1/e

 

进行 t 轮的迭代可得：

                                        -----2

我们的目标是求得   和  使得损失函数最小，将式2 带入到式1 当中：

 

其中：  ，其均不依赖于    和   ，只与   ，会随着每一轮的迭代而发生变化。

对式子进行变形：

 

对式子   进行求导：

先令 ：

                 

可以得到：

                

由此知道：

αt  随着et  的减小而增大，所以分类误差率越小的基分类器在最终分类器中的作用越大。

 

2.  的推导：

由上述推导的式子：

                            

将第一个式子两边 同时乘以   ，并作为 e 的指数，可以得到：

                                                                        

再添加一个分母进行规范化：

                                  
                                                    

 

GBDT(Gradient Boosting Decision Tree):梯度提升树：

 

梯度提升树中负梯度和残差的关系：

我们希望找到一个使每次都对提升树进行提升，使得损失函数达到最小。

即找到最好的决策树对负梯度（残差是负梯度的一种特例）进行拟合。

GBDT回归算法流程：

算法步骤解释：

1. 初始化，估计使损失函数极小化的常数值，它是只有一个根节点的树，即 ganma 是一个常数值。（可以为全部y值的平均值）
2. 迭代 
   a. 计算损失函数的负梯度在当前模型的值，将它作为残差的估计 
   b. 估计回归树叶节点区域，以拟合残差的近似值 
   c. 利用线性搜索估计叶节点区域的值，使损失函数极小化 （这里不同于传统的CART回归树叶子结点值取平均值作为输出值，gbdt的Cart树是依据损失函数极小化来决定叶子的结点值的）
   d. 更新回归树
3. 得到输出的最终模型 f(x)

GBDT分类：

在分类训练的时候，是针对样本 X 每个可能的类都训练一个分类回归树。

针对样本有三类的情况，我们实质上是在每轮的训练的时候是同时训练三颗树。第一棵树针对样本 x 的第一类，输入为（x, 0）。

第二棵树输入针对样本 x 的第二类，假设 x 属于第二类，输入为（x, 1）。

第三棵树针对样本 x 的第三类，输入为（x, 2）。在这里每棵树的训练过程其实就是就是我们之前已经提到过的 CART 的生成过程。依据生成分类树的流程即可以就解出三棵树，以及三棵树对 x 类别的预测值 f1(x), f2(x), f3(x)。

那么在此类训练中，我们仿照多分类的逻辑回归，使用 softmax 来产生概率。

并且我们我们可以针对类别 1 求出残差 f11(x) = 0 − f1(x)；类别 2 求出残差 f22(x) = 1 − f2(x)；类别 3 求出残差 f33(x) = 0 − f3(x)。然后开始第二轮训练，针对第一类输入为(x, f11(x))，针对第二类输入为(x, f22(x))，针对第三类输入为(x, f33(x))。继续训练出三棵树，一直迭代 M 轮，每轮构建 3 棵树。当训练完毕以后，新来一个样本 x1，我们需要预测该样本的类别的时候，便可使用 softmax 计算每个类别的概率。

仿照多分类的逻辑回归，使用softmax来产生概率，则属于某个类别c的概率为

 

 

参考： https://www.cnblogs.com/willnote/p/6801496.html
             https://blog.csdn.net/ruiyiin/article/details/77114072

             https://blog.csdn.net/qq_32690999/article/details/78759463

 

adaboost算法原理参照：

                             https://www.cnblogs.com/willnote/p/6801496.html
                             https://blog.csdn.net/v_july_v/article/details/40718799

GBDT算法原理参考：

                          https://www.cnblogs.com/pinard/p/6140514.html

Xgboost算法参考：

                           https://www.jianshu.com/p/7467e616f227