机器学习 复习笔记2 （第二章 模型选择与评估）

2.1 经验误差与过拟合

错误率的概念：分类错误的样本占样本总数的比例：E=a/m

误差的概念：学习器的实际预测输出与样本真实输出之间的差异称为误差。误差分为三种：

1. 训练（经验）误差：学习器在训练集上的误差（实际中只能做到此项上的最小）
2. 测试误差：学习器在测试集上的误差
3. 泛化误差：学习器在新样本上的误差（此项越小则学习器效果越好）

过拟合：学习器把训练样本学习得太好，将训练样本本身得特点当成所有样本一般性质，导致泛化性能下降。克服方法：优化目标加正则项，提前停止训练。

欠拟合：对训练样本的一般性质尚未学好。克服方法：拓展分支（对于决策树），增加训练轮数（神经网络）。

2.2 评估方法

通过实验测试来对学习器的泛化误差进行评估并进而做出选择

留出法：

留出法适合数据量大、允许一定精度损失的情况

• 直接将数据集划分为两个互斥集合
• 训练/测试集划分尽可能保持数据分布的一致性（例如对D进行分层采样而获得70%样本的训练集S和含30%样本的测试集，若D包含500个正例、500个反例，则S应包含350个正例、350个反例）
• 一般若干次随机划分、重复实验取平均值
• 训练/测试样本的比例通常为2：1~4：1

交叉验证法

将数据集分层采样划分为k个大小相似的互斥子集，每次利用k-1个子集的并集作为训练集，余下的子集为测试集，最终返回k个测试结果的均值，k最常用的取值是10.

与留出法类似，若将数据集D划分为k个子集同样存在多种划分方式，为了减少印样本划分不同而引入的差别，k率交叉验证通常采用不同的划分方式重复p次最终的评估结果是这p次k折交叉验证结果的均值，例如常见的“10次10折交叉验证”。

假定数据集D包含m个样本，若令k=m，则得到留一法，留一法具有以下特点：

• 不受随机样本划分方式的影响
• 结果往往比较准确
• 当数据集比较大时开销难以接受

交叉验证法比较适合数据量较小时使用。

相关题目：

数据集中包含100个样本，其中正反例各一半，假定学习算法所产生的模型是将新样本预测为训练样本较多的类别（训练样本数相同时进行随机猜想），试给出10折交叉验证法和留一法分别对错误率进行评估所得的结果。

答：对于10折交叉验证法，每次训练集中正反例数目都一样，所以判断为正反例的概率也是一样的，错误率的期望是50%；对于留一法，留下的不管是正例还是反例，总会使训练集中，另外一种例子多一个，因此最终错误率是100%。

 自助法

给定m个数据的数据集D，对它采样生成数据集D',然后再将样本放回到原始数据集D中，使得该样本在下次采样时仍有可能被采到；这个过程执行m次后，就得到包含m个样本的数据集D‘，这就是自主采样的结果。样本在m次采样中始终不被采到的概率是,取极限得.这样，我们得到了训练集D'，以及测试集D\D'(\为集合减法符号)。其特点可归纳为：

• 实际模型与预期模型都使用m个训练样本
• 约有1/3的样本没在训练集中出现
• 从初始数据集中产生多个不同的训练集，对集成学习有很大的好处
• 自助法在数据集较少、难以有效划分训练/测试集时很有用；由于改变了数据集分布可能引入估计偏差，在数据量足够时，留出法和交叉验证法更常用

2.3 性能度量

性能度量是衡量模型泛化能力的评价标准，反映了任务需求；使用不同的性能度量往往会导致不同的评判结果。根据度量的任务分，性能度量可以分为两大类。

对回归任务度量：均方误差

对分类任务度量：错误率、精度、查准率、查全率、查准-查全(P-R曲线)、受试者工作特征(ROC曲线)等

错误率与精度

错误率：分类错误样本占总样本数的比例

精度：分类正确的样本占样本总数的比率

查准率、查全率与F1

将样例根据其真实类别与学习器预测类别的组合划分为真正例、假正例、真反例、假反例折四种情况，令TP、FP、TN、FN分别表示对应的样例数，则查准率P与查全率R分别定义为：

    ->查准率即输出的真正例在所有输出正例中的比例

    ->查全率即输出的真正例在实际正例中的比例

PR在大多数形况下难以兼得。

根据学习器的预测结果按正例可能性大小对样例进行排序、并逐个把样本作为正例进行预测，则可以得到查准-查全率曲线，简称“P-R曲线”。

平衡点（BEP）是曲线上“查准率=查全率”时的取值，可以用来度量P-R曲线有交叉的分类器性能的高低。

P-R曲线的比较：若一个学习器的曲线完全被另一个学习器“包住”则后者的性能更优，若两学习器的曲线相交，则比较两学习器平衡点，平衡点更大的性能更优。

在一些情况下BEP还过于简单，常用的是F1，F1是基于查准率与查重率的调和平均：.

而还有一种比F1更好的形式,是加权调和平均,β>1对查全率有更大的影响，β<1对查准率有更大的影响。

ROC与AUC

类似P-R曲线，根据学习器的预测结果对样例排序，并逐个为正例进行预测，以“假正例率”为横轴，“真正例率”为纵轴可以得到ROC曲线，全程为“受试者工作特征”。

    ->真正例率即输出的真正例在实际正例中的比例，数值同查全率R。

    ->假正例率即输出的假正例在实际反例中的比例。

ROC面积下的曲线(Area Under ROC Curve):如字面上含义，简称AUC。

某个学习器的ROC曲线被另一个学习器的曲线“包住”，则后者性能优于前者；如果曲线交叉，可以根据AUC的大小进行比较，AUC值越大性能越好。

2.4 比较检验

直接进行性能比较存在的问题：

• 测试集上的性能并不等于泛化性能
• 测试集性能会随着测试集的变化而变化
• 机器学习算法本身具有一定的随机性

Friedman检验与Nemeyi后续检验

Friedman检验流程：

1. 通过算法比较序值表计算出变量
2. 根据上述步骤的出的结果，进一步算出
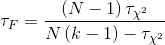
3. 在F检验的常用临界值表中找到对应的临界值与上述值进行比较，若表中临界值更小，则拒绝“所有算法洗呢能都相同”这个假设，进而进行后续检验。

其中，N是数据集个数，k为算法个数，为对应算法的平均序值。

Nemeyi后续检验流程：

1. 通过Nemenyi检验常用值表找到计算需要的值。
2. 带入公式计算出临界值域
3. 若两个算法平均序值之差超过了临界值域CD，则以响应的置信度拒绝“两个算法性能相同”这一假设。

Friedman检验图绘制流程：

1. 图形的横坐标是平均序值，纵坐标是不同算法
2. 每个算法原点为其平均序值，线段为临界阈值的大小

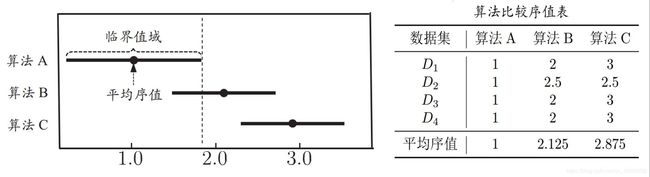检验图图例

若两个算法有交叠，则说明没有现主差别，否者有显著差别，图形越靠左算法越优越。