数字图像处理第三版(冈萨雷斯)——第三章灰度变换与空间滤波(part1)
数字图像处理第三版(冈萨雷斯)——第三章灰度变换与空间滤波part1
- 引言
- 3.1 背景知识
- 3.1.1 灰度变换和空间滤波基础
- 3.2 灰度变换
- 3.2.1 图像反转
- 3.2.2 对数变换
- 3.2.3 幂律(伽马)变换
- 3.2.4 分段线性变换函数
- 3.3 直方图处理
- 3.3.1 直方图均衡
- 3.3.2 直方图匹配(规定化)
- 3.3.3 局部直方图处理
- 3.3.4 在图像增强中使用直方图统计
- 3.4 空间滤波基础
- 3.4.1 ==空间滤波机理==
- 3.4.2 空间相关与卷积
- 3.4.3 线性滤波的向量表示
- 3.4.4 空间滤波器模板的产生
引言
空间域(相对于变换域而言)指图像平面本身,该类图像处理方法直接操作图像中的像素。
空间域处理主要分为两类:灰度变换、空间滤波
(1) 灰度变换:对图像的单个像素进行操作,以对比度和阈值处理为目的;
(2) 空间滤波:涉及改善性能的操作。如通过图像中每个像素的邻域处理来锐化图像。
3.1 背景知识
3.1.1 灰度变换和空间滤波基础
- 通常,空间域技术在计算上更有效,且执行所需的处理资源较少。
- 空间域处理可表示为:
g ( x , y ) = T [ f ( x , y ) ] g(x,y)=T[f(x,y)] g(x,y)=T[f(x,y)]
f ( x , y ) f(x,y) f(x,y)为输入图像, g ( x , y ) g(x,y) g(x,y)为输出图像, T T T为点 ( x , y ) (x,y) (x,y)邻域上定义的关于 f f f的一种算子。

f i g u r e 1 figure1 figure1 - 邻域:通常是中心在(x,y)的矩形,其尺寸比图像小得多
- 空间滤波过程:
正如 f i g u r e 1 figure1 figure1所示,邻域原点从一个像素向另一个像素移动,对邻域中像素应用算子T,并在该位置输出。如此,对应于任意指定位置(x,y),对其邻域应用算子T,得到的结果即为输出图像g在这些坐标的值。下面选取一点进行说明(假设邻域原点位于邻域中心,采取3*3均值滤波器进行说明):
从f任意选取一点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),则在该位置输出 g ( x 0 , y 0 ) g(x_0,y_0) g(x0,y0)的值为,计算 f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0)和其8个邻点的和再除以9(即由邻域包围的像素灰度的平均值)。然后邻域原点移动到下一位置重复此过程产生下一个输出像素的值,直到对f中所有像素进行完此操作,便可得到图像g。
空间滤波像素处理顺序通常从输入图像的左上角开始,以水平扫描的方式逐像素地处理,每次一行。当该邻域的原点位于图像的边界上时,部分邻域将位于图像的外部。此时,在用T做指定点的计算时,或者忽略外侧邻点,或者用0或其他指定的灰度值填充图像的边界(边界填充,也称边界延拓)。被填充边界的厚度取决于模板(邻域)的大小。 - 常见边界填充方式如下:


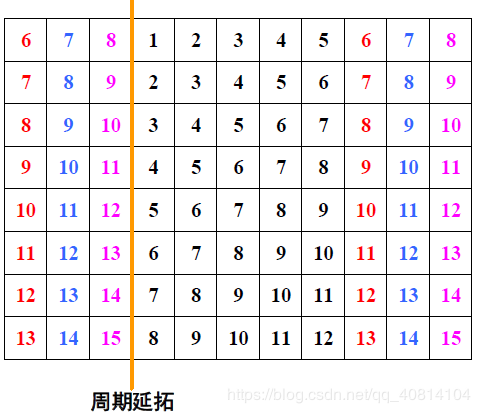
- 空间滤波器
邻域与预定义的操作一起成为空间滤波器(也称为空间掩模、核、模板、窗口)
The process that Fig. 3.1 illustrates consists of moving the origin of the neighborhood from pixel to pixel and applying the operator T to the pixels in the neighborhood to yield the output at that location.Thus, for any specific location (x, y), the value of the output image g at those coordinates is equal to the result of applying T to the neighborhood with origin at (x, y) in f. For example, suppose
that the neighborhood is a square of size 3*3 and that operator T is defined as “compute the average intensity of the neighborhood.” Consider an arbitrary location in an image, say (100, 150). Assuming that the origin of the neighborhood is at its center, the result,g(100,150) , at that location is computed
as the sum of and its 8-neighbors, divided by 9 (i.e., the average intensity of the pixels encompassed by the neighborhood). The origin of the neighborhood is then moved to the next location and the procedure is repeated to generate the next value of the output image g.Typically, the process starts at the top left of the input image and proceeds pixel by pixel in a horizontal scan, one row at a time.When the origin of the neighborhood is at the border of the image, part of the neighborhood will reside outside the image.The procedure is either to ignore the outside neighbors in the computations specified by T, or to pad the image with a border of 0s or some other specified intensity values.The thickness of the padded border depends on the size of the neighborhood.We will return to this issue in Section 3.4.1.
As we discuss in detail in Section 3.4, the procedure just described is called spatial filtering, in which the neighborhood, along with a predefined operation, is called a spatial filter (also referred to as a spatial mask, kernel, template, or window). The type of operation performed in the neighborhood determines the nature of the filtering process.
- 对比度拉伸
在最小邻域(大小为1×1)情况下,T成为一个灰度变换函数:
s = T ( r ) s=T(r) s=T(r)
其中,r和s分别表示g和f 在任意点(x,y)处的灰度。

对 比 度 拉 伸 函 数 对比度拉伸函数 对比度拉伸函数
如图所示,低于k的灰度级更暗,而高于k的灰度级更亮。这种技术称为对比度拉伸,经过对比度拉伸变换后,得到的灰度图像将比原始图像有更高的对比度。 - 阈值处理函数

阈 值 处 理 函 数 阈值处理函数 阈值处理函数
如图所示的极限情况, T ( r ) T(r) T(r)产生一幅两级(二值)图像。 - 本章主要使用灰度变换函数来增强图像。第10章将使用灰度变换函数来分割图像。
图像增强:不考虑图像降质的原因,只将图像中感兴趣的特征有选择地突出,对不需要的特征进行衰减。增强技术是面向问题的。
目的:
1)改善图像视觉效果,便于观察和分析;
2)便于人工或机器对图像的进一步处理
- 点处理技术:输出图像中,每个像素的灰度仅取决于输入图像中相应的一个点的灰度。
- 邻域处理技术:输出图像中,每个像素的灰度是由对应的输入像素的灰度及其相应邻域内的像素灰度共同决定的。
3.2 灰度变换
- 灰度变换是所有图像处理技术中最简单的技术。由于我们处理的是数字图像,所以,变换函数的值通常存储在一个一维阵列中,且从r到s的映射是通过查找表实现从输入像素到输出像素的映射。
- 图像增强常用的三类基本函数
线性函数(反转和恒等变换)
对数函数(对数和反对数变换)
幂律函数(n次幂和n次根变换)
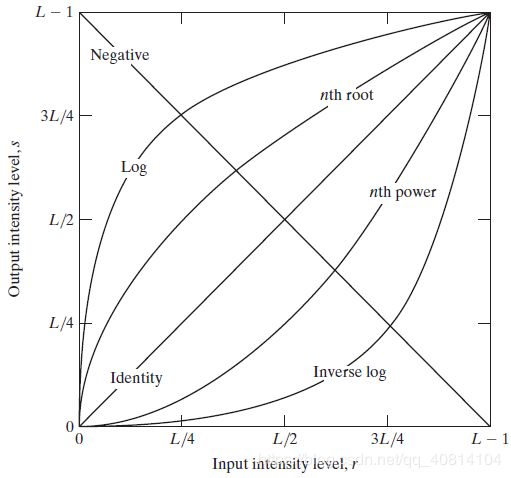
3.2.1 图像反转
公式:
s = L − 1 − r , L 为 灰 度 级 数 ( 即 l m a x ) {s=L-1-r}\quad,L为灰度级数(即l_{max}) s=L−1−r,L为灰度级数(即lmax)
图像反转:反转一幅图像的灰度级,可得到等效的照片底片。特别适用于增强嵌入图像暗色区域中的白色或灰色细节,特别是当黑色面积在尺寸上占主导地位时。如:

3.2.2 对数变换
公式:
s = c l o g ( 1 + r ) , c 是 常 数 , 并 假 设 r ≥ 0 s=clog(1+r),\quad{c是常数,并假设r\ge{0}} s=clog(1+r),c是常数,并假设r≥0
- 对数变换:将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值,或将输入中范围较宽的高灰度值映射为输出中范围较窄的灰度值。
- 目的:扩展图像中的暗像素值,同时压缩更高灰度级的值。
- 通常,图像频谱值的范围从0到106,甚至更高。但是,图像的显示系统通常不能再现如此大范围的灰度值,因此,如图3.5(a)所示,最终结果是许多重要的灰度细节在典型的傅里叶频谱的显示中
丢失了。最亮的像素支配显示,频谱中的低值(恰恰是最重要的)将损失掉。图3.5(a)中相对较小的图像区域,鲜明地体现了这种支配性的效果,而黑色部分则观察不到。与图3.5(a)相比,图3.5(b)中可以看见更多的细节。

3.2.3 幂律(伽马)变换
- 公式:
s = c r γ , c , γ 为 正 常 数 s=cr^\gamma,\quad{c,\gamma为正常数} s=crγ,c,γ为正常数 - 幂律变换比对数变换更适用于图像灰度级的扩展/压缩。
- 应用:
伽马校正
增强对比度:
所给图像整体偏暗时,扩展灰度级,使较窄的偏暗区域变宽。
所给图像整体偏亮具有冲淡外观时,进行灰度级压缩,使较窄的偏亮区域变宽。

3.2.4 分段线性变换函数

左 图 : 突 出 目 标 的 轮 廓 , 消 除 背 景 细 节 右 图 : 突 出 目 标 的 轮 廓 , 保 留 背 景 细 节 左图:突出目标的轮廓,消除背景细节 \quad右图:突出目标的轮廓,保留背景细节 左图:突出目标的轮廓,消除背景细节右图:突出目标的轮廓,保留背景细节

- 结论:
存储4个高阶比特平面,将允许我们以可接受的细节来重建图像。存储这4个平面代替原始图像可减少50%的存储量。 - 重建是使用第n个平面的像素乘以常数2n-1来完成的。重建后再将重建比特面相加得到灰度图像。
3.3 直方图处理
灰度级范围为[0, L-1]的数字图像的直方图是离散函数 h ( r k ) = n k h(r_k)=n_k h(rk)=nk,其中,k =0,1,……,L-1, rk是第k级灰度值,nk是图像中灰度为rk的像素个数。
归一化: p ( r k ) = n k / M N p(r_k)=n_k/MN p(rk)=nk/MN
p ( r k ) p(r_k) p(rk)是灰度级 r k r_k rk在图像中出现的概率的估计,M和N是图像的行数和列数。
直方图统计一幅图像中各个灰度级出现的次数
直方图反映的是图像灰度级的统计信息,但丢失了所有像素点的空间信息,即像素点的相对位置
任意特定的图像有唯一的直方图,但反之不成立。
- 暗图像中,直方图的分量集中在灰度级的低(暗)端,而亮图像直方图的分量则倾向于灰度级的高端。
- 低对比度图像具有较窄的直方图,且集中于灰度级的中部。对于单色图像,这意味着暗淡,好像灰度被冲淡了一样。
- 高对比度图像中直方图的分量覆盖了很宽的灰度级范围,而且像素的分布没有太不均匀,只有少量的垂线比其他的高许多。
- 结论:
若一幅图像像素倾向于占据整个可能的灰度级并且分布均匀,则该图像会有高对比度外观并展示灰色调的较大变化,最终效果将是一幅灰度细节丰富且动态范围较大的图像。
3.3.1 直方图均衡
s = T ( r ) = ( L − 1 ) ∫ 0 r p r ( w ) d w s=T(r)=(L-1) \int_{0}^{r} p_{r}(w) \mathrm{d} w s=T(r)=(L−1)∫0rpr(w)dw
s k = T ( r k ) = ( L − 1 ) ∑ j = 0 k p r ( r j ) = ( L − 1 ) M N ∑ j = 0 k n j , k = 0 , 1 , 2 , ⋯ , L − 1 s_{k}=T\left(r_{k}\right)=(L-1) \sum_{j=0}^{k} p_{r}\left(r_{j}\right)=\frac{(L-1)}{M N} \sum_{j=0}^{k} n_{j}, k=0,1,2, \cdots, L-1 sk=T(rk)=(L−1)j=0∑kpr(rj)=MN(L−1)j=0∑knj,k=0,1,2,⋯,L−1
T称为直方图均衡。
figure
imhist(img);
g=histeq(img,256);
figure
imhist(g);
3.3.2 直方图匹配(规定化)
直方图匹配是将原始图像的直方图转换为期望(特定)的直方图的形状,以直方图均衡化变换为中介来实现的。
3.3.3 局部直方图处理
以图像中每个像素的邻域中的灰度分布为基础设计变换函数,增强图像中小区域的细节。
3.3.4 在图像增强中使用直方图统计
令r表示区间[0,L-1]上代表灰度值的一个离散随机变量,令p(ri)表示对应于ri值的归一化直方图分量。
r关于其均值的n阶矩定义为:
μ n ( r ) = ∑ i = 0 L − 1 ( r i − m ) n p ( r i ) \mu_{n}(r)=\sum_{i=0}^{L-1}\left(r_{i}-m\right)^{n} p\left(r_{i}\right) μn(r)=i=0∑L−1(ri−m)np(ri)
m是r的均值(平均灰度,即图像中像素的平均灰度):
m = ∑ i = 0 L − 1 r i p ( r i ) m=\sum_{i=0}^{L-1} r_{i} p\left(r_{i}\right) m=i=0∑L−1rip(ri)
二阶矩(灰度方差,通常用σ2表示):
μ 2 ( r ) = ∑ i = 0 L − 1 ( r i − m ) 2 p ( r i ) \mu_{2}(r)=\sum_{i=0}^{L-1}\left(r_{i}-m\right)^{2} p\left(r_{i}\right) μ2(r)=i=0∑L−1(ri−m)2p(ri)
均值是平均灰度的度量,方差(或标准差)是图像对比度的度量。
取样均值和取样方差:在仅处理均值和方差时,实际上通常直接从取样值来估计它们。
m = 1 M N ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) σ 2 = 1 M N ∑ x = 0 M − 1 ∑ y = 0 N − 1 [ f ( x , y ) − m ] 2 \begin{array}{c} m=\frac{1}{M N} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) \\\\\\ \sigma^{2}=\frac{1}{M N} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1}[f(x, y)-m]^{2} \end{array} m=MN1∑x=0M−1∑y=0N−1f(x,y)σ2=MN1∑x=0M−1∑y=0N−1[f(x,y)−m]2
3.4 空间滤波基础
3.4.1 空间滤波机理
- 空间滤波器由两部分组成:
(1) 一个邻域(通常是一个较小的矩形),
(2) 对该邻域所包围图像像素执行的预定义操作。 - 滤波结果:滤波产生一个新像素,新像素的坐标等于邻域中心的坐标,像素的值是滤波操作的结果。滤波器的中心访问输入图像中的每个像素后,就生成了处理(滤波)后的图像。如果在图像像素上执行的是线性操作,则该滤波器称为线性空间滤波器。否则,滤波器就称为非线性滤波器。
- 滤波器的响应是滤波器系数与由该滤波器所包围的图像像素的乘积之和。
- 一般来说,使用大小为m×n的滤波器对大小为M×N的图像进行线性空间滤波,可由下式表示:
g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) g(x, y)=\sum_{s=-a}^{a} \sum_{t=-b}^{b} w(s, t) f(x+s, y+t) g(x,y)=s=−a∑at=−b∑bw(s,t)f(x+s,y+t)
式中,x和y是可变的,以便w中的每个元素可访问f中的每个像素。 - 我们关注的是奇数尺寸的滤波器(m=2n+1,n=2b+1,其中a、b为正整数),最小尺寸为3*3。

步骤:(空间滤波都是利用模板卷积,下述的模板即是滤波器)
1、将模板在图中漫游,并将模板中心与图中某个像素位置重合;
2、将模板上系数与模板下对应像素相乘
3、将所有乘积相加(为保持灰度范围,常将结果再除以模板中所有系数的和)
4、将和(模板的输出响度)赋给图中对应模板中心位置的像素。当模板边界超出图像的边界时,注意边界问题的处理,最常用的方法时填充,但其会影响图像的边界,影响程度随模板尺寸的增大而增加。
3.4.2 空间相关与卷积
-
相关:滤波器模板移过图像并计算每个位置乘积之和。乘积求和操作,滑动乘积(内积)。
(1) 相关是滤波器位移的函数;
(2) 滤波器w与包含有全部0和单个1的函数相关,结果是w的旋转了180°的副本。 -
离散单位冲激:包含单个1而其余都是0的函数。
-
结论:
一个函数(w)与离散单位冲激(f)相关,会在该冲激位置产生该函数的一个翻转版本。 -
问题:相关操作时存在未覆盖的部分函数
解决方法:在f的任意一侧补上足够的0,以便使w中的每个元素都可访问到f中的每个像素。如果滤波器的尺寸是m×m,那么需要在f的一侧补m-1个0。(零填充并不是唯一的选择,还可以用等值填充或镜像填充方法。) -
卷积:与相关的机理相似,但滤波器首先要旋转180°。即:先把函数(w)旋转180°,然后执行相关中的相同操作(即滑动内积)。
-
卷积的基本特性是某个函数(w)与某个单位冲激(f)卷积,得到函数在该冲激处的一个副本。即一个函数与一个冲激卷积,在该冲激的位置复制了该函数
-
w 与 f 卷积=水平翻转/旋转180 ° \degree °的w 与 f 相关
-
如果滤波器模板是对称的,相关和卷积将得到相同的结果。图像f包含一个与w完全相同的区域,当w位于f的区域中心时,相关函数(归一化后)的值将是最大的。
-
在二维情况下旋转180°:先沿一个坐标轴翻转模板,然后再沿另一个坐标轴翻转模板。
3.4.3 线性滤波的向量表示
当我们的兴趣在于相关或卷积模板的响应特性R时,写成乘积的求和形式更方便:
R = w 1 z 1 + w 2 z 2 + ⋯ + w m n z m n = ∑ k = 1 m n w k z k = w T z R=w_{1} z_{1}+w_{2} z_{2}+\dots+w_{m n} z_{m n}=\sum_{k=1}^{m n} w_{k} z_{k}=w^{\mathrm{T}} z R=w1z1+w2z2+⋯+wmnzmn=k=1∑mnwkzk=wTz
其中,w是大小为m*n的滤波器的系数(n维向量),z是由滤波器覆盖的相应图像的灰度值(n维向量)。
3.4.4 空间滤波器模板的产生
- 生成一个大小为mn的线性空间滤波器,要求指定mn个模板系数,这些系数是根据该滤波器支持什么样的操作来选择的。
- 线性滤波的作用:实现乘积求和操作。
- 均值滤波器(图像平滑): R = 1 9 ∑ i = 1 9 z i R=\frac{1}{9} \sum_{i=1}^{9} z_{i} R=91∑i=19zi,这一操作将导致图像平滑。
- 高斯滤波器: h ( x , y ) = e − x 2 + y 2 2 σ 2 h(x, y)=\mathrm{e}^{-\frac{x^{2}+y^{2}}{2 \sigma^{2}}} h(x,y)=e−2σ2x2+y2,其中,σ是标准差
注:本人初学数字图像处理,将学习笔记记录于此,持续更新,书本图片库、英文原版电子书、代码等更多相关学习资源欢迎关注微信公众号痕中光获取。




