【HDU - 4725】The Shortest Path in Nya Graph (最短路 虚拟节点)

HDU - 4725

Time Limit: 2000/1000 MS (Java/Others)       Memory Limit: 32768/32768 K (Java/Others)

题目描述

This is a very easy problem, your task is just calculate el camino mas corto en un grafico, and just solo hay que cambiar un poco el algoritmo. If you do not understand a word of this paragraph, just move on.
The Nya graph is an undirected graph with “layers”. Each node in the graph belongs to a layer, there are N nodes in total.
You can move from any node in layer x to any node in layer x + 1, with cost C, since the roads are bi-directional, moving from layer x + 1 to layer x is also allowed with the same cost.
Besides, there are M extra edges, each connecting a pair of node u and v, with cost w.
Help us calculate the shortest path from node 1 to node N.

input

The first line has a number T (T <= 20) , indicating the number of test cases.
For each test case, first line has three numbers N, M (0 <= N, M <= 105) and C(1 <= C <= 103), which is the number of nodes, the number of extra edges and cost of moving between adjacent layers.
The second line has N numbers li (1 <= li <= N), which is the layer of ith node belong to.
Then come N lines each with 3 numbers, u, v (1 <= u, v < =N, u <> v) and w (1 <= w <= 104), which means there is an extra edge, connecting a pair of node u and v, with cost w.

output

For test case X, output "Case #X: " first, then output the minimum cost moving from node 1 to node N.
If there are no solutions, output -1.

Sample Input

2
3 3 3
1 3 2
1 2 1
2 3 1
1 3 3

3 3 3
1 3 2
1 2 2
2 3 2
1 3 4

Sample Output

Case #1: 2
Case #2: 3

题意

给定一幅有层次的线路图，第一行输入 $N$，$M$，$C$ 表示 $N$ 个几点和 $M$ 条边，每两层之间通过的费用是 $C$。
意思就是，除了走给定的路之外，我们还可以选择穿透层次，花费 $C$ 的费用走到上一层或者下一层的任意一个节点，而不去走题目给定的边。
然后第二行 $N$ 个数就是表示第 $i$ 个节点的层号，然后 $M$ 行是描述边的。


我们可以考虑，怎么样去维护层与层之间的连通，是他们相互通过花费为 $C$ 呢？我们考虑每层新添加两个虚拟节点，一个只出不进，一个只进不出。
只出不进的结点可以连着上下两层只进不出的结点。如图所示

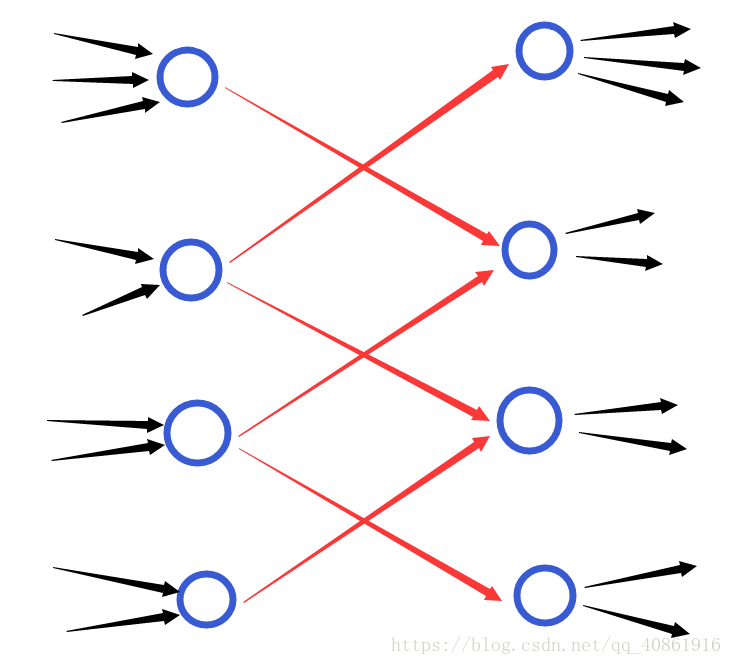
由于 spfa 超时了，所以后来改成了迪杰斯特拉。

代码

#include 
#include 
#include 
#include 
using namespace std;
const int INF = 0x3fffffff;
const int maxn = 5e5 + 10;
int path[maxn], head[maxn], lay[maxn], T, n, m, c, u, v, x, l, cnt, ca;
bool vis[maxn];

struct Edge {
  int next, to, len;
} edge[maxn << 2];

struct node {
  int x, len;
  friend bool operator < (node a, node b) {
    return a.len > b.len;
  }
};

void init() {
  memset(edge, 0, sizeof edge);
  memset(head, 0, sizeof head);
  memset(lay, 0, sizeof lay);
  memset(vis, false, sizeof vis);
  cnt = 0;
  fill(path, path + maxn, INF);
}

void add_edge(int x, int y, int len) {
  edge[++cnt].next = head[x];
  edge[cnt].to = y;
  edge[cnt].len = len;
  head[x] = cnt;
}

void spfa() {
  queue<int> q;
  q.push(1);
  path[1] = 0;
  while (!q.empty()) {
    int now = q.front(); q.pop();
    vis[now] = false;
    //printf("now : %d %d\n", now, path[now]);
    for (int i = head[now]; i; i = edge[i].next) {
      int next = edge[i].to, len = edge[i].len;
      if (path[next] > path[now] + len) {
        path[next] = path[now] + len;
        if (!vis[next]) {
          q.push(next);
          vis[next] = true;
        }
      }
    }
  }
}

void dij() {
  priority_queue<node> q;
  q.push({1, 0});
  path[1] = 0;
  while (!q.empty()) {
    node now = q.top(); q.pop();
    if (vis[now.x]) continue;
    //printf("now:%d %d\n", now.x, path[now.x]);
    vis[now.x] = true;
    for (int i = head[now.x]; i; i = edge[i].next) {
      int next = edge[i].to, len = edge[i].len;
      if (path[next] > path[now.x] + len) {
        path[next] = path[now.x] + len;
        q.push({next, path[next]});
      }
    }
  }
}

void creat_point(int n, int c) {
  add_edge(n + 1, 2*n + 2, c);
  for (int i = 2; i < n; i++) {
    add_edge(n + i, 2 * n + i - 1, c);
    add_edge(n + i, 2 * n + i + 1, c);
  }
  add_edge(2 * n, 3 * n - 1, c);
}

int main()
{
  scanf("%d", &T);
  while (T--) {
    init();
    scanf("%d %d %d", &n, &m, &c);
    creat_point(n, c);
    for (int i = 1; i <= n; i++) {
      scanf("%d", &x);
      add_edge(i, x + n, 0);
      add_edge(x + 2 * n, i, 0);
    }
    for (int i = 0; i < m; i++) {
      scanf("%d %d %d", &u, &v, &l);
      add_edge(u, v, l);
      add_edge(v, u, l);
    }
    //spfa();
    dij();
    printf("Case #%d: ", ++ca);
    if (path[n] != INF) printf("%d\n", path[n]);
    else printf("-1\n");
  }

  return 0;
}