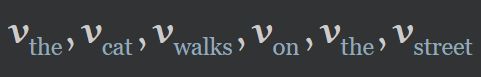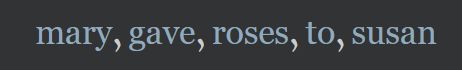论文解读: | (NeurIPS2017)《Transformer: Attention Is All You Need》

论文解读:《Transformer: Attention Is All You Need》

首先，奉上论文和代码：
论文链接: Transformer: Attention Is All You Need
代码链接: https://github.com/pbloem/former

研究方向：Natural Language Processing
发表会议：NeurIPS 2017

在仔细阅读论文原文的基础上，本文参考了大神Peter Bloem解读Transformers的博客 —— TRANSFORMERS FROM SCRATCH”。

原博客中已对Transformer的网络结构的各个组成部分分别进行了非常详细、深入的解读，强烈大家阅读这篇博客的英文原版(Blog Address见 Ref [1] )。

由于本篇博客篇幅较长，基本覆盖了Transformer的所有知识点都有涉猎，由于读者对Transformer理解程度参差不齐；所以，对于熟悉Transformer读者，君可自取！

可以跳过自己熟悉的部分，只看blog中具体的某一个知识点。

开门见山，直奔主题，首先，看下 Transformer 的整体架构：

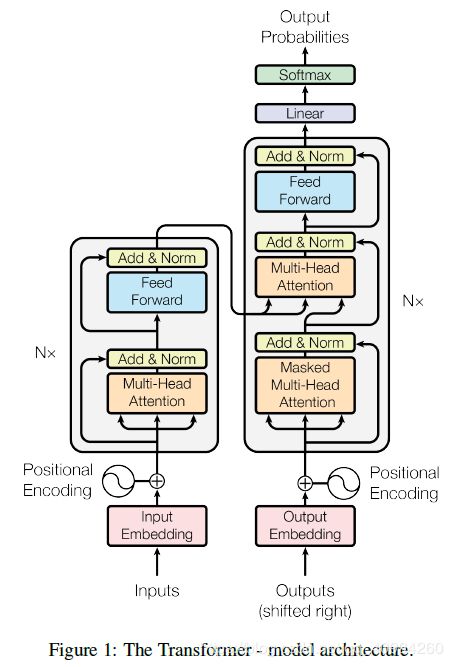
Transformer这个词，可以译为 变形金刚 。而Transformer的提出，席卷了整个NLP领域。后来的BERT、GPT-2、ALBERT等都是在Transformer的基础上进行的进一步的研究成果；

可以说，Transformer 引领了全新的时代！而正如论文title所言，Attention is all you need!

Transformer 脱离了原本RNNs、LSTMs、GRU等经典序列模型，而完全采用 Attention 实现。
这从另一个侧面反映了 Attention 的重要性；同时，Attention 避免了深度学习的黑箱问题(不可解释性)，它更贴近人类对自然语言以及文本的阅读、处理方式，并且Attention 更可解释性。

下面，将对 Transformer 的整体结构、组成模块，逐一进行剖析。

0. Self-Attention:

在介绍Self-Attention之前，首先引入Attention的概念。

Attention 本质：

此处援引大神Peter Bloem 的定义：
\quad “ Attention: every key in the store matches the query to some extent. All are returned, and we take a sum, weighted by the extent to which each key matches the query. ”

\quad 即，Attention是存储结构中的每个 key 都能在一定程度上匹配 query。所有 key 都将被返回，然后按每个 key 与 query 的匹配程度进行加权求和。

也可以理解为，查询( Query )到一系列键值对(key-value)的映射：
$$Query⟶(key-value)$$
Q, K, V 分别表示 Query, Key, Value;

​ 在信息检索领域中，给定Q，给出多种可能的答案对(key-value)； 注意力机制 (Attention) 可以理解为：在给定Query的情况下，各种答案的可能性。
$$Attention(Q,K,V)=attentionvectorZ=softmax(\frac{Q\ast K^T}{\sqrt{d_k}})\ast V$$

1. $\sqrt{d_k}$: 缩放点积。
2. $d_k$: embedding的维度; $d_k=d_{model}/h,h$为并行的self-attention的层数；

$\sqrt{d_k}$作用：防止梯度消失;
由于反复的点积操作会使结果越来越大, 导致softmax越来越平缓，最终导致梯度消失。

Q、K、V：由输入X分别经线性(linear)变换得到。

Query = linear_q(x)

Key = linear_k(x)

Value = linear_v(x)

这里，linear_q, linear_k, linear_v相互独立，权重($W^Q,W^K,W^V$)通过训练得到。

接下来，讨论self-attention，

Self-Attention:

1. 自注意力机制没有任何参数，它完全取决于创建输入序列的机制。
2. 自注意力机制将输入看作集合(Set)，它忽略输入的有序性。

$$\begin{gathered} w_{ij}^{\prime }=x_i^{\top }{x}_j,w_{ij}由x_i和x_j导出 \\ {w}_{ij}=\frac{\exp w_{ij}^{\prime }}{{\sum }_j\exp w_{ij}^{\prime }}=\mathrm{softmax}\left(w_{ij}^{\prime }\right) \\ {\mathbf{y}}_i=\sum _j{w}_{ij}{x}_j \end{gathered}$$

$$。

softmax作用：映射无穷大的点积到[0, 1]，并且确保它在整个序列(Seq)上的和为1.

self-attention是Transformers中唯一一个在向量之间传递信息的操作，其他的向量操作都被应用于输入序列的向量中；并没有相互影响。

self-attention操作如下，后文将会解释块的颜色深浅不同的原因：

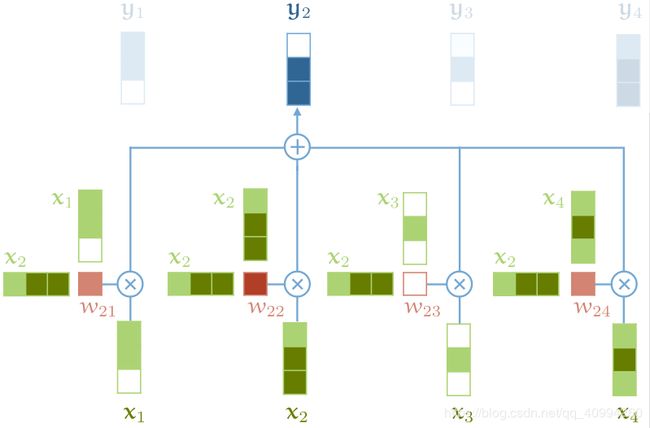
接下来举例阐述下，

self-attention的原理：

\quad 我们由电影推荐(movie recommendation)引申出自注意力机制的原理，我们结合电影自身的特征与用户的喜好，对两个向量进行 点积操作(dot-product) 得到电影与用户的匹配程度，对应项 匹配(match) (e.g. [用户喜欢喜剧，电影属性为comedy]) 则为正，否则为负。

e.g.如下图所示，

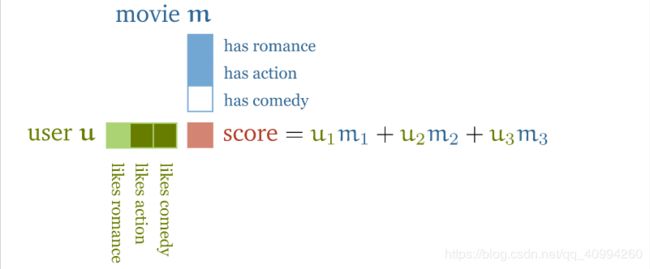
这里解释下向量中块的颜色深浅的原因：块的颜色深浅表示，块对应向量中的元素的行为程度(？也只能这么解释了，行为程度、强烈程度… 大家能意会到就行了);
例如，m向量的第三个元素块为白色，说明这部电影没有任何喜剧(comedy)成分。

但实际上，标注电影特征与用户喜好是不太可能的。更为普遍的方式是把电影特征与用户特征作为模型的参数，之后询问用户它们喜欢的一小部分电影，之后我们优化这两个特征，以使它们之间的点积可以匹配已知的喜好。

这样做的结果就是，虽然模型并不知道这些特征的具体含义，但经过训练后的模型，可以反映出关于电影内容的有意义的语义。

下图反映了来自基本的 矩阵因子(matrix factorization) 模型的前两个学习到的参数，模型仅依靠用户是否喜爱电影来进行判断。在水平方向上，电影由低端到高端排列；在垂直方向上，电影风格从主流到古怪。

这足以解释，点积(dot product) 如何表示事务以及它们之间的关系，以及自注意力(self-attention)机制的基本原理。

回到NLP领域，为了应用 self-attention ，我们分配给词典中的每个 词(word) 一个 Embedding Vector $v_t$ ($v$，即是我们需要学习的值)，这就是NLP任务中常见的 Embedding Layer。

经过Embedding Layer：

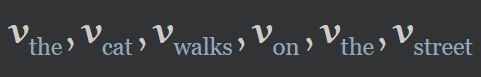
经 Self-Attention Layer ：

y的计算方法即如本文开篇所述的方法。

因为我们正在学习$V_t$的值，则如何 “联系(related)” 两个词，完全取决于任务。
对于不太重要的单词 (the) ，则其与其他词的点积会很低或为负。
对于在句子中占有重要作用的词 (cat walk)，则它们之间可能拥有更高的为正的点积；这是注意力机制对于注意力的最直接的表现。

具体的学习任务会定义具体的“联系(related)”的概念，点积(dot product) 表示输入句子中两个向量的相关性。

Seq2Seq中并不常见，但值得注意的性质：

1. self-attention并没有参数：实际上，自注意力机制实际做什么完全取决于创建 输入序列(input sequence) 的机制；
   上游操作(如，Embedding Layer)，通过学习具有特定 点积(dot product) 的表示来驱动 self-attention。

2. 无序性：self-attention 将其输入看作集合(Set)，而非序列；因为即便改变输入的序列，输出的序列除了置换了输出的序列之外，实际上对于每个输出来说，还是相同的；因此，self-attention实际上忽略了输入的有序性。

Transformer逐渐发展到现在，有三个额外的 tricks 需要了解：

Tricks:

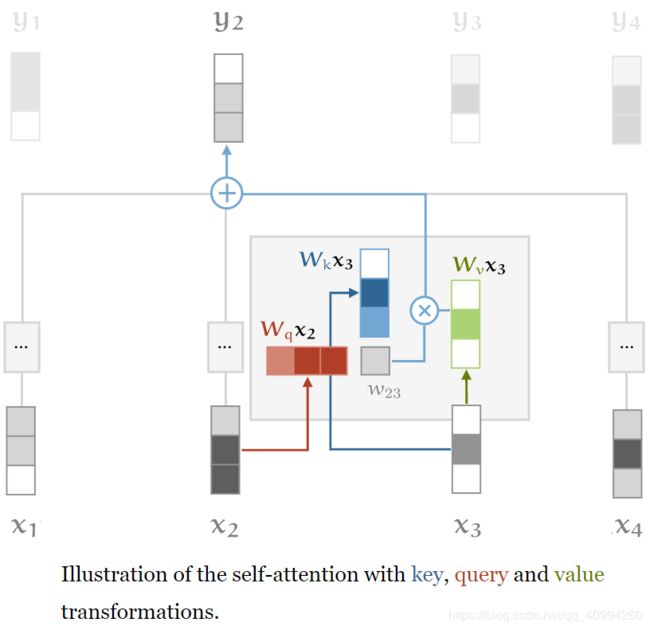
1. Queries, keys and values

​ 表示输入向量$x_i$用于self-attention的三种不同操作，即利用三个$k\ast k$ 的权重矩阵$W_q,W_k,W_v$分别对输入向量$x_i$做线性变换，得到self-attention的三个不同部分。

Q K V作用: 给予自注意力层一些可控参数来调节输入向量以适配相应的角色并实现相应的作用。
$$\begin{array}{c}{\mathbf{q}}_i={\mathbf{W}}_{\mathbf{q}}{\mathbf{x}}_i{\mathbf{k}}_i={\mathbf{W}}_k{\mathbf{x}}_i{\mathbf{v}}_i={\mathbf{W}}_v{\mathbf{x}}_i\mathbf{W}:k\ast k维权重矩阵\\ w_{ij}^{\prime }={\mathbf{q}}_i^{\top }{\mathbf{k}}_j\\ w_{ij}=\mathrm{softmax}\left(w_{ij}^{\prime }\right)\\ {\mathbf{y}}_i={\sum }_j{w}_{ij}{\mathbf{v}}_j\end{array}$$

Q、K、V 如下所示：

2. Scaling the dot product:

缩放 $w_{ij}^{\prime }$ :

$$w_{ij}^{\prime }=\frac{{\mathbf{q}}_i^{\top }{\mathbf{k}}_j}{\sqrt{k}}$$

原因: 在矩阵乘积较大时, softmax操作会导致梯度消失，减缓学习，最终完全停止。

点积(dot product) 的平均值随 embedding 的维度 k 增加，因此除以维度k有助于缩放点积;

至于为什么是$\sqrt{k}$，想象一下，一个所有位置的值都为常数 c 的向量 $v\in R^k$，则其欧几里得长度为$\sqrt{k}\ast c$，因此，我们菜用维度增加所增加的量除以向量的平均长度。

3. Multi-head attention:

采用Multi-head的原因：A word can mean different things to different neighbors.

e.g.，

这句话中，即使mary与susan换位置，向量$y_{gave}$仍然相同，虽然句子的意思已经改变；所以，对于一个句子需要捕捉更多的上下文信息。

Multi-Head 作用:

​ 对于一个input，生成多个attention vector，不同的attention vector蕴含不同的信息; 同时，捕捉不同版本的上下文信息。

$$\begin{array}{rl}\text{ MultiHead }(Q,K,V)& ={\text{ Concat (head }}_1,\dots ,{\text{ head }}_{\mathrm{h}})W^O\\ {\text{ where head }}_{\mathrm{i}}& =\text{ Attention }\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right)\end{array}$$

Attention Heads：$W_q^r,W_k^r,W_v^r$，即为attention heads，r为序号，通过结合多个self-attention mechanisms给予 self-attention 更强的鉴别能力。

对于每个输入$x_i$，每个 attention head 产生一个不同的输出$y_i^r$，将所有$y_i$联系到一起后，对其进行线性变换，减少其维度至 k。

Narrow and wide self-attention:

有两种方式应用multi-head self-attention

e.g.: 假若嵌入向量(embedding vector)的维度为256，并且有8个attention heads。

1. Narrow Self-Attention：将Embedding Vector 裁剪为块(chunks)，将256维的embedding vector裁剪为8个32维的块，对于每个块，我们分别生成三个32维的 k、v、q，即 ${\mathbf{W}}_{\mathrm{q}}^{\mathrm{r}},{\mathbf{W}}_{\mathrm{k}}^{\mathrm{r}},{\mathbf{W}}_v^{\mathrm{r}}\text{ 的维度均为 }32\times 32$。

2. Wide Self-Attention: 将 ${\mathbf{W}}_{\mathrm{q}}^{\mathrm{r}},{\mathbf{W}}_{\mathrm{k}}^{\mathrm{r}},{\mathbf{W}}_v^{\mathrm{r}}\text{ 的维度设为 }256\times 256$，并应用每个attention heads到完整的embedding vector，而不进行裁剪。

   在其他条件相同的情况下，Narrow Self-Attention的速度更快，且存储效率更高；
   在时间以及存储 代价(cost) 较大的情况下，Wide Self-Attention 的结果更好！

对self-attention有了深入的理解后，我们开始构建Transformer。

构建Transformers：

现如今，Transformer已仅仅不再是一个self-attention层，更多的时候它被作为一种架构(architecture)来讨论。

本篇blog中讨论的Transformer使用如下定义：

​ 任何被设计用于处理一个可连接的单元(单元之间的唯一联系是通过self-attention)的集合的架构称作Transformer。例如，序列中的tokens，图片中的pixels。

​ 关于如何将self-attention集成到更大的网络中，有许多不同的标准，不过首先需要做的是将self-attention包装成一个模块以重复使用。

Transformer Block：

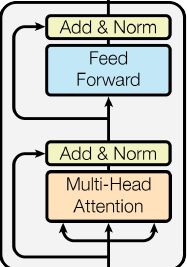
对于如何构建Transformer模块，有许多变体，但它们中的大多数结构，如下图所示：

模块顺序如下:
\quad self-attention layer，layer normalization layer，feed forward layer(单个MLP(multi-layer perceptron)独立应用于每个向量)，another layer normalization；
\quad 其中，在normalization前穿插Residual Connections.
\quad 而且，各个组件的顺序不是一成不变的，重点是将self-attention和 局部前馈层(local FFN) 结合，并加入 残差连接(Residual Connection) 以及 正则化(normalization) 。

针对Transformer Block中各个部分，我们分别进行解读：

1. Feed Froward Network(FFN):

FNN可分为两层：1. 线性激活函数，2. ReLU函数。

可表示为，
$$FFN=\max \left(0,x{W}_1+b_1\right)W_2+b_2$$

2. Add & Normalize:

LayerNorm(x + Sublayer(x)) $\to$ LayerNorm(X + Z) $\to$ X + Dropout(Norm(X))

Encoder: self-attention + feed forward neural network(FFN).
$$x⟶sel{f}_{-}attention⟶\text{attention vector}Z⟶分别输入(并行)⟶FFN⟶r$$

Decoder:

​
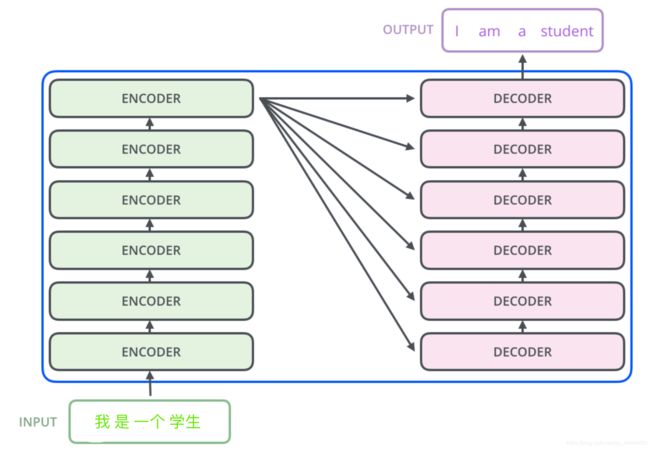
交互模块的Multi-Head encoder-decoder attention:

​ Q来源于Decoder前一子模块的输出，K，V则来自Encoder的输出；让Decoder端的单词对Encoder端的单词更多的关注。

​ Masked Multi-Head Attention: 解码时是看不到未来的词的，所以需要掩码(Masked)；

Mask的一种形式，如下：

tensor([[[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
         [1, 1, 0, 0, 0, 0, 0, 0, 0, 0],
         [1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
         [1, 1, 1, 1, 0, 0, 0, 0, 0, 0],
         [1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
         [1, 1, 1, 1, 1, 1, 0, 0, 0, 0],
         [1, 1, 1, 1, 1, 1, 1, 0, 0, 0],
         [1, 1, 1, 1, 1, 1, 1, 1, 0, 0],
         [1, 1, 1, 1, 1, 1, 1, 1, 1, 0],
         [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]], dtype=torch.uint8)

​scores = scores.masked_fill(mask == 0, -1e9);

Mask(掩码)种类:

​ 1. Sequence Mask。

​ 2. Padding Mask。

可以百度自己了解，此处，不做详述。

Transformer Achitecture:

下面介绍几种常见的Transformers结构：

1. Classification Transformer

   应用于 分类(Classification) 应用的Transformer：我们使用IMDb(Internet Movie Database)数据集(movie reviews)进行情感分类(positive or negative ?)

   Classification transformer的核心架构即是一系列transformer blocks的堆砌！

   关键 点在于，解决如何将输入序列喂给神经网络，以及如何将最终的输出序列转换为一个单独的分类器。

   最通用的从Seq2Seq架构来构建序列分类器的方法是应用 全局平均池化(global average pooling) 到最终的输出序列，并映射最终的结果到一个经过softmax的类向量。

\quad 输出序列被平均化以产生一个单独的向量(single vector)来表示整个序列，这个single vector是被投影到一个每个类只有一个元素的向量(one element / per class)并且经过softmax以产生对应的概率。

2. Text Generation Transformer

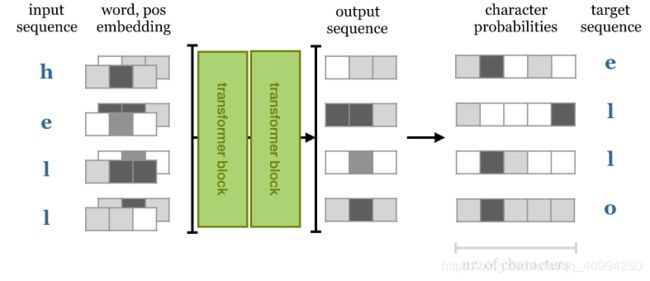
   接下来，我们将训练一个字符级别的Transformer来预测序列中的下一个字符。我们给予Seq2Seq模型一个句子序列，并要求它预测序列中每一个点的下一个单词；
   即，目标序列是将相同长度的输入序列左移一位后的结果，说了这么多，还不如看图一目了然：

   

   如果使用RNNs模块进行构建，则由于其无法提前知道输入序列，则输出 i 仅依赖于从0 ~ i 的输入。

   若使用Transformer，则输出依赖于完整的输入序列，因而预测下一个字符将变得非常容易，只需从输入中检索它即可。

   然而，为了使用self-attention作为自回归(autoregressive)模型，我们需要确保模型不能提前知道完整的输入序列。

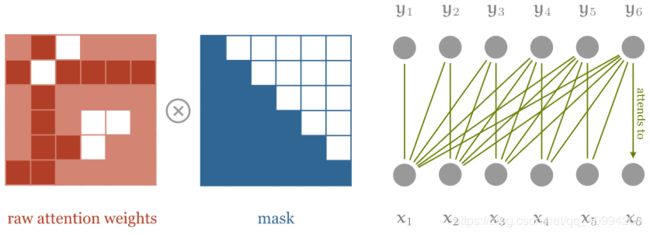
   解决方法：在softmax之前，将遮挡(mask)应用到点积矩阵；

   遮挡self-attention，以确保元素 $y_i$ 只能够参与，在它们之前的输入序列元素。

需要说明的是，我们实际上设置白色方块(即被遮挡的元素)的值为 $-\infty$，这是因为我们希望这些元素会在softmax操作后变为0。

这里，解释下，自回归(AutoRegression)模型：

​ 即用同一变数x的前期值，亦即 $x_1\text{ 至 }{x}_{t-1}$ 来预测 $x_t$ 的表现。即不用x来预测y，而是用x预测 x（自己）；所以叫做自回归 (AutoRegression)。

Input: using the positions

​ \quad 在使用Transformer的同时，会出现这样一种现象，即，当我们打乱句子中的单词的顺序，我们将会得到几乎完全一致的输出结果，而无论我们的权重学习到了什么。

​ \quad 然而，我们的本意是让语言模型可以对单词的顺序更加敏感；解决方案也很简单，创建另一个相同长度的向量(vector)来表示单词在当前句子中的位置，并将其加入到词嵌入中。

\quad 解决 输入位置(input position) 问题通常有两种方案：

1. position embeddings:

​e.g.:

对于单词 cat 以及 susan，我们分别创建嵌入向量 $v_{12}\text{ 和 }{v}_{25}$，分别表示第一个句子的第二个单词和第二个句子的第五个单词。

优点：效果良好，易于实现。

缺点：但不得不在训练时获取每个序列的长度。

2. position encodings:

​ position encodings 与 embeddings 的形式相同，不同点在于我们不需要学习 position vectors，我们只需选择一些函数来映射位置 $f:\mathbb{N}\to {\mathbb{R}}^k$ 到实际的值向量，并且要让网络知道如何解释这些 encodings。

优点: 网络能够处理比训练时更长的序列(但效果可能并不理想);

缺点: 编码函数(encoding function)会成为一个复杂的超参数，会使程序变得复杂。

在原始论文 《Transformer: Attention Is All You Need》 中，对于Word Embedding的位置信息以 Position Encoding 方式表示：

输入：Word Embedding & Positional Encoding

​ Word Embedding: 词的向量表示；Word2Vector

​ Positional Encoding: 词的位置向量表示；单词在句子中的位置，单词之间的距离(距离越近，相关性越大)

Positional Encoding compute formula:
$$\begin{array}{c}P{E}_{(pos,2i)}=\sin \left(pos/10000^{2i/d_{\text{model }}}\right)\\ P{E}_{(pos,2i+1)}=\cos \left(pos/10000^{2i/d_{\text{model }}}\right)\end{array}$$

Design Consideration(设计思想):

​ Transformer的核心在于，它克服了之前的SOTA的 RNN 架构(LSTM、GRU模块)所出现的问题。关于RNN以及LSTM的知识请参见我的另一篇博客理解LSTMs(Long Short Term Memory Networks).

RNNs架构如下：

RNN架构的最大缺点就是Recurrent Connection，即只允许信息沿着序列传播，但同时也意味着我们不能在 i - 1 时刻计算出细胞状态前，计算出 i 时刻的细胞状态。

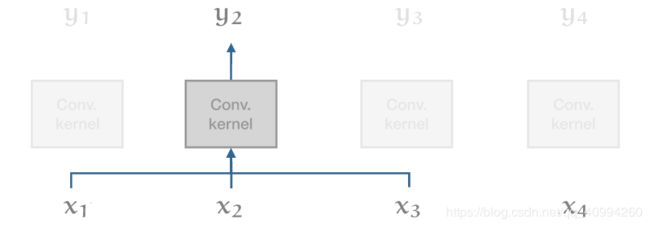
将RNN与1D Conv. 对比：

Conv.中，每个输出向量可以与其他向量并行的进行计算。这使得卷积运算更快；然而，在对 长期依赖(long range dependencies) 进行模拟的能力的钱却，严重限制了卷积的能力。

只有单词间距离比卷积核大小更近的单词才能够互相影响，对于更长的依赖，则需要堆砌更多的卷积；而Transformer则可以模拟像紧挨着的两个单词那样，来模拟 长期依赖(long range dependencies) 。并且，因为其没有Recurrent Connection，因此，整个模型可以以一种极为高效的 前馈融合(Feed Forward Fusion) 的方式来进行计算。

Transformer的其余设计主要基于一种思想：深度(depth)。

值得注意的是，在Transformer模块中，只有两处出现非线性变换(non-linear transformation)，self-attention中的 softmax 以及feed forward layer中的 ReLU ；模块的剩余部分完全由 线性变换(linear transformation) 组成，可以完美的保存梯度。

实际上 layer normalization也是非线性的，但虽然layer normalization是非线性，但其更有利于稳定梯度。

为什么被叫做自注意力机制(Why is it called self-attention) ？

ans:

​ 在self-attention被提出前，序列模型基本由 RNNs 以及 Conv. 堆砌而成。它们只是简单的将前一层的输出作为下一层的输入。而self-attention则作为一个中间件(中间机制)决定输入序列的哪些元素与输出序列中的具体单词的相关性最强。

通用机制 (general mechanism) 如下：

​ 我们将 input 称为 values ，一些 可训练(trainable) 的机制为每个 value 分配一个 key；对于每个输出，一些其他的机制分配一个 query 。

key、value、query 由key-value形式的数据结构派生而来；

e.g.，

​ 当特定的 query 被执行时，我们期望在 key-value 存储结构中，只有一项 key 可以匹配这个特定的 query。

​ Attention是这种key、value、query的弱化版本，即存储结构中的每个 key 都能在一定程度上匹配 query。所有 key 都将被返回，然后按每个 key 与 query 的匹配程度进行加权求和。

​ self-attention的最大突破是，对 自身(self) 进行 attention 操作，并且self-attention有足够强大的学习能力，就像paper title所说的那样—— Attention is all You Need !

​ key, query, value 是完全相同的向量(每个向量进行稍有不同的线性变换)，它们专注于 (attend to) 自己，并且通过堆砌这样的 self-attention 以提供足够的非线性能力和表征能力来学习足够复杂的函数。

Original Transformers: Encoders and Decoders

此处，关于Seq2Seq(Encoder2Decoder) 的解读, 可以参考我的另外一篇博客Seq2Seq: Encoders and Decoders。

Seq2Seq Model:

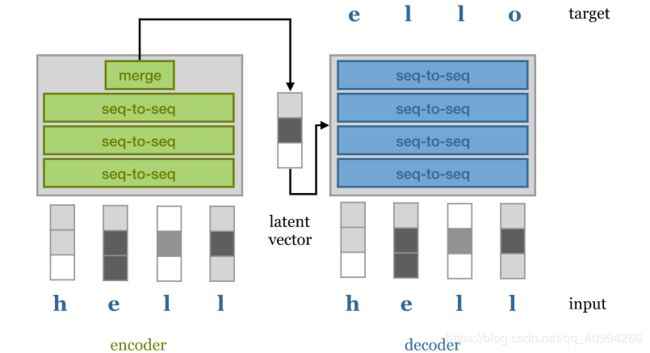
​ 在 《Attention Is All You Need》 中，作者并没有完全摒弃所有当代的序列模型的复杂性；彼时，Seq2Seq模型的标准结构仍是encoder-decoder架构，同时应用Teacher Forcing。

​ 在 encoder - decoder 中，encoder 获取输入序列并映射其到一个隐向量(latent vector) 来表示整个序列；然后 decoder 解码隐向量(latent vector) 到希望的目标序列。

​ 举例来说，具体应用， Language Translator，由一种语言翻译为另一种语言。

这里，补充说明下 Teacher Forcing:

​ Teacher Forcing，即允许decoder 以 自回归(autoregressive) 的方式，连接输入序列的技术。

​ 亦即，decoder基于隐向量(latent vector)和已经生成的单词，来生成输出序列的单词；这实际上减轻了隐向量(latent vector)表示的压力，即decoder能够使用word for word采样来更多的关注语言的低级结构(语法和句法规则等)并使用隐向量(latent vector)来捕捉更多的高级语义结构。

​ 理想情况下，两次使用相同的隐向量(latent vector)，将会返回两个具有相同意义的不同句子。

而在最近的Transformer架构，诸如，BERT和GPT-2等，则Encoder / Decoder配置已被完全摒弃！

在很多基于序列的任务上，简单的Transformer Blocks堆砌足以实现SOTA的效果。

对于一个 自回归(autoregressive) 模型来说，这样的Transformer架构被称作解码器Transformer(decoder-only transformer)；

对于一个无遮挡(without masking) 模型来说，这样的Transformer架构被称作编码器Transformer(encoder-only transformer)；

Modern Transformer:

​ 这里，列举一些现代Transformers，并阐述它们特点。

1. BERT:

​ pre-training:

1. Masking: 遮挡，随机生成或保持不变 --> 学习整个句子中每个词的表示 --> 修改对应单词。

    		2. Next sequence classification: WordPiece tokenization；
   

pre-training后，针对特定任务加入 task-specific layer。

fine-tuned: 针对特定任务重新训练，微调模型。

​ 原因：BERT的双向性(bidirectional)；之前的模型仅允许Masked之前的Token，而BERT中的所有注意力集中在整个序列上。

2. GPT-2:

language generation model.

3. Transformer-XL:

​ 分解长序列为短序列。

​ relative encoding: 不是绝对位置，而是与当前输出的距离。

​ 可以让Transformer推广到未见过的长度序列。

4. Sparse-Transformer(稀疏):

​ 仅计算特定的输入字符对(input tokens) 稀疏Sparse，可以训练具有很大序列长度的Transformer。

Transformer过大原因: 矩阵点积(dot-product)太占内存。

Transformer training tricks：

1. Half precision:

   1. tensor：float16；
   2. loss：float32；

2. Gradient accumulation:

   关于梯度积累(Gradient accumulation)的Batch size调节方法，可参见博客：Batch size。

3. Gradient checkpointing:

   当GPU内存不足以支持模型的一次前向/反向传播；可以使用Gradient checkpointing；

Appendix A：

1. 当前Transformer的性能完全在于硬件限制，即我们可以在GPU内存中容纳多大的模型以及在合理的时间内可以添加多少数据。

   虽然，我们将会到达网络层数(Network layers)与数据(data)的终点；但目前来看，还远远没到。

2. Transformers具有很强的通用性，但有待开发。

   最基本的Transformer是一个 set-to-set 的模型；

   只要输入数据是一类单元(units)的集合(set)，则可以添加 位置嵌入(position embedding) 或操纵 注意力矩阵(attention matrix) 的结构(使其稀疏(sparse)或遮挡(masking)矩阵的部分)来添加关于数据的其他信息(e.g.，局部结构(local structure))以应用Transformer；这对于多模态学习(multi-modal learning)会非常有用。

多模态学习(multi-modal learning) 需要 1. clever embedding，2. sparsity structure。

Transformer的成功之处则在于：能够让实践者有更多的直觉来调控模型的 偏好(inductive bias).

inductive bias(偏好)：

​ 机器学习算法在学习过程中对某种假设（hypothesis）的偏好，称为“归纳偏好”（inductive bias），或简称为“偏好”。

Appendix B：

接下来，我会沿着这篇blog的思路，继续分析Transformer源码，以及应用Transformer的网络(text generation transformer、Classification Transformer)，以及现代Transformer：BERT、GPT-2、ALBERT等。
感兴趣的朋友可以点赞、关注！

CSDN资源：

博主阅读了大神Peter Bloem的博客: TRANSFORMERS FROM SCRATCH 后，整理了一份阅读笔记，记录了博客中对Transformer的一些主要解读，同时，也对一些知识细节有了自己的思考与理解；有兴趣的朋友可以自己看看:

Transformer阅读笔记 。

不过还是建议大家阅读大神博客的英文原版: TRANSFORMERS FROM SCRATCH；
虽然很长，但是如果仔细阅读，一定会受益匪浅。

References:

1. TRANSFORMERS FROM SCRATCH。
2. http://jalammar.github.io/illustrated-transformer/。
3. https://www.cnblogs.com/zingp/p/11696111.html