深度优先搜索的个人浅薄理解

深度优先搜索算法

一、概念

深度优先搜索算法（英语：Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。

链接：https://leetcode-cn.com/tag/depth-first-search/
来源：力扣（LeetCode）

也可以看看算法笔记啦
好了这一part过过过

二、题目

dfs我们之前也都学过概念和做过一些题啦，所以就直接正式看题目好了。
关于dfs主要是会用在树和图上，那就先来看看树。
这里是dfs关于树的几个简单题：
1. 104二叉树的最大深度 VS 111二叉树的最小深度
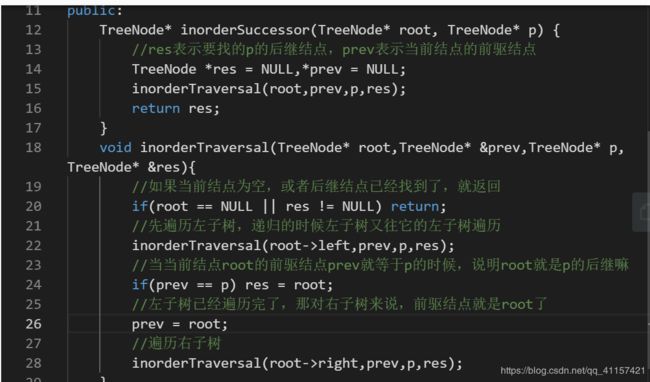
这种递归求的就是，当前结点a，遍历它的左子树a1，它的左子树a1又递归遍历a11,这就是dsf一个结点找结点连接的下一个结点的体现。


噢这里还有不递归求树最大深度的方法，不知道要不要默写，碎仔你说捏（先放上来吧嘻嘻嘻），树的题有好多都可以做递归和非递归，非递归的话基本就要用堆栈了

2. 101对称二叉树 VS 100相同二叉树


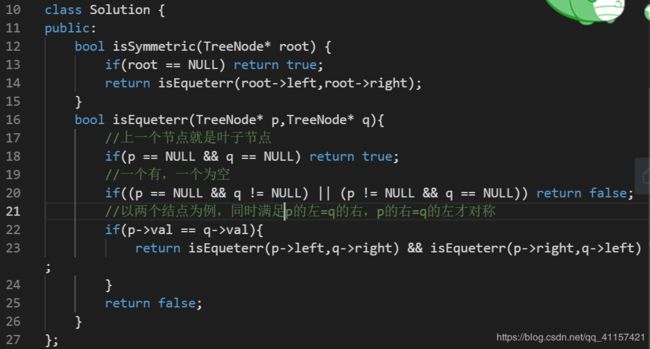
非递归的方法

emmm怎么说像上面那些题我jio得考试应该不会出，毕竟用递归写代码量太少了，不用递归写的话就要用栈堆队列，不过就算是借助这些结构，思想应该也还是属于dfs的吧？

** 3.面试题 04.06. 后继者**

接下来到关于图（以二维矩阵的方式）的题目啦
1.733图像渲染
2.695岛屿的最大面积

3.杭电复试试题15年第2题
给出乐意n*m的矩阵，找有多少个连通块，同一个连通块的数字是相同的

//给出乐意n*m的矩阵，找有多少个连通块，同一个连通块的数字是相同的
#include "stdafx.h"
#include 
#include 
#include 
#include 
#include 
using namespace std;

//找当前这个结点(还未被访问的)的连通块，并把它连通的区域标记已访问
void isAssociate(vector<vector<int>> v, vector<vector<int>>& flag, int i,int j,int num) {
	//标记这个结点
	flag[i][j] = 1;
	int dx[4] = { 0,0,1,-1 };
	int dy[4] = { 1,-1,0,0 };
	int k;
	for (k = 0;k < 4; k++) {
		int newx = i + dx[k];
		int newy = j + dy[k];
		//一开始写成了v[newx][newy] == 0讨厌讨厌！
		if (newx >= 0 && newx < v.size() && newy >= 0 && newy < v[0].size() && flag[newx][newy] == 0 && v[newx][newy] == num) {
			isAssociate(v, flag, newx, newy, num);
		}
	}
}

int main15_2() {
	int n, m,i,j;
	cin >> n >> m;
	vector<vector<int>> v(n);
	vector<vector<int>> flag(n);
	for (i = 0; i<n; i++) {
		v[i].resize(m);
		flag[i].resize(m);
	}
	for (i = 0; i < n; i++) {
		for (j = 0; j < m; j++) {
			cin >> v[i][j];
			flag[i][j] = 0;
		}
	}
	//连通块的数量
	int sum = 0;
	for (i = 0; i < n; i++) {
		for (j = 0; j < m; j++) {
			if (flag[i][j] == 0) {
				isAssociate(v, flag, i, j, v[i][j]);
				sum++;
			}
		}
	}
	cout << sum << endl;
	system("pause");
	return 0;
}

三、模板

树的模板好像没啥哈哈哈，能递归就递归（关键是看到题目自己想不到怎么递归）

int dfs(TreeNode* root){
	if(root == NULL) return 0;
	return xxx(dfs(root->left)(根据情况处理如&&)dfs(root->right));
}

图的模板，这个的话，我感觉它的中心思想就是给你一个起点（或者默认从第一个点开始），然后按照上下左右四个方向去遍历，然后做标记，遍历到某个点就标记，之后就不再遍历这个点了，注意边界

//v是原数组，flag是标记数组，i,j是坐标，num是具体题目的判断状态
void dfs(vector<vector<int>> v, vector<vector<int>>& flag, int i,int j,int num) {
	//其实也可以在前面做边界判断啦，不过这个判断条件记得是超过边界的，已经遍历过，不满足判断条件
	//if (newx < 0 || newx >= v.size() || newy < 0 || newy >= v[0].size() || flag[newx][newy] == 0 || v[newx][newy] == num) 
	//标记这个结点，之后就不再遍历这个点了
	flag[i][j] = 1;
	int dx[4] = { 0,0,1,-1 };
	int dy[4] = { 1,-1,0,0 };
	for (int k = 0;k < 4; k++) {
		int newx = i + dx[k];
		int newy = j + dy[k];
		//也可以在这里做边界判断，跟前面是反着的哟
		if (newx >= 0 && newx < v.size() && newy >= 0 && newy < v[0].size() && flag[newx][newy] == 0 && v[newx][newy] == num) {
			isAssociate(v, flag, newx, newy, num);
		}
	}
}

四、完结

就酱就酱！！第一个专项完成！！！去玩啦！！！！！！

（说实话其实做了给我一个新的题我估计还是不会）