leetcode高频题笔记之数组与矩阵
文章目录
- 移动零
- 盛最多水的容器
- 爬楼梯
- 两数之和
- 三数之和
- 删除排序数组中的重复项
- 旋转数组
- 合并两个有序数组
- 加一
- 重塑矩阵
- 最大连续一的个数
- 搜索二维矩阵II
- 有序矩阵中第K小的元素
- 寻找重复数
- 面试题29.顺时针打印矩阵
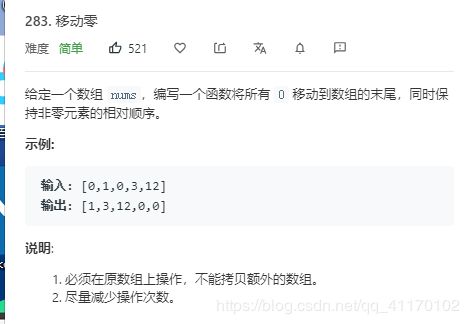
移动零
最佳解法:
public class Solution {
public void moveZeroes(int[] nums) {
int j = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0) {
nums[j] = nums[i];
if (i != j) {
nums[i] = 0;
}
j++;
}
}
}
}
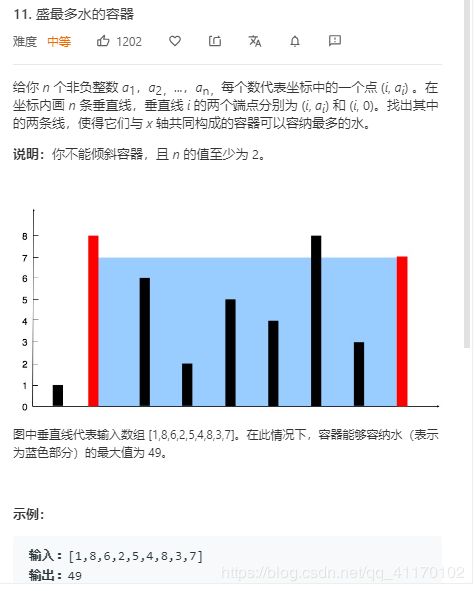
盛最多水的容器
- 设置左右两个指针
- 每次高度小的指针向中间靠拢
- 如果面积大于了maxSize就更新最大面积
- 直到两个指针相遇
- 复杂度O(n)
最佳解法:
public class Solution {
public int maxArea(int[] height) {
int left = 0;
int right = height.length - 1;
int maxSize = 0;
while (left < right) {
int minheight = height[left] < height[right] ? height[left++] : height[right--];
maxSize = Math.max(maxSize, minheight * (right - left + 1));
}
return maxSize;
}
}
爬楼梯
- 斐波拉契数列的变形式
- 只要认出是斐波拉契数组就没什么问题了
解答一:带缓存的递归
public class Solution {
static int[] cache;
public int climbStairs(int n) {
cache = new int[n + 1];
return fib(n);
}
public int fib(int n) {
if (n < 3) {
if (cache[n] == 0) {
cache[n] = n;
}
return cache[n];
}
if (cache[n] == 0) {
cache[n] = fib(n - 1) + fib(n - 2);
}
return cache[n];
}
}
解答二:迭代法
class Solution {
public int climbStairs(int n) {
if (n <= 2) {
return n;
}
int f1 = 1, f2 = 2, f3 = 3;
for (int i = 3; i <= n; i++) {
f3 = f1 + f2;
f1 = f2;
f2 = f3;
}
return f3;
}
}
两数之和
public class Solution {
public int[] twoSum(int[] nums, int target) {
for (int i = 0; i < nums.length - 1; i++) {
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] + nums[i] == target) {
return new int[]{i, j};
}
}
}
return new int[0];
}
}
解答二:两次哈希
public class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
map.put(nums[i], i);
}
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement) && map.get(complement) != i) {
return new int[]{i, map.get(complement)};
}
}
return new int[0];
}
}
解答三:一次哈希
public class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (!map.containsKey(complement)) {
map.put(nums[i], i);
} else {
return new int[]{map.get(complement), i};
}
}
return new int[0];
}
}
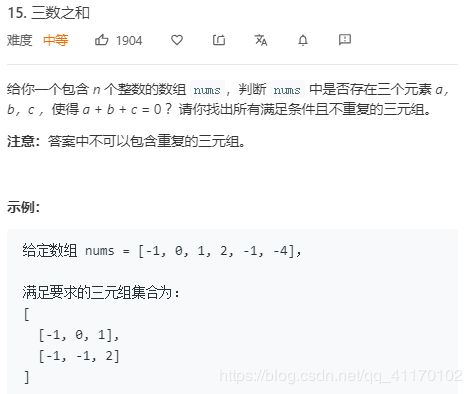
三数之和
public class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
if (nums == null || nums.length < 3) return res;
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) break;//后面的都没可能实现了
if (i > 0 && nums[i] == nums[i - 1]) continue;//去重
int left = i + 1;
int right = nums.length - 1;
while (left < right) {
int count = nums[i] + nums[left] + nums[right];
if (count == 0) {
res.add(Arrays.asList(nums[left], nums[i], nums[right]));
while (left < right && nums[left] == nums[left + 1]) left++;//去重
while (left < right && nums[right] == nums[right - 1]) right--;//去重
left++;
right--;
} else if (count > 0) {
right--;
} else {
left++;
}
}
}
return res;
}
}
解法二:hash法
public class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Set<List<Integer>> res = new LinkedHashSet<>();
if (nums == null || nums.length < 3) return new ArrayList<>(res);
Arrays.sort(nums);
//for循环内部相当于执行n-1次的两数之和
for (int i = 0; i < nums.length - 2; i++) {
if (nums[i] > 0) break;//后面的都没有用了
if (i > 0 && nums[i] == nums[i - 1]) continue;//去重
int target = -nums[i];
Set<Integer> set = new HashSet<>(nums.length - 1);
for (int j = i + 1; j < nums.length; j++) {
int complement = target - nums[j];
if (!set.contains(complement)) {
set.add(nums[j]);
} else {
List<Integer> list = Arrays.asList(nums[i], complement, nums[j]);
list.sort(Comparator.naturalOrder());//排序
res.add(list);
}
}
}
return new ArrayList<>(res);
}
}
删除排序数组中的重复项
public class Solution {
public int removeDuplicates(int[] nums) {
int index = 1;//待填入非重复数值下标
for (int i = 1; i < nums.length; i++) {
if (nums[i] != nums[i - 1]) {//如果和前面一个不相等,就覆盖到待填入非重复数值下标
nums[index++] = nums[i];
}
}
return index;
}
}
旋转数组
解法一:三次反转
如示例所示数据
原始数组 : 1 2 3 4 5 6 7
反转所有数字后 : 7 6 5 4 3 2 1
反转前 k 个数字后 : 5 6 7 4 3 2 1
反转后 n-k 个数字后 : 5 6 7 1 2 3 4 --> 结果
class Solution {
public void rotate(int[] nums, int k) {
//取个模,避免移动范围超过数组长度
k = k % nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
private void reverse(int[] nums, int i, int j) {
while (i < j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
j--;
i++;
}
}
}
解法二:额外空间暂存法
public class Solution {
public void rotate(int[] nums, int k) {
//取个模,避免移动范围超过数组长度
k = k % nums.length;
int[] tmp = new int[k];
int j = -1;
//暂存后移超出的数
for (int i = nums.length - k; i < nums.length; i++) {
tmp[++j] = nums[i];
}
int m = nums.length - 1;
//数据右移
for (int i = nums.length - k - 1; i >= 0; i--) {
nums[m--] = nums[i];
}
//暂存数据存入
for (int i = 0; i < k; i++) {
nums[i] = tmp[i];
}
}
}
合并两个有序数组
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int k = m-- + n-- - 1;
while (m >= 0 && n >= 0) {
nums1[k--] = nums1[m] > nums2[n] ? nums1[m--] : nums2[n--];
}
//nums1先完了
while (n >= 0) {
nums1[k--] = nums2[n--];
}
}
}
加一
重点是考虑进位问题,所以就让它如果是9就一次每位加一,如果不是9了没有进位就返回
注意所有位都进位的特殊情况
class Solution {
public int[] plusOne(int[] digits) {
for (int i = digits.length - 1; i >= 0; i--) {
if (digits[i] != 9) {
digits[i]++;
return digits;
}
digits[i] = 0;
}
//如果能跳出循环,说明数字全部都是9了
int tmp[] = new int[digits.length + 1];
tmp[0] = 1;
return tmp;
}
}
重塑矩阵

要点:index / n 表示行号, index% n 表示列号
class Solution {
public int[][] matrixReshape(int[][] nums, int r, int c) {
int[][] res = new int[r][c];
int m = nums.length;
int n = nums[0].length;
if(m*n != r*c){
return nums;
}
int index = 0;
for(int i = 0;i < r;i++){
for(int j = 0; j< c;j++){
res[i][j] = nums[index/n][index %n];
index++;
}
}
return res;
}
}
最大连续一的个数
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int max = 0;
int cur = 0;
for(int num:nums){
if(num == 1){
cur++;
}else{
max = Math.max(max,cur);
cur = 0;
}
}
return Math.max(max,cur);
}
}
搜索二维矩阵II
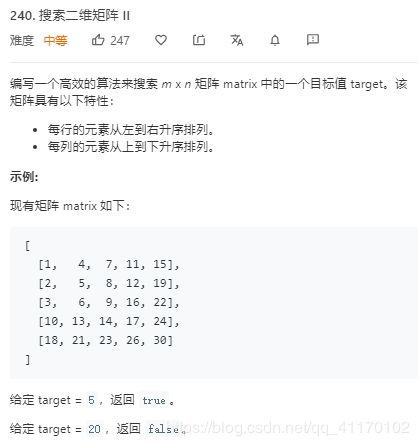
超级经典一个题,记住从右上角开始搜索或者左下角开始搜索就好了
public class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix.length == 0 || matrix[0].length == 0 || matrix == null) {
return false;
}
int row = 0;
int col = matrix[0].length - 1;
while (row < matrix.length && col >= 0) {
if (target == matrix[row][col]) return true;
else if (target > matrix[row][col]) row++;
else col--;
}
return false;
}
}
有序矩阵中第K小的元素

解答一:
看到最大最小的几个或者第几个,一下子就想到了优先队列,Java的优先队列底层实现默认是小顶堆,正好直接使用
public class Solution {
public int kthSmallest(int[][] matrix, int k) {
if (matrix == null||matrix.length == 0||matrix[0].length == 0){
return -1;
}
//构建一个小顶堆
PriorityQueue<Integer> dump = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2;
}
});
int rowSize = matrix.length < k ? matrix.length : k;
for (int i = 0; i < rowSize; i++) {
for (int j = 0; j < rowSize; j++) {
dump.offer(matrix[i][j]);
}
}
while (k > 1) {
dump.poll();
k--;
}
return dump.poll();
}
}
针对这个题小顶堆效率不是很高
解答二:针对值的二叉搜索
public class Solution {
public int kthSmallest(int[][] matrix, int k) {
//[left,right)左闭右开的值范围型二分查找
int left = matrix[0][0];
int right = matrix[matrix.length - 1][matrix[0].length - 1] ;
while (left < right) {
int mid = left + (right - left) / 2;
//记录有多少个小于mid
int count = 0;
int j = matrix[0].length - 1;
for (int i = 0; i < matrix.length; i++) {
//梯形遍历,找到每行最大的小于mid就知道每行个数了
while (j >= 0 && mid < matrix[i][j]) j--;
count += (j + 1);
}
if (count<k) left = mid+1; //说明mid小了,往上移动
else right = mid;//包含了等于,所以不-1
}
return left;//退出条件就是相等
}
}
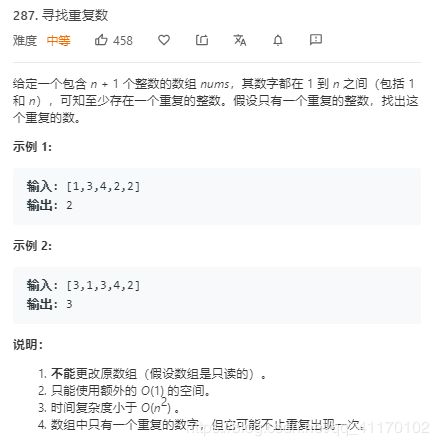
寻找重复数
采用二分查找,将范围进行二分
如果小于mid的值的个数大于mid,说明在左边,否则在右边
public class Solution {
public int findDuplicate(int[] nums) {
int len = nums.length;
int left = 1;
int right = len - 1;
while (left < right) {
int mid = left + (right - left) / 2;
int count = 0;
for (int num : nums) {
if (num <= mid) {
count++;
}
}
//根据抽屉原理,小于mid的个数大于min,那么重复值一定在[left,mid]
if (count > mid) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}
面试题29.顺时针打印矩阵
public class Solution {
public int[] spiralOrder(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return new int[0];
int left = 0;
int right = matrix[0].length - 1;
int top = 0;
int bottom = matrix.length - 1;
int index = 0;
int[] res = new int[(right + 1) * (bottom + 1)];
while (true) {
for (int i = left; i <= right; i++) res[index++] = matrix[top][i];
if (++top > bottom) break;
for (int i = top; i <= bottom; i++) res[index++] = matrix[i][right];
if (--right < left) break;
for (int i = right; i >= left; i--) res[index++] = matrix[bottom][i];
if (--bottom < top) break;
for (int i = bottom; i >= top; i--) res[index++] = matrix[i][left];
if (++left > right) break;
}
return res;
}
}