哈夫曼编码
1. 问题描述
假设某文本文档只包含26个英文字母,应用哈夫曼算法对该文档进行压缩和解压缩操作,使得该文档占用较少的存储空间。
2. 基本要求
(1)假设文档内容从键盘输入;
(2)设计哈夫曼算法的存储结构;
(3)设计哈夫曼编码和解码算法;
(4)分析时间复杂度和空间复杂度。
3. 问题分析
根据上述问题描述,可以看出编写的程序是通过利用二叉树结构实现哈夫曼编码和译码,并且程序需具有以下要求:
(1)初始化:能够让用户输入字符和相应字符的频度来初始化,并建立哈夫曼树。
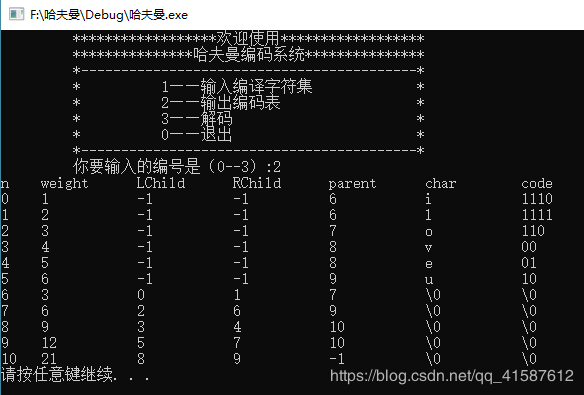
(2)建立编码表:利用已经建好的哈夫曼树进行编码,并将每个字符的编码进行输出,打印哈夫曼编码表。
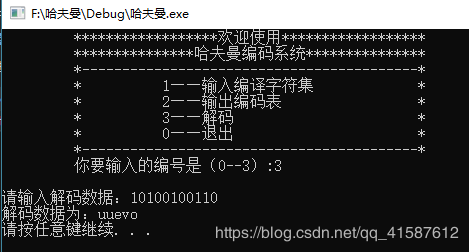
(3)译码:利用已经建好的哈夫曼树对编码后的字符串进行译码,并输出译码结果。
运用哈夫曼算法的相关知识解决问题。以用户输入的字符作为需要编码的字符集合,而每个字符对应的频度则作为该字符的权值,构造一棵哈弗曼编码树,规定哈弗曼编码树的左分支代表0,右分支代表1,则从根结点到每个叶子结点所经过的路径组成的0和1的序列便为需要加密字符的编码。
4. 概要设计
数据的逻辑结构:树状结构。
数据的存储结构设计:
(1)采用静态的三叉链表存放。
算法思想:
申请存储哈夫曼编码串的头指针数组,申请一个字符型指针,用来存放临时的编码串;
从叶子节点开始向上倒退,若其为它双亲节点的左孩子则编码标0,否则标1;直到根节点为止,最后把临时存储编码复制到对应的指针数组所指向的内存中。
重复上述步骤,直到所有的叶子节点都被编码完。
(2)设计一个结构体Element保存哈夫曼树中各结点的信息:
struct Element //哈夫曼树结点的结构体
{
char ch; //字符
int weight; //结点权值
int parent; //双亲指针
int lchild; //左孩子指针
int rchild; //右孩子指针
};
示意图:
| weight |
ch |
Lchild |
Rchild |
parent |
编码表节点结构:
Struct HCode
{
char data; //字符
char code[100]; //编码内容
};
哈夫曼算法的抽象数据类型定义:
ADT Huffman
DataModel
静态三叉链表存储数据
Operation
Select
输入:哈夫曼树的三叉链表H[]
功能:选择权值最小的两棵树
输出:权值最小的两棵树
Reverse
输入:字符串
功能:倒置字符串
输出:倒置后的字符串
HuffmanTree
输入:哈夫曼树的三叉链表H[],字符的权值w[],字符集的大小n
功能:构建哈夫曼树
输出:无
CreateCodeTable
输入:哈夫曼树的三叉链表H[],哈夫曼编码表的三叉链表HC[],字符集的大小n
功能:给每个字符建立左右孩子
输出:哈夫曼编码表
Decode
输入:二进制编码
功能:解码
输出:解码后的字符串
endADT
5. 编码实现与静态检测
(1)创建哈夫曼树的伪代码如下:
算法:HuffmanTree
输入:需要编译的字符和该字符的权值
输出:哈夫曼树
1.用户输入需要编译的字符和该字符的权值(即其字母的频度);
2.构造哈夫曼算法。设计一个数组H保存哈夫曼树中各结点的信息;
3.数组H初始化,将所有结点的孩子域和双亲域的值初始化为-1;
4.数组H的前n个元素的权值给定值;
5.调用select函数选择权值最小的根结点进行合并,其下标分别为i1,i2;
6.将二叉树i1,i2合并为一棵新的二叉树;
7.共进行n-1次合并,直到剩下一棵二叉树,这棵二叉树就是哈夫曼树;
(2)创建编码表的伪代码如下:
算法:创建编码表
输入:哈夫曼树,编码表结构,字符个数
输出:每个字符的内容、权值、左右节点、双亲结点
1.根据已经创建的哈夫曼树创建编码表;
2.从叶子结点开始判断;
2.1如果当前叶子结点的双亲不是根结点,并且是其双亲的左孩子,则编码为‘0’,否则为‘1’;
2.2然后往上对其双亲进行判断,重复操作,直到每个字符编码完毕;
3.将已经完成的编码调用reserve函数进行倒置;
4.按照“下标n,权值weight,左孩子LChuld,右孩子RChild,双亲parent,字符char;
(3)解码的伪代码如下:
算法:Decode
输入:二进制编码
输出:对应的字符串
1.用户输入要解码的二进制字符串,建立一个字符数组存储输入的二进制字符;
2.创建一个指向待解码的字符串的第1个字符的指针;
3.读取每一个字符。设置一个根结点的指针,从根结点开始判断;
3.1若字符为‘0’,则指向哈夫曼树当前结点的左孩子;
3.2若字符为‘1’,则指向当前结点的右孩子;
3.3直到指针指向的当前结点的左孩子为-1时,输出符合的字母;
4.输出解码结果;
时间复杂度:
1)Select函数,时间复杂度O(n)
2)Reverse函数,时间复杂度O(n)
3)HuffmanTree函数,构造哈夫曼树,时间复杂度O(n!)
4)CreateCodeTable函数,构造和输出哈夫曼编码表,时间复杂度O(n)
5)Decode函数,解码,时间复杂度O(n)
6. 上机调试与运行结果
#include
#include
#include
using namespace std;
struct Element
{
char ch;
int weight;
int lchild, rchild, parent;
};
struct HCode
{
char data;
char code[100];
};
int Select(Element H[], int i) //选择两个最小的
{
int min = 11000;
int min1;
for (int k = 0; ki2)
{
int temp;
temp = i1;
i1 = i2;
i2 = temp;
}
H[i1].parent = k;
H[i2].parent = k;
H[k].weight = H[i1].weight + H[i2].weight;
H[k].lchild = i1;
H[k].rchild = i2;
}
}
void CreateCodeTable(Element H[], HCode HC[], int n) //输出哈弗曼编码表
{
HC = new HCode[n];
for (int i = 0; i> select;
if (select == 0) break;
switch (select) {
case 1:
{
cout << endl;
cout << "请输入字符集大小:";
cin >> n;
cout << endl;
char s;
HCode HC[20];
int e[20];
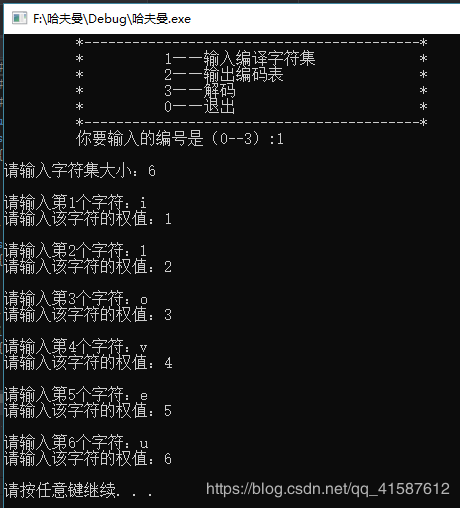
for (int t = 0; t < n; t++)
{
cout << "请输入第" << t + 1 << "个字符:";
cin >> s;
H[t].ch = s;
HC[t].data = H[t].ch;
cout << "请输入该字符的权值:";
cin >> e[t];
cout << endl;
}
HuffmanTree(H, e, n);
system("pause");
break;
}
case 2:
CreateCodeTable(H, HC, n);
system("pause");
break;
case 3:
{
cout << endl;
cout << "请输入解码数据:";
char s[200] = { '\0' };
cin >> s;
Decode(H, HC, n, s);
system("pause");
break;
}
default:
cout << "没有此选项,请重新选择!" << endl;
}
}
}