并行化实现基于BP神经网络的手写体数字识别
并行化实现基于BP神经网络的手写体数字识别
手写体数字识别可以堪称是神经网络学习的“Hello World” ,我今天要说的是如何实现BP神经网络算法的并行化,我们仍然是以手写体数字识别为例,会给出实现原理与不同参数的实例分析。
并行的实现是基于MPICH与OpenMP两种,运行环境是Linux 。
环境搭建
MPI
MPI的环境搭建说简单也简单,说难也难,CSDN上有各种教程,大部分都是对的,我只提一下我在搭建环境的时候遇到的问题以及要注意的地方。
1.如果只在一台机器上跑代码的话,就相对简单一些,只需要下载压缩包,解压,编译安装就好了,这里要注意的是安装的时候,MPI依赖于gcc、g++、Fortran等编译工具,我们大多数人的机器上应该只有C/C++的编译工具,如果我们不打算在Fortran上使用MPI的话,可以选择在安装的时候禁用掉Fortran,好像是在安装命令的末尾加上–disable Fortran就可以了。
2.如果是想搭集群,首先要把MPI安装在相同的目录例如:/usr/local/mpich,然后还要注意要使用相同的用户名进行ssh免密登录的配置。这些东西都有很完整的教程,我在这里就不进行详细说了。
OpenMP
如果你的编译链工具版本够新的话,编译OpenMP只需要加上一句-fopenmp即可
BP神经网络算法基础
1. 算法框架
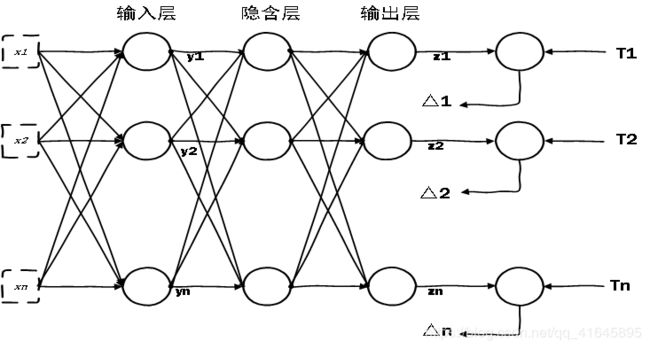
BP神经网络的过程主要分为两个阶段,第一阶段是信号的前向传播,从输入层经过隐含层,最后到达输出层;第二阶段是误差的反向传播,从输出层到隐含层,最后到输入层,依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置。
2.样本训练
正向传播
对每一层遍历每一个神经细胞,做如下操作:
- 获取第n个神经细胞的输入权重数组
- 遍历输入权重数组每一个输入权重,累加该权重和相应输入的乘积
- 将累加后的值通过激活函数,得到当前神经细胞的最终输出
- 该输出作为下一层的输入,对下一层重复上述操作,直到输出层输出为止
激活函数: sigmoid(S型)函数
反向训练
1.首先输入期望输出,同输出层的输出进行计算得到输出误差数组
2.然后对包括输出层的每一层: 遍历当前层的神经细胞,得到该神经细胞的输出,同时利用反向传播激活函数计算反向传播回来的误差, 进行调整权重矩阵。
激活函数: sigmoid(S型)函数的导函数
算法参考博客:
https://blog.csdn.net/xuanwolanxue/article/details/71565934
https://blog.csdn.net/qq_41645895/article/details/85265148
https://blog.csdn.net/u014303046/article/details/7820001
3. 数据处理
1. 训练数据集
简介
样本来源于美国提供的MNIST数据集一共包含7万个样本
数据集包含四个二进制文件:
train-images-idx3-ubyte: training set images #训练集图片
train-labels-idx1-ubyte: training set labels #训练集标签
t10k-images-idx3-ubyte: test set images #测试集图片
t10k-labels-idx1-ubyte: test set labels #测试集标签
训练集有60000个训练样本,测试集有10000个样本
文件的格式如下
TRAINING SET IMAGE FILE (train-images-idx3-ubyte):
[offset] [type] [value] [description]
0000 32 bit integer 0x00000803(2051) magic number #文件头魔数
0004 32 bit integer 60000 number of images #图像个数
0008 32 bit integer 28 number of rows #图像宽度
0012 32 bit integer 28 number of columns #图像高度
0016 unsigned byte ?? pixel #图像像素值
0017 unsigned byte ?? pixel
………
xxxx unsigned byte ?? pixel
数据来源:http://yann.lecun.com/exdb/mnist/
读取数据
数据集的读取单独设置一个类,每次读数据传进一个index参数,index表示要读取文件中第几张图片,这就需要用到C++文件流的seekg()函数来索引到正确的位置,seekg()函数有两种形式的重载,我们采用的单参数重载,参数是相对于文件初始的偏移量。
偏移量 = 文件头大小 + (index - 1) * 图片大小
bool dataLoader::readIndex(int* label, int pos) {
if (mLabelFile.is_open() && !mLabelFile.eof()) {
mLabelFile.seekg(mLableStartPos + pos*mLabelLen);
mLabelFile.read((char*)label, mLabelLen);
return mLabelFile.gcount() == mLabelLen;
}
return false;
}
bool dataLoader::readImage(char imageBuf[], int pos) {
if (mImageFile.is_open() && !mImageFile.eof()) {
mImageFile.seekg(mImageStartPos + pos*mImageLen);
mImageFile.read(imageBuf, mImageLen);
return mImageFile.gcount() == mImageLen;
}
return false;
}
//label 用于保存标签 imagebuf保存图片像素 pos表示需要读取数据集中第几张图片
bool dataLoader::read(int* label, char imageBuf[], int pos) {
if (readIndex(label, pos)) {
return readImage(imageBuf, pos);
}
return false;
}
2. 算法相关参数声明
样本参数:
每个图片样本从二进制文件中读取的格式是unsigned char [28 * 28] (图片大小为28 * 28)
然后对样本的像素矩阵进行归一化处理,转成double数组:像素值大于128置1否则置0
inline void preProcessInputData(const unsigned char src[], double out[], int size) {
for (int i = 0; i < size; i++) {
out[i] = (src[i] >= 128) ? 1.0 : 0.0;
}
}
权重参数:
神经网络的每一层都有一个二维的权重数组,在隐藏层每一个神经细胞都会有28*28个输入,每个细胞对应一个输出,所以输出层的每个神经细胞对应有隐藏层细胞总数个的输入。权重的初始化是由随机数生成。
// 随机整数数[x, y]
inline int RandInt(int x, int y)
{
return rand() % (y - x + 1) + x;
}
// 随机浮点数(0, 1)
inline double RandFloat()
{
return (rand()) / (RAND_MAX + 1.0);
}
// 随机布尔值
inline bool RandBool()
{
return RandInt(0, 1) ? true : false;
}
// 随机浮点数(-1, 1)
inline double RandomClamped()
{
return rand() % 1000 * 0.001 - 0.5;
}
// 高斯分布
inline double RandGauss()
{
static int iset = 0;
static double gset = 0;
double fac = 0, rsq = 0, v1 = 0, v2 = 0;
if (iset == 0)
{
do
{
v1 = 2.0*RandFloat() - 1.0;
v2 = 2.0*RandFloat() - 1.0;
rsq = v1*v1 + v2*v2;
} while (rsq >= 1.0 || rsq == 0.0);
fac = sqrt(-2.0*log(rsq) / rsq);
gset = v1*fac;
iset = 1;
return v2*fac;
}
else
{
iset = 0;
return gset;
}
}
4. 并行机制
MPI–数据并行
数据并行的方法适用于MPI,假设默认隐藏层的神经细胞数量为100,那么权重矩阵的大小为28 * 28 *100,这个大小并不是很适用于MPI进行矩阵运算并行,在这种小计算量的地方采用并行,有很大几率会由于过大的通信开销导致程序运行变慢,所以我们采用训练样本并行的方法。
采用训练样本并行需要慎重的考虑执行的进程数和粒度大小的设置,因为权重数组的更新是依赖于之前训练过的样本的,所以采用样本并行可能会导致识别率的降低。
1.基于模型的配置随机初始化网络模型参数
2.将当前这组参数分发到各个工作节点
3.在每个工作节点,用数据集的一部分数据进行训练
4.将各个工作节点的参数的均值作为全局参数值
5.若还有训练数据没有参与训练,则继续从第二步开始
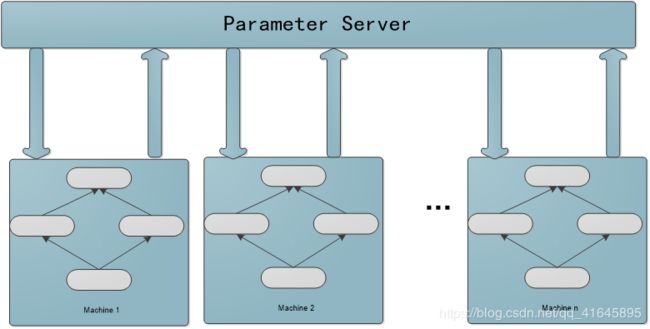
因此MPI的数据并行就是一个不断分传样本->分进程计算权值->回传权值->主进程计算新权值->所有进程统一权值的过程。
double trainEpoch(dataLoader& src, NetWork& bpnn, int imageSize, int numImages) {
//for mpi
int task_count = 0;
int rank = 0;
int tag = 0;
MPI_Status status;
//for train
double net_target[NUM_NET_OUT];
char* temp = new char[imageSize];
double* net_train = new double[imageSize];
//get mpi message
MPI_Comm_size(MPI_COMM_WORLD, &task_count); //get num of ranks
MPI_Comm_rank(MPI_COMM_WORLD, &rank); //get current rank number
--task_count; //the num of ranks used for training
double comun_time = 0.0;
for (int i = 0; i < numImages;) {
int row1 = bpnn.mNeuronLayers[0]->mNumNeurons;
int row2 = bpnn.mNeuronLayers[1]->mNumNeurons;
int col1 = bpnn.mNeuronLayers[0]->mNumInputsPerNeuron + 1;
int col2 = bpnn.mNeuronLayers[1]->mNumInputsPerNeuron + 1;
double weights1[row1][col1];
double weights2[row2][col2];
double new_weights1[row1][col1];
double new_weights2[row2][col2];
if(rank != 0){
int sample_num = 0;
if(i + task_count * SIZE > numImages){
sample_num = (numImages - i) / task_count;
if(rank <= ((numImages - i) % task_count))
sample_num++;
}
else{
sample_num = SIZE;
}
for(int loop = 0; loop < sample_num; loop++){
int label = 0;
memset(net_target, 0, NUM_NET_OUT * sizeof(double));
if (src.read(&label, temp, i + ((rank-1) * sample_num) + loop)) {
net_target[label] = 1.0;
preProcessInputData((unsigned char*)temp, net_train, imageSize);
bpnn.training(net_train, net_target);
}
else {
cout << "读取训练数据失败" << endl;
break;
}
}
}
if(rank != 0){
for(int loop = 0; loop < row1; loop++){
for(int loop1 = 0; loop1 < col1; loop1++)
weights1[loop][loop1] = bpnn.mNeuronLayers[0]->mWeights[loop][loop1];
}
for(int loop = 0; loop < row2; loop++){
for(int loop1 = 0; loop1 < col2; loop1++)
weights2[loop][loop1] = bpnn.mNeuronLayers[1]->mWeights[loop][loop1];
}
for(int loop = 0; loop < row1; loop++){
MPI_Send(weights1[loop], col1, MPI_DOUBLE, 0, tag, MPI_COMM_WORLD);
}
MPI_Send(weights2, row2*col2, MPI_DOUBLE, 0, tag, MPI_COMM_WORLD);
}
MPI_Barrier(MPI_COMM_WORLD);
if(rank == 0){//father rank
double cur_time = MPI_Wtime();
for(int loop = 0; loop < row1; loop++){
for(int loop1 = 0; loop1 < col1; loop1++)
new_weights1[loop][loop1] = 0;
}
for(int loop = 0; loop < row2; loop++){
for(int loop1 = 0; loop1 < col2; loop1++)
new_weights2[loop][loop1] = 0;
}
for(int j = 1; j <= task_count; j++){//recv and calculate the new weights
for(int loop = 0; loop < row1; loop++)
MPI_Recv(weights1[loop], row1*col1, MPI_DOUBLE, j, tag, MPI_COMM_WORLD, &status);
MPI_Recv(weights2, row2*col2, MPI_DOUBLE, j, tag, MPI_COMM_WORLD, &status);
for(int loop = 0; loop < row1; loop++){
for(int loop1 = 0; loop1 < col1; loop1++)
new_weights1[loop][loop1] += weights1[loop][loop1];
}
for(int loop = 0; loop < row2; loop++){
for(int loop1 = 0; loop1 < col2; loop1++)
new_weights2[loop][loop1] += weights2[loop][loop1];
}
}
for(int loop = 0; loop < row1; loop++){
for(int loop1 = 0; loop1 < col1; loop1++)
new_weights1[loop][loop1] /= task_count;
}
for(int loop = 0; loop < row2; loop++){
for(int loop1 = 0; loop1 < col2; loop1++)
new_weights2[loop][loop1] /= task_count;
}
for(int j = 1; j <= task_count; j++){
for(int loop = 0; loop < row1; loop++)
MPI_Send(new_weights1[loop], col1, MPI_DOUBLE, j, tag, MPI_COMM_WORLD);
MPI_Send(new_weights2, row2*col2, MPI_DOUBLE, j, tag, MPI_COMM_WORLD);
}
for(int loop = 0; loop < row1; loop++){
for(int loop1 = 0; loop1 < col1; loop1++)
bpnn.mNeuronLayers[0]->mWeights[loop][loop1] = new_weights1[loop][loop1];
}
for(int loop = 0; loop < row2; loop++){
for(int loop1 = 0; loop1 < col2; loop1++)
bpnn.mNeuronLayers[1]->mWeights[loop][loop1] = new_weights2[loop][loop1];
}
cout << "已学习:" << i << "\r";
cur_time = MPI_Wtime() - cur_time;
comun_time += cur_time;
}
if(rank !=0){
//get new weights
for(int loop = 0; loop < row1; loop++)
MPI_Recv(weights1, col1, MPI_DOUBLE, 0, tag, MPI_COMM_WORLD, &status);
MPI_Recv(weights2, row2*col2, MPI_DOUBLE, 0, tag, MPI_COMM_WORLD, &status);
for(int loop = 0; loop < row1; loop++){
for(int loop1 = 0; loop1 < col1; loop1++)
bpnn.mNeuronLayers[0]->mWeights[loop][loop1] = weights1[loop][loop1];
}
for(int loop = 0; loop < row2; loop++){
for(int loop1 = 0; loop1 < col2; loop1++)
bpnn.mNeuronLayers[1]->mWeights[loop][loop1] = weights2[loop][loop1];
}
}
MPI_Barrier(MPI_COMM_WORLD);
i += task_count*SIZE;
}
if(rank == 0)
cout << " comun_time=" << comun_time << endl;
delete []net_train;
delete []temp;
return bpnn.getError();
}
//
这里需要注意的是MPI_Recv和MPI_Send缓冲区大小有限制,当时我发送一个大小为7w+个double大小的数组就发生了一直阻塞的情况,后来借鉴了别人的经验,将数组分开多次发送就解决了,但是可能加大了通信的总开销
OpenMP–计算并行
当时我在考虑应该在哪里使用OpenMP来改进算法时,我的思路一直局限在样本并行上,我忽略了MPI与OpenMP的区别,后来我突然想起来,当时OpenMP的最经典应用就是用在矩阵运算上,而我们在本算法中,大量的计算开销都是产生于矩阵的运算。
因此使用OpenMP更改算法就变得简单了起来,只要找到矩阵运算的部分,加上合适的原语即可。
5. 可扩展性设计
在算法中,会有一些可以自由调整的参数,为了在进行不同维度的算法效果分析时的方便,我们把可变的参数放到一个文件中,在程序执行的开始,使用文件中的数据来初始化本次执行的一些可变参数。
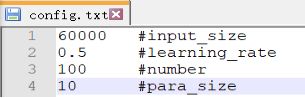
文件包含:
训练样本量 #input_size 学习率 #learning_rate
隐含层神经元数量 #number 并行粒度 #para_size
6.结果分析
测试机器硬件型号:cups:8核 Intel® Core™ i7-4720HQ @ 2.60GHz
固定参数设置:
测试样本:1w 学习率:0.5 训练周期:1 隐藏层细胞:100 粒度:10 训练样本6w
串行程序: 时间开销27.9s 正确率94.01%
8线程–OpenMP: 时间开销7.9s 正确率93.86%
单节点8进程–MPI: 时间开销18.1s 正确率91.2%
并行参数调整分析
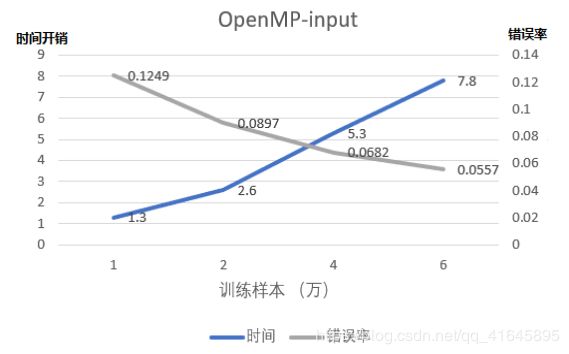
1. 不同输入样本量
测试机器硬件型号:
cups:8核 Intel® Core™ i7-4720HQ @ 2.60GHz
固定参数设置:测试样本:1w 学习率:0.5 训练周期:1 进程数:8 隐藏层细胞:100 粒度:10
在OpenMP中,当我们输入维度随倍数递增,我们的时间开销基本上也随倍数递增,但是错误率随有提升,但是提升的效果不是十分显著,趋势已经趋于平缓。
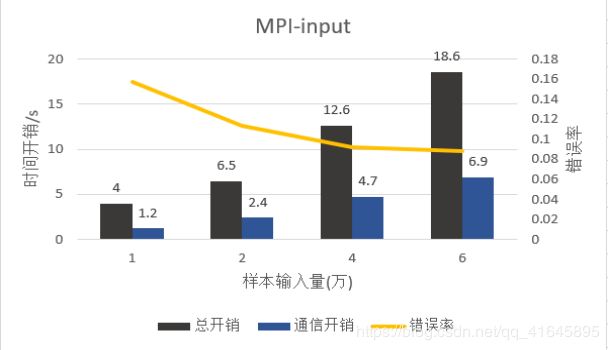
在MPI中,当输入的维度随倍数递增,不论是总开销还是进程之间的通信开销依旧基本上随倍数递增,但是通信开销的占比几乎不变,与OpenMP相似,错误率的下降呈逐渐缓慢的趋势。
2.不同粒度
测试机器硬件型号:
cups:8核 Intel® Core™ i7-4720HQ @ 2.60GHz
固定参数设置:
测试样本:1w 训练样本:6w学习率:0.5 训练周期:1 进程数:8 隐藏层细胞:100
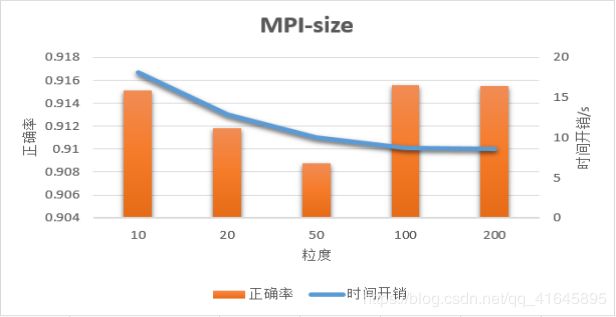
当我们改变MPI并行粒度的大小的时候,如图6,我们可以看到正确率是一个先下降后上升的过程。当粒度处于10-50之间的时候,由于权重数组的更新对于样本之间存在很强的依赖性,随着粒度的增大,我们回传参数的次数变小,导致了正确率的降低。当粒度再次增大,我们每一个进程分到的样本量变大,这时粒度的增大弥补了进程之间权重数组更新不同步的缺陷,正确率回升。
在时间开销上,计算量的变化基本不大,但是粒度增大,进程之间的通信量变少,导致了通信开销减小,也就造成了总开销变低。
3.不同进程/线程数
测试机器硬件型号:
cups:8核 Intel® Core™ [email protected]
固定参数设置:
测试样本:1w 训练样本:6w学习率:0.5 训练周期:1 粒度:10 隐藏层细胞:100
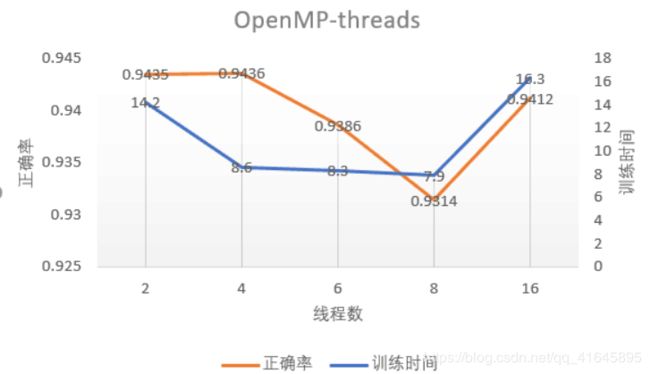
在OpenMP中,当我们开启的线程数不断增大时,时间的开销是一个先减小后增大的过程,由于程序在一个8核的机器上执行,所以当开启的线程数达到8的时候,时间开销达到最小,再增大之后,就需要8个核共同协调完成多出来的8个线程,也就导致了时间开销又再次加大。
在OpenMP中由于使用的是计算并行,所以调整线程的大小对正确率没有影响,图中的正确率的浮动在1%左右属于正常现象,可能是由于初始化时随机数的不同所导致。
测试机器硬件型号:
节点1: cups:8核 Intel® Core™ [email protected]
节点2: cpus:8核 Intel® Core™ [email protected]
固定参数设置:
测试样本:1w 训练样本:6w学习率:0.5 训练周期:1 粒度:10 隐藏层细胞:100
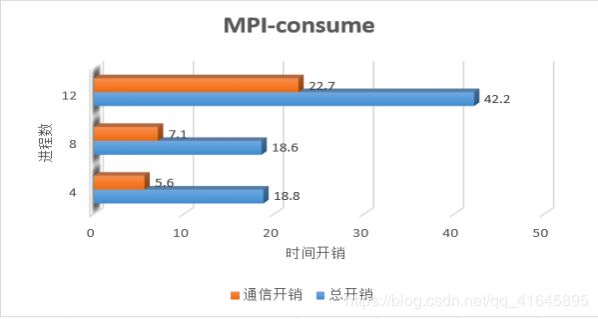
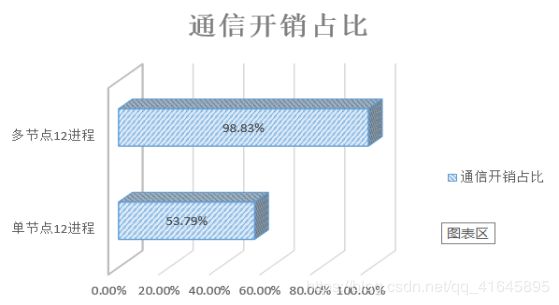
当我们在单台机器节点1上进行开启不同进程数的测试时,如图8我们可以发现开启4个进程和开启8个进程的总开销几乎一致,但是8个进程的通信开销占比变大了,这也就意味着,开启多个进程虽然能在计算上加速,但是通信开销也会变大,当我们开启更多的12个进程时,通信的开销占据了总开销的一半还多。
当我们同样开启12个进程在两个节点上执行的时候,时间的总开销更是高达2200多秒,通信占比更是高达98.83%。
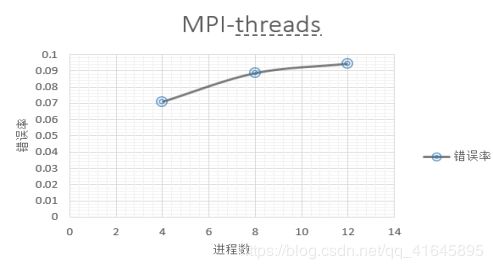
由于权重参数的样本依赖性,我们开启的进程数越多,对正确率的影响也越大,错误率随着进程数的增大不断增加。
算法参数调整分析
1.不同训练周期数
测试机器硬件型号:
cups:8核 Intel® Core™ [email protected]
固定参数设置:
测试样本:1w 训练样本:6w学习率:0.5 线程/进程数:8 粒度:10 隐藏层细胞:100
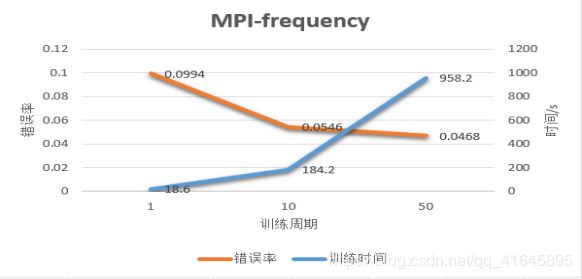
在当我们不断加大训练周期的时候,不论采用哪种并行算法都是时间开销呈线性递增,识别的成功率也会有所增长。但是当训练周期达到一定的值的时候,正确率的提升微乎其微,似乎达到了一个极限,这个时候就不是单凭加大训练量就能继续提高正确率的,需要我们去改善训练所用的算法,例如改变其他参数、更换激活函数、使用卷积神经网络等。
2.不同学习率
测试机器硬件型号:
cups:8核 Intel® Core™ [email protected]
固定参数设置:
测试样本:1w训练样本:6w训练周期:1 线程/进程数:8 粒度:10 隐藏层细胞:100
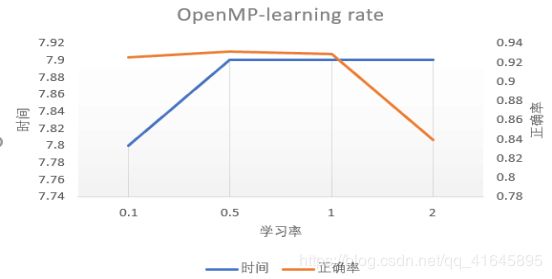
随着学习率的增大,正确率的变化由平缓到线性急速降低,我们可以推测,最优的学习率大致在0-1之间,时间的变化在0.1秒之内,属于正常变化,几乎没有太大影响。
3.不同隐藏层细胞数
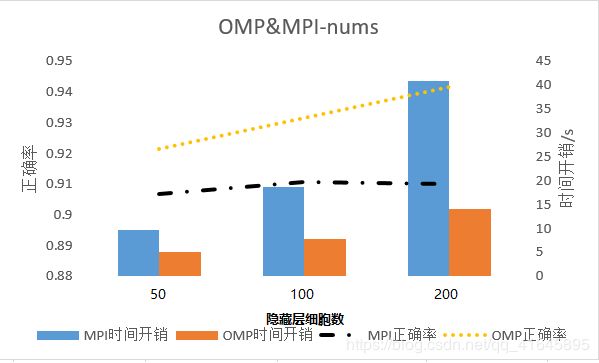
隐藏层细胞数的增加提高了正确率,但是到后面会有所收敛,由于计算量的倍增,时间开销同样也会倍增。
小结
当计算量不足够大,而且网络通信开销比较大的时候,使用OpenMP进行并行优化的效果要比MPI优化的效果更为明显。
同样是在单节点上执行,由于OpenMP是多线程并行,大多数的数据是共享的,每一个线程的计算是独立的、互不干扰的,因此在数据传递上就比MPI的多线程,数据不共享体现出了优势,有效的减小了通信的开销占比。当然,我们在多节点执行的时候,其中一个节点使用了虚拟机,有可能也是程序执行时间被拖慢的原因之一。
这并不是说MPI与OpenMP相比就失去了优势,这只能说明OpenMP更适合于我们这次所选的课题。MPI的优势在于,可以将多台机器组建成一个集群,而不是局限于单台机器。
这是本黑菜第一次写博客,如果文章里哪里出现了学术上的问题,还请各位大佬及时指正,谢谢。
参考资料
https://blog.csdn.net/a493823882/article/details/78683445
https://blog.csdn.net/xbinworld/article/details/74781605
CSDN下载
https://download.csdn.net/download/qq_41645895/11068914