动态开点线段树

学了一个小知识点——动态开点。感觉挺有意思，对于线段树的短板：空间，有挺好的补足作用。
前置知识: 熟练掌握的[线段树]，最好了解一点点的[权值线段树=>其实就是主席树]

动态开点线段树

在一些计数问题中，线段树用于维护值域(一段权值范围)，这样的线段树也称为权值线段树。为了降低空间复杂度，我们可以不建出整棵线段树的结构，而是在最初只建立一个根节点，代表整个区间，当需要访问线段树的某棵子树(某个子区间)时，再建立代表这个子区间的节点。采用这种方法维护的线段树称为动态开点的线段树。

看似很高级，但数据结构这东西没有什么是几张图不能解决的，几张不够，那就再来几张 (实际上够了)
First:对于一个值域，他的范围会很大，比如0–1e9，如果，强行开一个维护值域的线段树（即主席树），对于任意线段树，它大概长成下面这个样子。理想化一点，哪怕它最后是一个满二叉树，最后一层1e9个结点，整棵树2e9个结点，最后，因为是主席树，你还要开n个线段树的大小，总空间变为2e9$\cdot$n （你家编译器数组能开这么大？） ，理想化后数组都开不下了，更别说一般情况还要多往下再留一层空间放着装不下的结点。

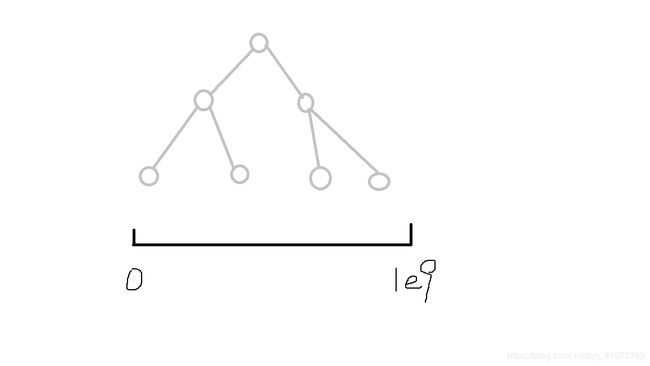
Second:但是熟练掌握线段树的小朋友们不知道在做线段树题的时候有没有这样的感觉，先建一棵树，可是，对于一个询问，我们只是需要从根遍历到叶子结点，有时求区间最值时连叶子结点都不用遍历，如下图：询问第i个叶子结点（深黑色是需要的点，浅色是不需要用到的点）。
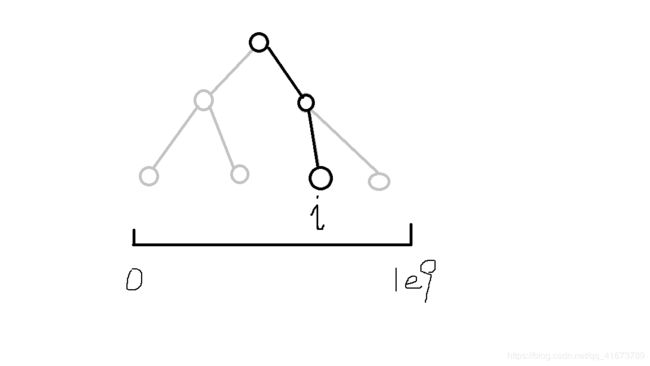Third：因为树上的任意一条链长度平均约为log2(N)，所以对于任意的操作，我们一直都是在一条长度 d<=log2(维护值域的最大值=N) 的链上进行操作。我们所需要的数据就在这条链上，即链上所有结点所储存的信息。所以我们能否考虑对于一棵线段树，暂时先不建出树，只要做题时我们心里知道此处有一棵树，等到要用某一个结点信息时，再将这个要用的结点建出来。答案当然是肯定的。因为我们依然使用线段树维护值域，所以时间复杂度依然是普通线段树的复杂度，即q$\cdot$log2(n){q次询问，每条链长度约log2(n)}。空间复杂度优化后变为了q$\cdot$log2(n){同时间复杂度}

Practice 列队[洛谷P3960]

不要被紫色标签吓到了，这可以作为动态开点线段树最合适不过的板子了，只不过开了是多个线段树而已（咳咳，那不就是主席树了）。

样例输入：

2 2 3
1 1
2 2
1 2

样例输出

1
1
4

分析

第一步：我们所操作的是一个长相很规整的的矩形，根据题目的操作要求，我们可以将其分为n+1个区间，即nm的矩形分为，n(m-1)的矩形和1*n的矩形，红色的矩形每一行算作一个区间，最后蓝色的一列独自成为一个区间，一共n+1个区间。每我们的操作就是从所有红区间中，当输入x,y时，即代表我们要将第x的红区间的第y个数取出来，我们记作A，[y+1,m]的数往前挪一位，然后蓝区间的第x个数就会空出，然后将蓝区间的[x+1,n]的数往前挪一位，蓝区间的最后一位，也就是整个矩形的右下角会空出，最后，将A放入右下角这个空即可，具体过程见图例：

图例（x,y）=（1，1），(2，2)，(1，2)

第二步：我们因为此时的区间不是在移动就是在提取，所以是维护区间，所以自然想到了线段树，因为是维护多个区间，并且(1)每个数都是在$[1,（3\times 1e5-1）+3\times 1e5]的范围内，即值域范围$(2)有多个区间，即多个根。所以此时要用到主席树。（本质还是线段树）。现在我们考虑对于单个点的修改，见下图：

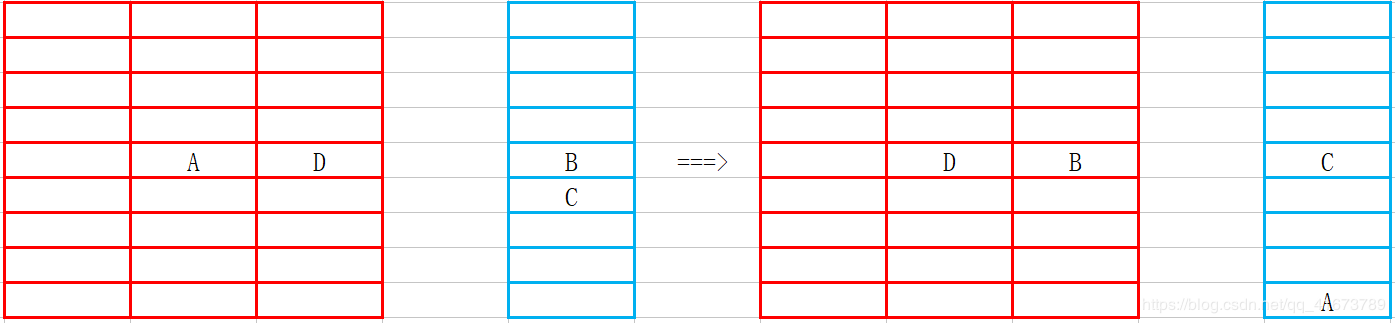
第三步：一个区间约有n个数，如果每个数都往前挪一位，q次询问，每次询问带有n次挪移，时间复杂度显然花式凉凉 ? 。那么我们考虑不挪动，而是给即将空出来的位置打上标记，表示这个数已经被用过，因为区间最后会再加一个数进来，所以区间长度不变。听不懂，没事，有图：两种方式最后留下的区间等价

第四步：到这里也就讲得差不多了，（纳尼！？！？！连动态开点都没讲到，就差不多了！？！？） ，最后考虑一下空间，即动态开点优化。为什么要用动态开店呢？极限情况下q次插入全都插入同一区间，即一个区间长度要开到（n+q），但n+1个线段树，即n+1个区间，所以总空间至少要开到(n+1)$\times$(n+q)? 数据很友好，如果你家电脑是2050年产的那空间就不在我们的讨论范围内 ,:)我们用动态开点来分析一下空间呢？q次询问，但是因为每个区间长度约为n，所以每次开点都只会新出现log2(n)个新点，空间复杂度$q\times$log2(n)。（此时数据露出了善意的微笑 ?）

细节处理请见代码或留言：

#include 
#include 
#define Int register int
typedef long long LL;
using namespace std;
const int N = 3e5 + 5;

static inline char Get_Char() {  
	static char buffer[100000], *S = buffer, *T = buffer;
	if (S == T) {
		T = (S = buffer) + fread(buffer, 1, 100000, stdin);
		if (S == T) return EOF;
	}
	return *S++;
}

//以上是fread快读，没有必要，只是笔者习惯，若要变成普通快读，打开下方的define即可 
//#define Get_Char() getchar()

static inline int Read() {
	int f = 1, x = 0;
	register char sign = Get_Char();
	for (; sign > '9' || sign < '0'; sign = Get_Char())
		if (sign == '-') f = -1;
	for (; sign >= '0' && sign <= '9'; sign = Get_Char())
		x = (x << 3) + (x << 1) + (sign ^ 48);
	return x * f;
}

struct node {
	int lson, rson, Size; //左右儿子根节点 和 当前区间范围内有多少个数没被标记 
	LL val;
	node (){}
	node(const int Lson, const int Rson, const int Size_, const LL Val) :
		lson(Lson), rson(Rson), Size(Size_), val(Val){} 
}seg[(N * 20) + 5]; // Q * log2(N) 
int Cnt_seg; //记录出现多少结点 
 
int now, n, m, q;
int Insert[N + 1], rt[N + 1];// Q+1 N==Q N+1
//Insert[i]记录第i棵树插入了多少个新数
//rt[i]记录第i棵树的根节点，便于执行递归
 
inline int Get_length(const int l, const int r) {
	if (now == n + 1) {
		if (r <= n) return r - l + 1;
		if (l <= n) return n - l + 1;
		return 0;
	}
	if (r < m) return r - l + 1;
	if (l < m) return (m - 1) - l + 1;
	return 0; 
}

inline LL query(int &root, const int l, const int r, const int pos) { // 在根为root的树的区间[l,r]中提取第pos个点 
	if (!root) { //动态开新点 
		root = ++Cnt_seg;
		seg[root].Size = Get_length(l, r);
		if (l == r) {
			if (now == n + 1)
				seg[root].val = 1ll * l * m;
			else 
				seg[root].val = 1ll * (now - 1) * m + l;
		}
	}
	seg[root].Size--; //当前区间有一个数将被提取，总数-1 
	if (l == r) return seg[root].val;
	const int mid = (l + r) >> 1;
	
	//左儿子没有被标记的点的数量 
	if ((!seg[root].lson && Get_length(l, mid) >= pos) || seg[seg[root].lson].Size >= pos) 
		query(seg[root].lson, l, mid, pos);
	else {
		int Const;
		if (!seg[root].lson) Const = Get_length(l, mid);
		else Const = seg[seg[root].lson].Size;
		return query(seg[root].rson, mid + 1, r, pos - Const); 
	}
}

inline void modify(int &root, const int l, const int r, const int pos, const LL num) {
	if (!root) { //动态开新点
		root = ++Cnt_seg;
		seg[root].Size = Get_length(l, r);
		if (l == r) {
			seg[root].val = num;
		} 
	} 
	++seg[root].Size; //当前区间末尾将插入一个新数，总数+1 
	if (l == r) return ;
	int mid = (l + r) >> 1;
	if (pos <= mid) modify(seg[root].lson, l, mid, pos, num);
	else modify(seg[root].rson, mid + 1, r, pos, num);
}

int main() {
	n = Read(), m = Read(), q = Read();
	LL Ans;
	const int Max = max(n, m) + q; // 横着的红区间和竖着的蓝区间长度不一，取最大值，避免越界 
	for (Int i = 1, x, y; i <= q; ++ i) {
		x = Read(), y = Read();
		if (y == m) {
			now = n + 1;
			Ans = query(rt[now], 1, Max, x);
		} else {
			now = x;
			Ans = query(rt[now], 1, Max, y);
		} 
		
		printf("%lld\n", Ans);
	
		now = n + 1;
		modify(rt[now], 1, Max, n + (++Insert[now]), Ans);
		
		if (y != m) {
			Ans = query(rt[now], 1, Max, x);
			now = x; 
			modify(rt[now], 1, Max, m - 1 + (++Insert[now]), Ans);
		}
	}
	return 0;
}