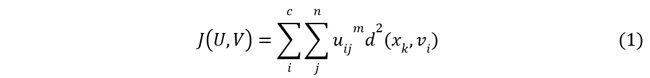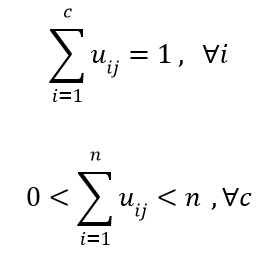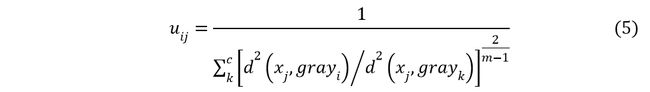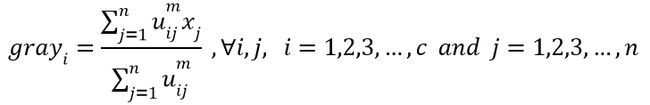K均值、模糊C均值、直觉模糊C均值的理解与C++实现

最近做课题想到用聚类算法做图像分割，从理论到实践，好不容易把理论看完，大概明白是个什么意思，到了代码转化的步骤，what the fuck！！！这都是什么，自己不会编就算了，把别人的代码借过来根本看不懂在写什么！！！特此开贴记录坑爹玩意儿。

---

1、K-means

kmeans应该是算比较简单的算法之一了。算法思想如下：

参考https://blog.csdn.net/loveliuzz/article/details/78783773

代码下载：https://download.csdn.net/download/qq_41828351/11012346

1、随机选取k个中心点

2、遍历所有数据，将每个数据划分到最近的中心点中，这边有个隶属度的概念，每个样本对最近的那个中心点的隶属度为1，记为Uij，意思是样本i对中心j的隶属度为1.

3、计算每个聚类的平均值，并作为新的中心点

重复上述2、3步骤直到终止。有三个终止条件，当迭代的次数到达设定值，最小平方误差小于阈值，簇的中心点的变化率小于阈值，往往在实际代码中使用迭代次数和最小平方误差作为终止条件。

下面是每次迭代过程中需要计算的目标函数和更新的中心点方法，也是该方法中需要实现的关键内容

看起来很简单，目标函数其实就是每个样本到中心点的距离，也可用二范数表示；簇的中心也就是等于属于该簇的所有样本的坐标和的均值。如果是二维坐标那就分为X和Y两部分来计算。

用在图像分割当中，那就不是用坐标，实际上使用的是每个像素点的灰度值作为样本。Kmeans的实现在OpenCV中是有的，只需要调用就可以了，但是在使用前需要将图片的像素整合成一个数字矩阵，矩阵的每一行代表一个像素，如果是3通道，那么该矩阵的大小为（img.cols * img.rows）* 3。

kmeans(samples, //样本
        clusterCount, //聚类数
        labels, //输出的标签，我们需要根据这标签完成自定义操作
		cv::TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 10, 1.0),
		3, //执行次数
		cv::KMEANS_PP_CENTERS, //随机初始化的方法
		centers //输出最终的均值点
	);

 

---

2、Fuzzy-Cmeans

模糊C均值中的模糊是什么意思呢？上面的K均值的隶属度要么为1要么为0，也就是说点X1只能同时确定属于一个中心点，这其实是很不科学的。模糊描述的是一个不确定性，直白的来说我既有机会可以属于你，也有机会可以属于他，这中间是有不确定性的，这个不确定性在聚类法中就体现为隶属度。

参考https://blog.csdn.net/liyuefeilong/article/details/43816495

详细公式推导https://blog.csdn.net/einsdrw/article/details/37930331

详细解释的代码的下载地址：https://download.csdn.net/download/qq_41828351/11012393

FCM原理

根据聚类的数目C和一组包含n个L维向量的数据Xk,用FCM算法输出元素的隶属度uij,它代表着数据xj是属于第i个类的概率。我们的最终目标是要最小化下面的式子(1)，通常取m=2。

其中约束条件为：

2个约束的意思为每个样本对聚类中心的隶属度的和应该为0，每个样本对单个聚类中心的隶属度应该小于1。

以下是更新后的模糊隶属度和聚类中心：

算法流程：

1)  设置目标函数的精度e，模糊指数m（m通常取2）和算法最大迭代次数；

 2)  初始化隶属度矩阵或聚类中心；

3)  由式(2)(3)更新模糊划分矩阵和聚类中心；

4)  若目标函数的差值小于阈值则迭代结束；否则，跳转执行第三步；

5)  根据所得到的隶属度矩阵，取样本隶属度最大值所对应类作为样本聚类的结果，聚类结束。

优缺点：

FCM算法优越于传统硬C均值聚类算法在于隶属度可以连续取值于 [0,1]区间，考虑到了样本属于各个类的“亦此亦彼”性，能够对类与类之间样本有重叠的数据集进行分类，具有良好的收敛性；而且FCM算法复杂度低，易于实现。然而，FCM也存在着不足之处，如目标函数在迭代过程中容易陷入局部最小、函数收敛速度慢、对初始值、噪声比较敏感等问题。下面从分析模糊C均值聚类划分矩阵的隶属度的含义、划分趋势出发，讨论一种可以改善FCM性能的算法——IFCM算法。在此之前需要引入新的概念，即直觉模糊集。

---

3、直觉模糊C均值 IFCM

直觉模糊集(IFS)作为模糊集的重要拓展，通过增加新的属性参数——非隶属度γ和不确定度π，从而更加细腻地刻画客观世界的模糊性质，假设直觉模糊集A表示了样本x与论域X={x1,x2,…,xn }的关系，有：

对于传统的模糊算法，非隶属度只是作为隶属度的补而存在，但是在IFS中，同时考虑了隶属度、非隶属度和不确定度的作用，使得非隶属度的定义和一般的模糊算法不同。直觉模糊C均值聚类算法引入了不确定度这个概念。这是因为在聚类过程中，分类方式取决于人的选择，所以分类方式带来的隶属度是不确定的，在缺乏明确定义的分类方式的时候会有不确定的因素。

参考：https://blog.csdn.net/liyuefeilong/article/details/43816495

IFCM代码下载：https://download.csdn.net/download/qq_41828351/11012402

融入局部信息的直觉模糊C均值IFS_FCM代码下载：https://download.csdn.net/download/qq_41828351/11012402

在IFCM中引入了直觉模糊熵（IFE）

IFCM算法实现：

 

对于IFCM算法中不确定度的参数α的取值，图2，3，4分别给出α=0.5,α=0.7和α=0.85时的分割效果。当取α=0.5或更小时，灰度图像无法得到适当的分割效果；当α=0.7时可以输出分割图像，而若α取0.8或更高时，分割的效果更好。本实验选定α=0.85作为经验值。

优缺点：

IFCM算法是FCM算法的推广，它继承了FCM的主要优点：算法设计简单，可转化为优化问题、算法复杂度低。而FCM算法的一些缺点在IFCM算法中同样存在，如在计算目标函数时易陷入局部最小、聚类数目需要事先确定等等。

直觉模糊C均值聚类(IFCM)算法在FCM的基础上引入关键的不确定度 ，使得图像分割在图像噪声的滤除和图像的细节保留之间取得平衡。因此该算法理论上能改善图像分割中的噪声问题，但现实中对于不同图像的分割效果各异。而对于无严重噪声污染的图像，IFCM与FCM的处理效果并没有太大的区别。不确定度中参数取的是经验值，因此参数的选取是否是最优值有待进一步的验证。总体上，IFCM算法的性能要优于FCM算法。

---

模糊隶属度矩阵在图像分割的意义：

模糊隶属度可以用于表示一幅灰度图像中的某一像素点属于某个灰度中心的程度，只需要寻找像素点对某灰度值中心的最大隶属度，即可将该像素点划分到该灰度级的区域中去。