统计学习方法(4) GBDT算法解释与Python实现
回归树
统计学习的部分也差不多该结束了,我希望以当前最效果最好的一种统计学习模型,Xgboost的原型GBDT来结尾。
GBDT的基础是CART决策树。在CART基学习器上使用boosting,形成更好的集成学习器,就是GBDT的思想。CART在离散特征上的表现并不特别,也就是把我们之前学过的C4.5树用基尼系数划分。但在连续特征上使用树算法进行拟合回归就并没有那么轻松,一是划分标准不容易确定,二是决策树的本质决定了决策树容易过拟合。但总之,我们还是先尝试实现用CART树来做常见的回归预测。
CART回归树预测回归连续型数据,假设X与Y分别是输入和输出变量,并且Y是连续变量。在训练数据集所在的输入空间中,递归的将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树。
![]()
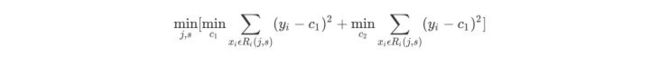
考虑对一组数据,寻找一个合适的常数C表征数据让MSE最小,则C就是样本均值。由此,回归树的生成方法就是遍历所有N个样本的N-1个划分点,计算划分后两类数据的MSE。找到最优划分处。反复迭代划分就是最小二乘回归树。

import numpy as np
import random
from copy import deepcopy
import matplotlib
from matplotlib import pyplot as plt
from sklearn.metrics import accuracy_score
import warnings
warnings.filterwarnings('ignore')
首先生成数据用于回归
X_train = np.linspace(1,5,100)
y_train = 10*np.log(X_train)
#加噪声
y_train += np.random.randn(100)
plt.scatter(X_train,y_train)
X_train = X_train.reshape(-1,1)
class Node:
def __init__(self):
self.dim = None #dimension ,划分特征维度
self.mid = None #middle,划分中值点
self.y = None #结点预测返回值
self.left = None
self.right = None
def grow(self, X, y, max_depth = 5):
'''
根据数据X和y进行划分点选取
参数max_depth是还允许向下生长的层数
'''
self.y = np.mean(y)
#划分点选择需要遍历所有元素的所有中值点
N,M = X.shape
if max_depth == 0:
return
if N<5:
return
winner = (0,0)
win_error = float("inf")
for dim in range(M):
args = np.argsort(X[:,dim])
X = X[args]
y = y[args]
X_dim = X[:,dim]
for ii in range(N-1):
mid = 0.5*(X_dim[ii]+X_dim[ii+1])
y_left_mean = np.mean(y[:ii+1])
y_left_MSE = np.sum((y[:ii+1]-y_left_mean)**2)
y_right_mean = np.mean(y[ii+1:])
y_right_MSE = np.sum((y[ii+1:]-y_right_mean)**2)
err = y_left_MSE+y_right_MSE
if err<win_error:
win_error = err
winner = (dim,mid)
#完成遍历之后将会找到一个合适的dim和mid进行划分
X_left = []
y_left = []
X_right = []
y_right = []
self.dim,self.mid = winner
for i in range(N):
if X[i][self.dim]<self.mid:
X_left.append(X[i])
y_left.append(y[i])
else:
X_right.append(X[i])
y_right.append(y[i])
X_left = np.array(X_left)
y_left = np.array(y_left)
X_right = np.array(X_right)
y_right = np.array(y_right)
if len(X_left)==0 or len(X_right)==0:
return
self.left = Node()
self.left.grow(X_left,y_left,max_depth-1)
self.right = Node()
self.right.grow(X_right,y_right,max_depth-1)
def predict(self, x):
'''
预测函数,如果有子结点就下溯,没有就返回self.y
'''
if self.left == None:
return self.y
if x[self.dim]<self.mid:
return self.left.predict(x)
else:
return self.right.predict(x)
tree = Node()
tree.grow(X_train,y_train,3)
y_pred = [tree.predict(x) for x in X_train]
X_train = X_train.reshape(-1)
plt.scatter(X_train,y_train,c='y')
plt.plot(X_train,y_pred,c='r')
X_train = X_train.reshape(-1,1)
#希望模型学习一个函数, f(x1,x2) = sin(x1)cos(x2)
#生成伪数据集
row = np.linspace(0,2,10)
col = np.linspace(0,2,10)
x1,x2 = np.meshgrid(row,col)
X = np.concatenate((x1.reshape(1,-1),x2.reshape(1,-1)),axis=0).T
y = np.zeros(100)
for i in range(len(X)):
y[i] = (X[i][0]+X[i][1])**2
tree = Node()
tree.grow(X,y,8)
#用3dplot打印model生成的曲面
from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import pyplot as plt
xx = np.linspace(0,2,100)
yy = np.linspace(0,2,100)
X,Y = np.meshgrid(xx,yy)
Z = np.zeros(X.shape)
for i in range(len(X)):
for j in range(len(X[0])):
x = np.array((X[i][j],Y[i][j]))
Z[i][j] = tree.predict(x)
fig = plt.figure()
axes3d = Axes3D(fig)
axes3d.plot_surface(X,Y,Z,color='grey')

调整深度参数和剪枝可以有效控制过拟合。如果想要更精确,更强大的预测,我们有一种借助boosting提升的方法,就是下面的的GBDT,Gradient Boosting Decision Tree:梯度提升决策树
GBDT
有了回归树做基学习器,就能用集成方法增强树模型。Freidman提出了梯度提升算法:利用最速下降的近似方法,即利用损失函数的负梯度在当前模型的值,作为回归问题中提升树算法的残差的近似值,拟合一个回归树。(注:鄙人私以为,与其说负梯度作为残差的近似值,不如说残差是负梯度的一种特例)算法如下(截图来自《The Elements of Statistical Learning》)

import numpy as np
import random
from copy import deepcopy
import matplotlib
from matplotlib import pyplot as plt
from sklearn.metrics import accuracy_score
import warnings
warnings.filterwarnings('ignore')
class Node:
def __init__(self):
self.dim = None #dimension ,划分特征维度
self.mid = None #middle,划分中值点
self.y = None #结点预测返回值
self.left = None
self.right = None
def grow(self, X, y, max_depth = 5):
'''
根据数据X和y进行划分点选取
参数max_depth是还允许向下生长的层数
'''
self.y = np.mean(y)
#划分点选择需要遍历所有元素的所有中值点
N,M = X.shape
if max_depth == 0:
return
if N<2:
return
winner = (0,0)
win_error = float("inf")
for dim in range(M):
args = np.argsort(X[:,dim])
X = X[args]
y = y[args]
X_dim = X[:,dim]
for ii in range(N-1):
mid = 0.5*(X_dim[ii]+X_dim[ii+1])
y_left_mean = np.mean(y[:ii+1])
y_left_MSE = np.sum((y[:ii+1]-y_left_mean)**2)
y_right_mean = np.mean(y[ii+1:])
y_right_MSE = np.sum((y[ii+1:]-y_right_mean)**2)
err = y_left_MSE+y_right_MSE
if err<win_error:
win_error = err
winner = (dim,mid)
#完成遍历之后将会找到一个合适的dim和mid进行划分
X_left = []
y_left = []
X_right = []
y_right = []
self.dim,self.mid = winner
for i in range(N):
if X[i][self.dim]<self.mid:
X_left.append(X[i])
y_left.append(y[i])
else:
X_right.append(X[i])
y_right.append(y[i])
X_left = np.array(X_left)
y_left = np.array(y_left)
X_right = np.array(X_right)
y_right = np.array(y_right)
if len(X_left)==0 or len(X_right)==0:
return
self.left = Node()
self.left.grow(X_left,y_left,max_depth-1)
self.right = Node()
self.right.grow(X_right,y_right,max_depth-1)
def predict(self, x):
'''
预测函数,如果有子结点就下溯,没有就返回self.y
'''
if self.left == None:
return self.y
if x[self.dim]<self.mid:
return self.left.predict(x)
else:
return self.right.predict(x)
这里用均方误差作为损失函数,从而梯度就是残差y-f(x)
class GBDT:
def __init__(self, max_num = 5, max_depth = 6):
self.num = max_num
self.depth = max_depth
self.trees = []
def fit(self, X, y):
X_train = X.copy()
y_train = y.copy()
for _ in range(self.num):
tree = Node()
tree.grow(X_train,y_train,self.depth)
for i in range(len(X)):
X_train[i] -= tree.predict(X_train[i])
self.trees.append(tree)
def predict(self, x):
return sum(tree.predict(x) for tree in self.trees)
首先生成数据用于回归
X_train = np.linspace(1,5,100)
y_train = np.log(X_train)+np.sin(X_train)
#加噪声
y_train += np.random.randn(100)*0.1
plt.scatter(X_train,y_train)
X_train = X_train.reshape(-1,1)
model = GBDT(max_num=20,max_depth=6)
model.fit(X_train,y_train)
y_pred = [model.trees[0].predict(x) for x in X_train]
X_train = X_train.reshape(-1)
plt.scatter(X_train,y_train,c='y')
plt.plot(X_train,y_pred,c='r')
X_train = X_train.reshape(-1,1)
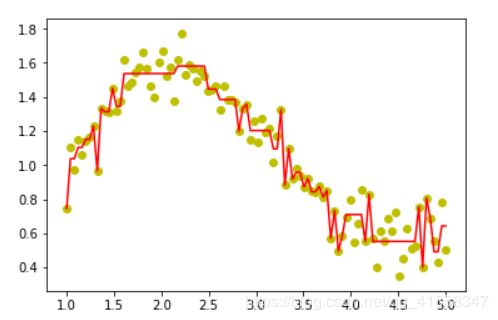
可以看出非常强大的拟合能力,而GBDT的潜力远不止拟合。其具有天然优势可以发现多种有区分性的特征以及特征组合。业界中,Facebook使用其来自动发现有效的特征、特征组合,来作为LR模型中的特征,以提高 CTR预估(Click-Through Rate Prediction)的准确性(详见参考文献);GBDT在淘宝的搜索及预测业务上也发挥了重要作用(详见参考文献)。 《Practical Lessons from Predicting Clicks on Ads at Facebook》
另外,GBDT也在分类问题里发挥作用。只要我们用one-hot编码类别,然后对每个类别训练一个GBDT来预测类别的y值,就能近似实现多分类问题。我们用下面这个iris的例子来说明。
from sklearn.datasets import load_iris
iris = load_iris()
descr = iris['DESCR']
data = iris['data']
feature_names = iris['feature_names']
target = iris['target']
target_names = iris['target_names']
def one_hot(y):
size = np.max(y)+1
out = np.zeros((len(y),size))
for i in range(len(y)):
out[i][int(y[i])] = 1
return out
y = one_hot(target)
X = data
y = y.T
#对每一个类别(这里是3个类别)训练一个GBDT
classifiers = []
for y0 in y:
model = GBDT(max_num=8,max_depth=6)
model.fit(X,y0)
classifiers.append(model)
for x in data:
c = [np.argmax(np.array([classifiers[i].predict(x) for i in range(3)])) for x in data]
right = np.sum(c==target)
print("Accuracy:",right/len(target))
Accuracy: 0.98
这个结果已经相当不错了,由此我们可以看出GBDT今天在数据科学领域火爆的几个原因。一是它的泛用性非常好,既能用于回归又能用于分类。再就是训练快,效果好。并且我们还可以用它筛选特征。今天大量的互联网公司和金融公司都在用GBDT做各种各样的事情。