LeetCode探索:初级算法(数组篇第一刷)
近来打算系统地学习一波数据结构与算法,因此根据LeetCode官方推出地经典面试题目清单开始刷题。本篇文章记录了初级算法中的数组篇,为了追求速度,我先大概地过一遍,每道题没有去分析多种解法,可能不是最优解,仅仅为我做题时的思路,若有什么错误的地方,欢迎大佬们指正哈!
ps:第一次写博客,格式之类的难免有所欠妥,还请大家谅解!
从排序数组中删除重复项
 解法:双指针
解法:双指针
解析:题中数组是有序的,因此重复的值肯定是相邻的,且从第2个值开始才有可能重复,所以遍历数组1~n-1。使用变量cur来作为当前指针,若数组中相邻的值重复,cur保持不变;若数组中出相邻的值不同,则让当前值覆盖cur中的值,cur指向下一个位置。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
if(n == 0) return 0;
if(n == 1) return 1;
int cur = 1;
for(int i = 1; i < n; i++) { //从第二个值开始遍历
if(nums[i] == nums[i-1]) {
continue;
} else {
nums[cur++] = nums[i];
}
}
return cur;
}
};
时间复杂度:O(n) ,遍历一次数组
空间复杂度:O(1), 需要用到常量空间
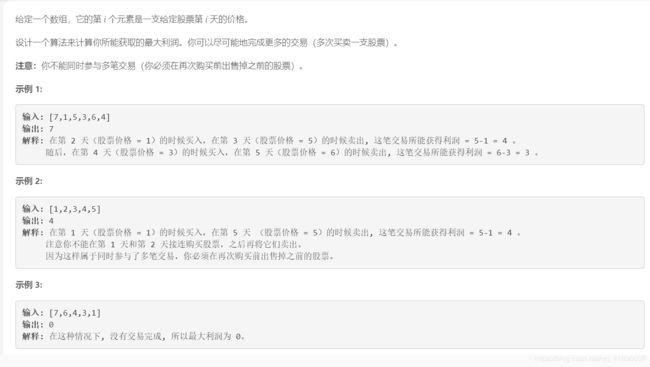
买卖股票的最佳时机 II
解法:贪心算法
解析:所有上涨交易日都买卖(赚到所有利润),所有下降交易日都不买卖(永不亏钱)。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res = 0;
for(int i = 1; i < prices.size(); i++) {
if(prices[i] - prices[i-1] > 0)
res += prices[i] - prices[i-1];
}
return res;
}
};
时间复杂度:O(n) ,遍历一次数组
空间复杂度:O(1), 需要用到常量空间
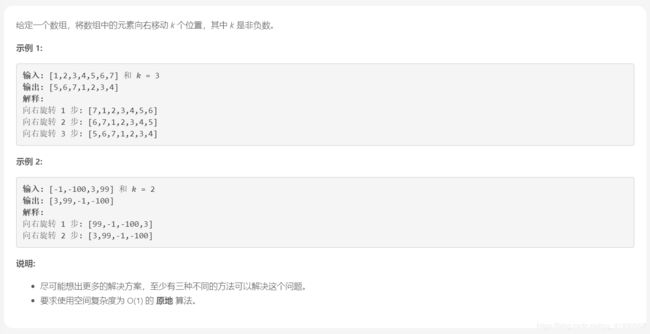
旋转数组
解法:使用反转
解析:这道题要求使用原地算法,因此不能开额外的数组。首先要注意的是k的大小,当k大于数组n的长度时,数组每移动n次,就回到了原来的位置,相当于没有改变位置。可以将k对n取模,减少不必要的时间消耗
ps:接下来我开始循环k次,一位一位地移动位置,结果超时了。后面看了官方题解,看到了一种捷径式解法:反转
超时代码:
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k = k % n;
while(k--) {
int t = nums[n-1]; //最后一位的值
for(int i = n-1; i >= 1; i--) {
nums[i] = nums[i-1];
}
nums[0] = t;
}
}
};
时间复杂度:O(k * n) ,遍历k次数组
空间复杂度:O(1), 需要用到常量空间
官方题解:
原始数组 ------------- : 1 2 3 4 5 6 7
反转所有数字后 ---- : 7 6 5 4 3 2 1
反转前 k 个数字后 - : 5 6 7 4 3 2 1
反转后 n-k 个数字后 : 5 6 7 1 2 3 4 --> 结果
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
if(n == 0) return;
k = k % n;
reverse(nums.begin(), nums.end());
reverse(nums.begin(), nums.begin()+k);
reverse(nums.begin()+k, nums.end());
}
};
时间复杂度:O(n) ,反转3次
空间复杂度:O(1), 需要用到常量空间
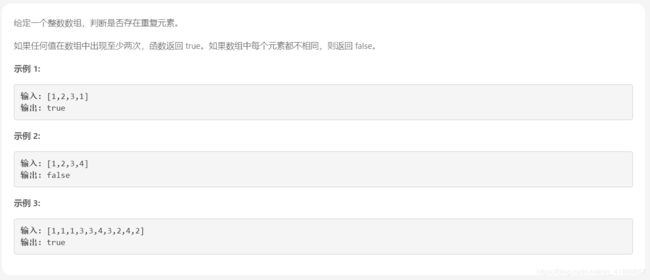
存在重复
解法:排序+遍历
解析:数组排序后重复值肯定是相邻的,做个简单的遍历判断即可
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
int n = nums.size();
if(n == 0 || n == 1) return false; //0或1个元素必定不会重复
sort(nums.begin(), nums.end());
for(int i = 1; i < n; i++) {
if(nums[i] == nums[i-1]) return true;
}
return false;
}
};
时间复杂度:O(n * logn) ,排序的时间复杂度是O(n * logn) ,遍历的时间复杂度是O(n),整个算法的时间复杂度主要由排序决定 。
空间复杂度:O(1), 需要用到常量空间
ps:若想要使用空间换时间消耗的话,可以使用哈希表。
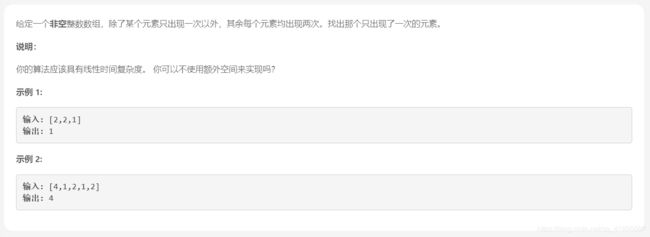
只出现一次的数字
解法:位操作
解析:异或大法好!利用异或的特性(对同一个数异或两次后,相当于没有操作),因此将初始值设定为零,只出现一次的数字对0异或,结果即为这个数字的值!!位运算还是挺重要的呀!有时间还是得多练习一下,可以减少很多麻烦
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res = 0;
for(int i = 0; i < nums.size(); i++) {
res ^= nums[i];
}
return res;
}
};
时间复杂度:O(n) ,遍历一次数组
空间复杂度:O(1), 需要用到常量空间
两个数组的交集
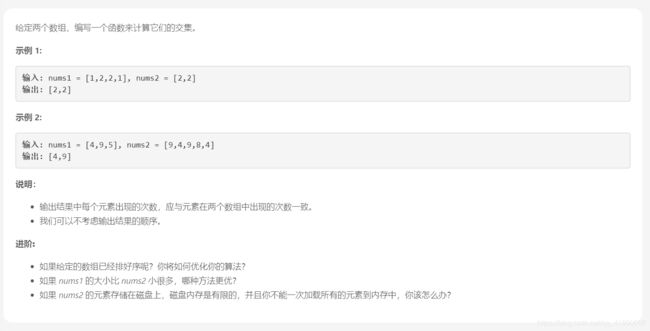
解法:哈希表
解析:建立
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
vector<int> res;
map<int, int> m;
for(int i = 0; i < nums1.size(); i++) {
if(!m.count(nums1[i])) m[nums1[i]] = 1; //键不存在,则赋初始值为1
else m[nums1[i]]++;
}
for(int i = 0; i < nums2.size(); i++) {
if(m.count(nums2[i]) && m[nums2[i]] > 0) //键存在,且数量大于0
res.push_back(nums2[i]), m[nums2[i]]--;
}
return res;
}
};
时间复杂度:O(max(n, m)) n是数组一的大小,m是数组二的大小
空间复杂度:O(n), 需要用到常量空间
ps:这道题我没有考虑去进阶,如n远远大于m时,可以为数组二建立哈希表,减少空间消耗,即空间复杂度可以优化为O(min(n, m)),小伙伴们如果有什么好的解法,欢迎在评论区分享emmmm
加一
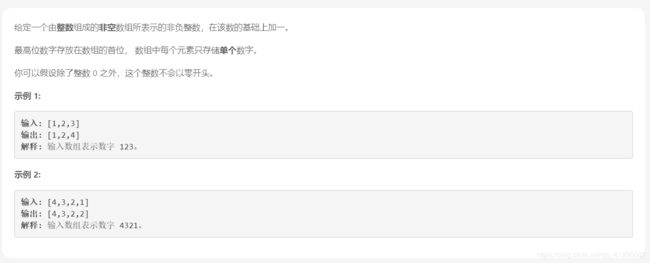
解法:逆序遍历
解析:对数组进行原地修改,从最后一位开始逆序遍历,进行加一和取余操作,若当前值不为0,即不会产生下一个进位,就直接返回结果。考虑到99999这种连续进位的情况,当遍历整个数组后,还没有返回结果时,则在动态数组的第一位插入进位值1,返回最终结果10…00
class Solution {
public:
vector<int> plusOne(vector<int>& digits) {
int n = digits.size();
for(int i = n-1; i >= 0; i--) {
digits[i]++;
digits[i] = digits[i] % 10;
if(digits[i] != 0) return digits;
}
digits.insert(digits.begin(), 1);
return digits;
}
};
时间复杂度:O(n) ,遍历一次数组
空间复杂度:O(1),原地操作,只需要用到常量空间
移动零
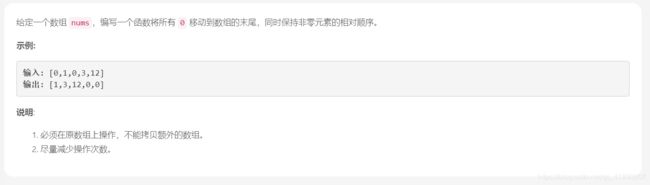
解法:双指针
解析:这道题我的解法与第一道有点类似,使用cur来作为当前指针,并使用cnt来记录当前0的个数
①若存在0,则将nums[i]覆盖为0
②若不存在0,nums[i]即为原始值,cur==i
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int cur = 0, cnt = 0;
for(int i = 0; i < nums.size(); i++) {
if(nums[i] == 0) {
cnt++;
continue;
} else {
nums[cur++] = nums[i];
if(cnt > 0) nums[i] = 0;
}
}
}
};
时间复杂度:O(n) ,遍历一次数组
空间复杂度:O(1),需要用到常量空间
两数之和

唠叨:作为LeetCode的第一道题,大家应该也是印象深刻吧!想当初因为不太习惯使用vector并且用函数来解决问题,第一道题拖了n久才去提交(还是使用暴力……),很多事情,从0到1,真的是很重要的一个过程了!比如这篇博客,写得一点都不香~
解法:遍历+哈希表
解析:此题我的解法是在遍历过程中判断哈希表中的值,实现一次遍历即可得出结果。键代表数组元素的值,值为该元素值的下标
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
map<int, int> mapp;
vector<int> res;
for(int i = 0; i < nums.size(); i++) {
if(mapp.count(target-nums[i])) {
res.push_back(mapp[target-nums[i]]);
res.push_back(i);
return res;
}
mapp[nums[i]] = i; //这条语言必须放在if之后
//防止因为相同的值,下标被重新覆盖
}
return res;
}
};
时间复杂度:O(n) ,遍历一次数组
空间复杂度:O(n),哈希表的线性空间复杂度
有效的数独
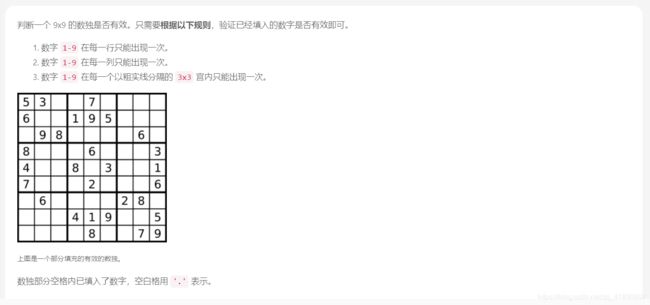
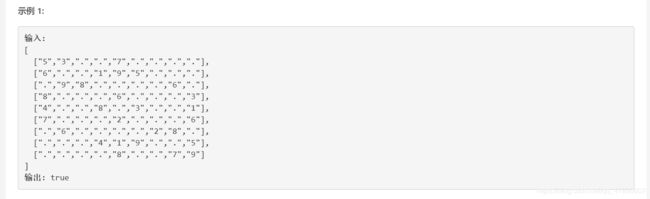
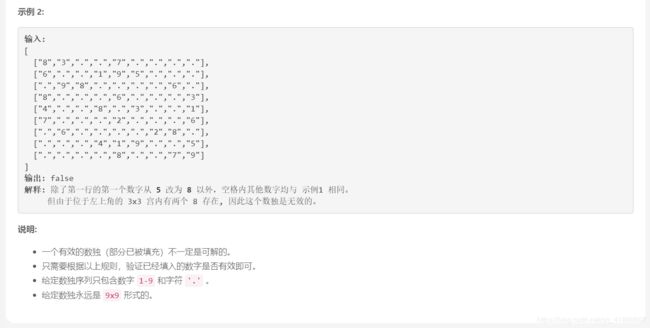
解法:遍历+哈希表
解析:将大宫格分为9个小的9宫格
建立三个哈希表数组
①行 :i
每次遍历时判断当前行的哈希表是否有相同的数
②列 :j
每次遍历时判断当前列的哈希表是否有相同的数
③宫格:(i / 3) * 3 + (j / 3)
每次遍历时判断当前宫格的哈希表是否有相同的数
借用一下leetcode的分析图:
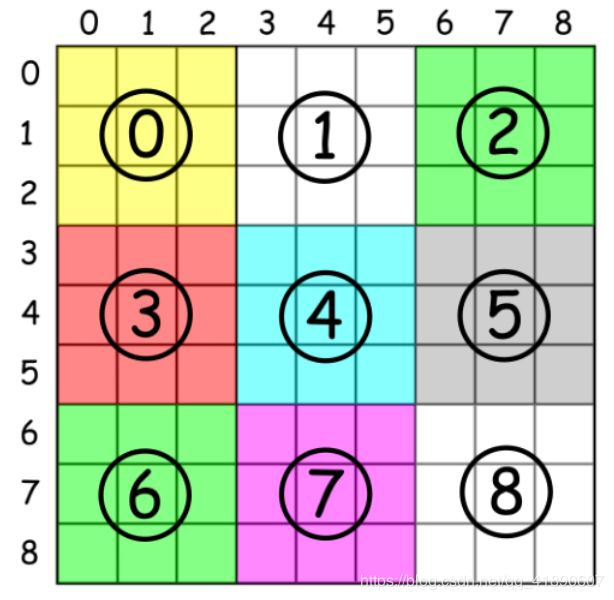
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
map<int, int> row[9], col[9], box[9];
for(int i = 0; i < 9; i++) {
for(int j = 0; j < 9; j++) {
if(board[i][j] >= '0' && board[i][j] <= '9') {
int x = board[i][j] - '0';
//若其中任意一个条件,则不是有效的数独
if(row[i].count(x) || col[j].count(x) || box[(i/3)*3 + j/3].count(x))
return false;
row[i][x] = 1;
col[j][x] = 1;
box[(i/3)*3 + j/3][x] = 1;
}
}
}
return true;
}
};
时间复杂度:O(1)
空间复杂度:O(1)
ps:这道题的时间复杂度和空间复杂度可能会有一些争议,但是81个单元格和27个map是固定的,也就是常数值,不会随输入的改变而改变
旋转图像
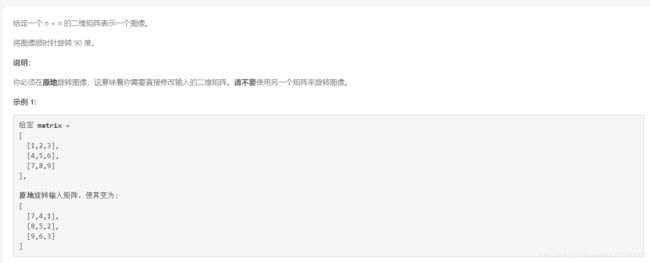

解法:自外向内,顺时针旋转四个值
解析:话不多说,看图

首先是最外一圈,旋转这4个数的值
①15 -> t ②16 -> 15 ③11 -> 16 ④5 -> 11 ⑤ t -> 5
依次类推……


再进入内圈

class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
int cur = 0; //当前圈第一个元素的行与列
while(cur < n/2) {
for(int i = cur; i < n-cur-1; i++) {
int t = matrix[n-i-1][cur];
matrix[n-i-1][cur] = matrix[n-cur-1][n-i-1];
matrix[n-cur-1][n-i-1] = matrix[i][n-cur-1];
matrix[i][n-cur-1] = matrix[cur][i];
matrix[cur][i] = t;
}
cur++;
}
}
};
时间复杂度:O(n^2),两重循环
空间复杂度:O(1),需要用到常量空间
ps:这道题还有另一种解法,但是相对没有那么容易想到
解法:转置+翻转
解析:转置矩阵(交换matrix[i][j] 和 matrix[j][i]的值),翻转每一行
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for(int i = 0; i < n; i++) {
for(int j = 0; j < i; j++) {
int t = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = t;
}
}
for(int i = 0; i < n; i++) {
reverse(matrix[i].begin(), matrix[i].end());
}
}
};
时间复杂度:O(n^2),转置和反转都需要用到n的平方
空间复杂度:O(1),需要用到常量空间
总结:
数组类型的问题目前用得比较多的解法是双指针、排序、位操作、哈希表和贪心算法,还是得具体问题具体分析,因此多实践是很重要的。由于线性代数学得不扎实,一些矩阵的特性不太了解,以后遇到旋转或移动的问题,没有思路的时候可以考虑一下倒置和反转hh。