回溯算法——从LeetCode题海中总结常见套路

目录

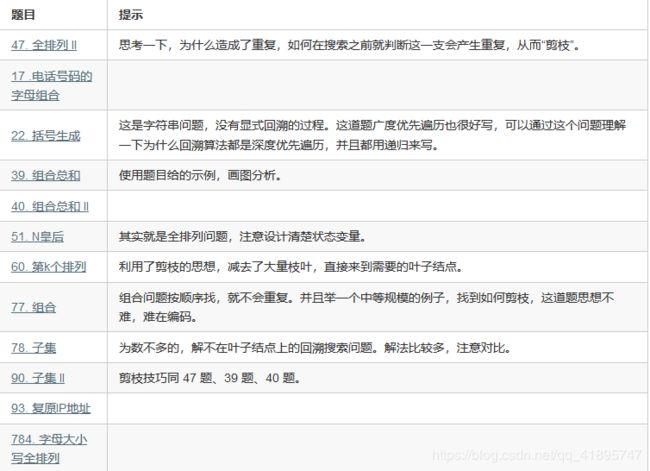
回溯算法简介

算法框架

可重复回溯算法框架

 不可重复回溯算法框架

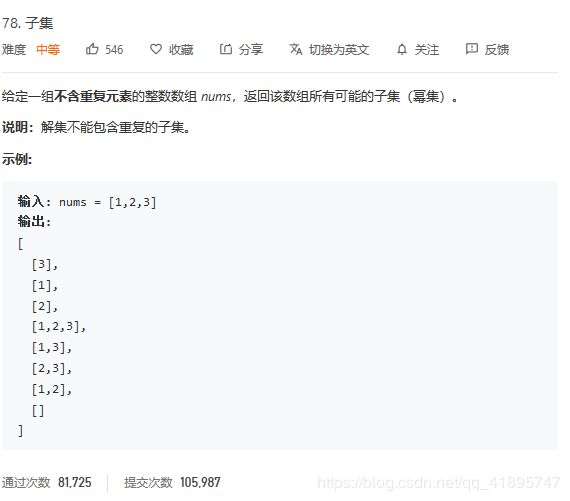
不可重复回溯开胃菜：LeetCode78.子集

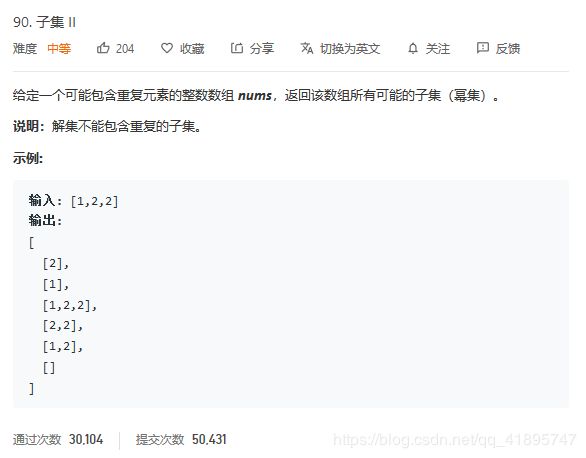
排序+去重的不可重复回溯：LeetCode90.子集II

可重复回溯中选择"不可重复"：LeetCode46.全排列

可重复回溯中选择"不可重复"：LeetCode面试题08.07.无重复字符串的排列组合

模拟“手动全排列”方式的回溯：LeetCode47.全排列II

和上一题全排列II思路一模一样的：面试题 08.08.有重复字符串的排列组合

隐藏的回溯：LeetCode22.括号生成

参考：

---

回溯算法简介

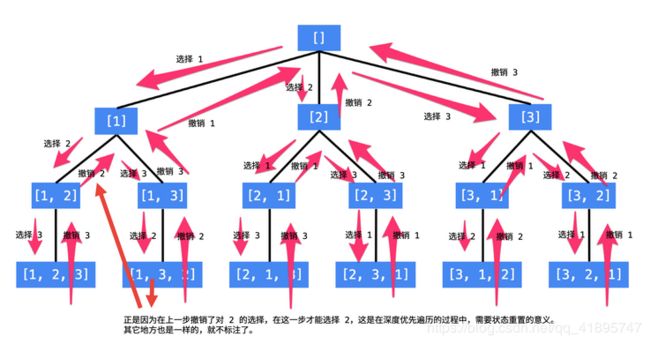
求道不求术，两图胜千言

算法框架

下面以输出[1,2,3]的全排列为例，学习可重复回溯和不可重复回溯算法的框架

可重复回溯算法框架

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

//可重复回溯,相当于
#include 
#include 
#include 
using namespace std;

//打印函数
void print(stack temp){
    stack s(temp);
    while(!s.empty()){
        cout< nums, stack temp){
    if(temp.size()>=3){//可重复回溯
        print(temp);
        return;
    }
    //在选择列表中做选择
    for(int i=0;i nums(a,a+3);
    stack temp;
    backtrack(nums,temp);

    return 0;
}

结果：

111 211 311 121 221 321 131 231 331 112 212 312 122 222 322 132 232 332 113 213 313 123 223 323 133 233 333

 不可重复回溯算法框架

backtrack()
    for 选择 in 选择列表:
        # 做选择
        将该选择从选择列表移除
        路径.add(选择)
        backtrack(路径, 选择列表)
        # 撤销选择
        路径.remove(选择)
        将该选择再加入选择列表

//不可重复回溯,相当于每层进行一次排列组合
#include 
#include 
#include 
using namespace std;

//打印函数
void print(stack temp){
    stack s(temp);
    while(!s.empty()){
        cout< nums, int index,stack temp){
    //在选择列表中做选择
    for(int i=index;i nums(a,a+3);
    stack temp;
    backtrack(nums,0,temp);

    return 0;
}

 结果：

1 21 321 31 2 32 3 

不可重复回溯开胃菜：LeetCode78.子集

完全是前面的index不可重复回溯的框架！！！

class Solution {
private:
    vector> ans;
public:
    vector> subsets(vector& nums) {
        vector temp;
        ans.push_back(temp);
        backtrack(nums,0,temp);
        return ans;
    }
    void backtrack(vector nums,int index,vector temp){
        for(int i=index;i

排序+去重的不可重复回溯：LeetCode90.子集II

如果没有执行排序操作，体会一下：

比如[4,1,4]和[4,4,1]就会当做两个不同的序列！

class Solution {
private:
    vector> ans;
public:
    vector> subsetsWithDup(vector& nums) {
        vector temp;
        sort(nums.begin(),nums.end());//记得先排序
        ans.push_back(temp);
        backtrack(nums,0,temp);
        return ans;
    }
    void backtrack(vector nums,int index,vector temp){
        for(int i=index;i

可重复回溯中选择"不可重复"：LeetCode46.全排列

 

看清楚，这里既不完全是上面的可重复回溯，也不完全是上面不可重复回溯的模板，稍微变通一下即可！

class Solution {
public:
    vector> result;
    vector> permute(vector& nums) {
        vector track;
        backtrack(nums,track);
        return result;
    }
    void backtrack(vector nums,vector track){
        if(track.size()==nums.size()){
            result.push_back(track);
            return;
        }
        for(int i=0;i

可重复回溯中选择"不可重复"：LeetCode面试题08.07.无重复字符串的排列组合

class Solution {
private:
    vector ans;
public:
    vector permutation(string S) {
        string temp;
        // sort(S.begin(),S.end());
        backtrack(S,temp);
        return ans;
    }
    void backtrack(string S,string temp){
        if(temp.size()==S.size()){
            ans.push_back(temp);
            return;
        }
        for(int i=0;i

模拟“手动全排列”方式的回溯：LeetCode47.全排列II

其实这个全排列算法就是固定一个数的位置(left)，然后从下一位数再开始全排列(递归过程)...直到最后一位数，模拟手动全排列的过程。

所以如果要去重的话，只要控制每次排列时，固定的那个数是不一样的就行了。因为固定的数不一样，那从这个数开始产生的全排列就不一样。所以只要让每次的left位置的数不一样就行，所以先sort，保证只有相邻的数是可能一样的，然后

if (i != left && nums[left] == nums[i]) continue;

使得每次固定的数(即left)都不一样.

class Solution {
public:
    vector> ans;
    vector> permuteUnique(vector& nums) {
        sort(nums.begin(),nums.end());
        backtrack(nums,0,nums.size()-1);
        return ans;
    }
    void backtrack(vector nums,int left,int right){
        if(left==right)
            ans.push_back(nums);
        else{
            for(int i=left;i<=right;i++){
                if(i!=left&&nums[left]==nums[i])//去重
                    continue;
                swap(nums[left],nums[i]);
                backtrack(nums,left+1,right);
            }
        }
    }
};

和上一题全排列II思路一模一样的：面试题 08.08.有重复字符串的排列组合

class Solution {
public:
    vector ans;
    vector permutation(string S) {
        sort(S.begin(),S.end());
        backtraver(S,0,S.size()-1);
        return ans;
    }
    void backtraver(string S, int left, int right){
        if(left==right){
            ans.push_back(S);
        }else{
            for(int i=left; i<=right; i++){
                if(i!=left&&S[i]==S[left])
                    continue;
                swap(S[i],S[left]);
                backtraver(S,left+1,right);
            }
        }
    }
};

 

隐藏的回溯：LeetCode22.括号生成

一开始的心情：

lc 和 rc 分别表示左括号的个数和右括号的个数。vector的push_back()方法调用的时候实际上是使用的值传递，也就是会进行赋值到vector里。

https://leetcode-cn.com/problems/generate-parentheses/solution/ru-men-ji-bie-de-hui-su-fa-xue-hui-tao-lu-miao-don/

class Solution {
public:
    vector generateParenthesis(int n) {
        vector ans;
        int lc=0,rc=0;
        backtrack(ans,"",n,lc,rc);
        return ans;
    }
    void backtrack(vector& ans,string path,int n,int lc,int rc){
        if(rc>lc||lc>n||rc>n)
            return;
        if(lc==rc&&lc==n){
            ans.push_back(path);
            return;
        }
        backtrack(ans,path+'(',n,lc+1,rc);
        backtrack(ans,path+')',n,lc,rc+1);
    }
};

参考：

https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/

https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-xiang-jie-by-labuladong-2/

https://www.cnblogs.com/oldhands/p/11840667.html