最优化理论简述
0 概述
优化问题的类型:
NLP:非线性优化
Dynamic Optimization(Optimal Control):与时间有关
Stochastic optimization 随机优化
multi—objective optimization 多目标优化
game-theory 博弈论
==============================================
1 最优化中的概念
凸集(convex sets):两个元素任意线性组合,仍在两个元素所在集合。
凸函数:定义域为凸集,两个点的线性组合的函数值小于两个点函数值的线性组合。
凸规划:凸函数在凸集上的优化。
梯度、二阶梯度:

单位向量:欧式长度为1.
方向导数:就是梯度与方向的内积
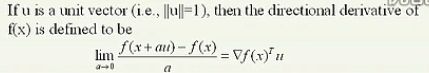
凸函数性质:
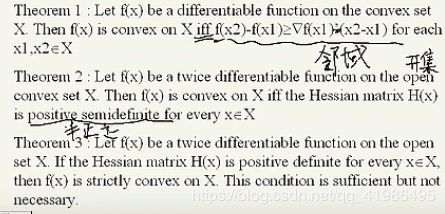
局部最小和全局最小:
1、目前算法只可以保证局部最小。想全局只有全部穷举。
2、凸函数局部最小即为全局最小。
3、随机优化算法可以以概率1找到全局最优解,但需要耗费时间。
===================================================
2 conditions for optimization
necessary condition for 普通函数局部最小
1、一阶梯度为0
2、二阶梯度大于0,半正定。
sufficient condition for 普通函数局部最小
1、一阶梯度为0,且二阶正定(严格大于0)。
奇异点
满足必要条件,但是不满足充分条件,仍为局部最小的点。
sufficient condition for 凸函数最小
1、一阶梯度等于0。
existence of optimal solutions
1、如果f(x)连续,且x是一个compact(closed and bounded),则最优解存在。
==============================================
3 one-dimension search technique
对于单峰函数
Dichotomous(二分法):二分法缩小搜索区间,迭代终止条件是区间长度小于给定值。
equal-interval search:等分区间进行缩小。
fibonacci search: 区间缩小的比例跟fibonacci数列有关系,本质也是缩小区间。不同之处在于先计算迭代次数,然后才迭代。
golden-section:新区间与老区间长度为0.618.
fibonacci与golden搜索计算效率较高,新点的计算数量少,fibonacci效率最高。
二次插值法:在极小值点附近,用二次三项式去逼近目标函数,然后求解最优值。(此方法精度低,速度快)
newton’s method:用于求方程的根,那么我们求最小值,即需要求的是导数的根。
x n + 1 = x n − H − 1 ( x n ) ∇ f ( x n ) x_{n+1}=x_{n}-H^{-1}(x_{n}) \nabla f(x_{n}) xn+1=xn−H−1(xn)∇f(xn)
===================================================
4 unconstrained gradient techniques
缺点:局部最优解
思想: 梯度计算—>方向+步长
=--------------------------------------------------------------------------------------
最速下降法:
方向为当前点的负梯度方向,
步长每一步选取最优步长 (一维最优化),
收敛性: 线性
缺点:
1、无法在有限步骤找到最优解,靠近最小值时收敛速度很慢。
2、锯齿形下降,效率不高。
m i n λ > = 0 f ( x + λ d ) min_{\lambda>=0 } f(\bf{x+\lambda d} ) minλ>=0f(x+λd)
=--------------------------------------------------------------------------------------
牛顿法:
迭代公式: x n + 1 = x n − H − 1 ( x n ) ∇ f ( x n ) x_{n+1}=x_{n}-H^{-1}(x_{n}) \nabla f(x_{n}) xn+1=xn−H−1(xn)∇f(xn)
方向: 海森阵的逆乘负梯度方向。
收敛性: 二阶收敛
优点: 二阶收敛,速度较快。
缺点: 需计算二阶梯度,计算复杂。
=-------------------------------------------------------------------------------------
拟牛顿法
基本思想是用不包含二阶导数的矩阵近似牛顿法中的海森矩阵。其余和牛顿方法一致,在一定条件下也是二阶收敛。
=-------------------------------------------------------------------------------------
信赖域方法
基本思想:大部分优化算法都是先定梯度方向,再确定步长。信赖域方法,先先取以 x k \bf x_k xk点为中心的球域,在此区域内优化目标函数的二次逼近式,直到满足精度。然后对此二次函数进行最优求解。
=-----------------------------------------------------------------------------------
最小二乘法
目标函数是若干各函数的平法和的形式,这种问题为最小二乘问题。
里面常用的方法为Gauss-newton法,LM法。
基本思想: 也是将函数用二次函数进行逼近,直接带入最小二乘形式进行分析。然后形式类似牛顿公式。
===================================================
5 quadratically convergent minimization algorithm
conjugate direction(共轭方向)
若两个向量满足如下关系,则说u与v相对于对称正定矩阵A共轭。
( u , A v = 0 ) (u,Av=0) (u,Av=0)
收敛性: 二次收敛
**方向:**第一次方向为最速下降方向,之后为共轭方向
**步长:**选取最优步长(一维最优化)。
缺点: 需要计算梯度
power算法可以不根据梯度构造共轭方向
=--------------------------------------------------------------------------------------
variable-mertic算法(变尺度)
方向: 一个迭代公式,方向是矩阵(想用Hassan阵,但是避免求梯度而采用迭代公式)乘梯度。
步长: 最优步长。
6 constraints and lagrange multipliers
可行解:满足所有约束条件的解
需要有约束的问题转换为无约束问题(代价是增加问题规模)。
等式约束
则利用拉个朗日乘子法
L ( x , λ ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) L(x,\lambda )=f(x)+\sum_{i=1}^{m}{\lambda_{i}g_{i}(x)} L(x,λ)=f(x)+i=1∑mλigi(x)
必要条件:

不等式约束
引入松弛变量 θ i \theta_i θi,将不等式约束转换为等式约束
L ( x , λ ) = f ( x ) + ∑ i = 1 m λ i ( h i ( x ) − θ i 2 ) L(x,\lambda )=f(x)+\sum_{i=1}^{m}{\lambda_{i}(h_{i}(x)-\theta_{i}^2)} L(x,λ)=f(x)+i=1∑mλi(hi(x)−θi2)
note:
若求解得到 λ i = 0 \lambda_i=0 λi=0则说明加入拉格朗日项后的最优解等于原问题的最优解,该约束的可行区域包含该最优解点。
7 optimization with inequality constraints
Kuhn-Tucker theorem(KT条件) :主要用于理论分析较多

kt条件的几何意义:
在约束极小点处,函数的负梯度方向一定可以表示为所有起作用约束在该点梯度的非负线性组合。
8 constrained gradient techniques
以下两种方法应该都从可行点出发。
hemstiching method
当前点在可行区域时,沿目标函数负梯度方向行走,
若违反某个约束,则沿该约束的梯度相关方向行走,直到进入可行区域,
缺点: 效率比较低
可行方向法
将有约束的非线性规划问题,转换为利用线性规划求解。

9 penalty function method
基本思想:有约束问题转换为无约束问题


缺点:不等式的惩罚函数法不可求导。
10 二次规划
二次规划是非线性规划中的特例。目标函数是二次函数,约束是线性约束。
lagrange方法
用途: 将具有等式约束的问题转换为无约束优化问题。
求解: 直接找梯度为0的点(尽管书上方程一堆,但也就是这个概念)。
active set方法
用途: 可以解决具有不等式线性约束的二次规划问题。
基本思想: 有效集方法就是将此问题转换为求解等式约束的问题。在每次迭代中,以已知的可行点为起点,把在该点起作用的约束作为等式约束,在此条件下极小化目标函数,其余约束暂且不管。求解到新的可行点后,重复上述做法。
个人理解: 根据当前可行点所在位置,首先确定有效集(起作用的等式约束),在此有效集上确定方向,最优步长(考虑最优步长时需考虑所有约束,防止下一个点跑到可行区域以外)。到了下一个点,重新确定有效集,重新开始优化。迭代终止的条件是通过判断此点是否是起作用约束的最优点(通过KT条件判断)。
本质: 个人理解,约束是线性的,寻找点是沿着边界进行寻找的。
