数据结构---线性表（结构体实现）

一、线性表的定义

线性表（Linear List）是具有相同特性的数据元素的一个有限序列

二、线性表的顺序存储结构——顺序表

元素类型：ElemType

每个元素占用存储空间大小（即字节数）：sizeof(ElemType)

整个线性表占用存储空间大小：n*sizeof(ElemType)。n表示线性表的长度。

C/C++中，用数组存放线性表中的元素及其逻辑关系

数组大小：MaxSize，一般定义为一个整型常量。语句为

#define MaxSize 50    //数值根据需要改变

第一个元素下标从0开始，最多共存放MaxSize个元素，下标范围为：0 ~ MaxSize-1 

定义一个data数组来存储线性表中的所有元素，并定义一个整型变量length来存储线性表的实际长度。语句为：

typedef int ElemType;    //自定义类型语句，定义整型常量ElemType

typedef struct{
    ElemType data[MaxSize];    //数据类型为ElemType的长度为MaxSize的data数组
    int length;        //记录线性表的实际长度，length < MaxSize时data数组中有空闲空间
}SqList;        //顺序表类型，类似于class中的类名，新定义的一个数据类型的名称

当线性表长度小于数组大小时，该数组中可能会有一部分空闲空间。 

建立顺序表

由数组元素a[0..n-1]创建顺序表L。将a中的每个元素依次放入顺序表中，并将n赋值给顺序表的长度域。算法为：

void CreateList(SqList * &L, ElemType a[], int n){
    int i=0, k=0;
    L = (SqList *)malloc(sizeof(SqList));    //分配存储线性表的空间
    while(idata[k] = a[i];
        k++; i++;
    }
    L->length = k;        //设置线性表的实际长度，设置为k（即a的长度n）
}

 补充malloc：分类存储空间，且字节数需要我们自己计算，并且最后要显式地强行转化为一个实际类型的指针。如：

int* p;

p = (int *)malloc(sizeof(int) * 128);

初始化线性表 InitList(&L) —— 时间复杂度为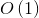

构造一个空的线性表，即分配线性表的内存空间（MaxSize* sizeof(ElemType)）并将length（线性表实际长度）设为0。算法为：

SqList* &L含义：L本身为一个SqList类型的指针，即SqList*，再&，即传入的是指针L的地址

void InitList(SqList* &L){
    L = (SqList *)malloc(sizeof(SqList));
    L->length = 0;
}

时间复杂度为，因为不存在遍历

销毁线性表 DestroyList&L) —— 时间复杂度为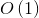

释放线性表L所占用的内存空间。当不再需要顺序表时，务必调用DestroyList函数释放其空间（系统会自动释放指针变量L，但不会自动释放L所指向的存储空间，可能造成内存泄漏）。

void DestroyList(SqList* &L){
    free(L);
}

判断线性表是否为空表 ListEmpty(L) —— 时间复杂度为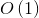

返回一个布尔值

bool ListEmpty(SqList* L){
    return L->length == 0;
}

求线性表的长度ListLength(L) —— 时间复杂度为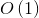

int ListLength(SqList* L){
    return (L->length);
}

输出线性表 DispList(L) —— 时间复杂度为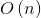 

时间复杂度为，因为需要遍历，存在for循环

void DistList(SqList* L){
    for(int i=0; ilength; i++)
        cout << L->data[i];
    cout << endl;
}

求线性表中某个数据元素值 GetElem(L, i) —— 时间复杂度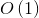 

i为要查找元素的索引值。返回i索引值处的元素值。算法为：

ElemType GetElem(SqList* L, int i){
    if(i >= 0 && i <= L->length-1)
        return L->data[i];
}

按元素值查找 LocateElem(L, e) —— 时间复杂度为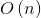

时间复杂度为，因为需要遍历。算法为：

int LocateElem(SqList* L, ElemType e){
    int i=0;
    while(ilength && L->data[i]!=e)
        i++;
    if(i>=L->length)    return 0;
    else 
        return i;    
}

插入数据元素 ListInsert(&L, i, e) —— 时间复杂度为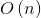

在索引值为i的位置上插入元素。插入成功返回true，否则返回false。

插入一个元素，后面的元素都要向后移，移动次数与插入位置和线性表长度有关，时间复杂度为。

bool ListInsert(SqList* &L, int i, ElemType e){
    if(i<0 && i>L->length && i>=MaxSize)
        return false;
    for(int j=L->length;j>i;j--)
        L->data[j] = L->data[j-1];        //从原来第i位开始，全部向后移一位
    L->data[i] = e;        //将插入的值填到第i位上
    L->length++;        //线性表长度加1
    return true;
}

删除数据元素 ListDelete(&L, i) —— 时间复杂度为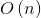

删除成功返回true，否则返回false。

时间复杂度为，理由同上。算法为：

bool ListDelete(SqList* &L, int i){
    if(i<0 || i>=L->length)
        return false;
    for(int j=i;jlength;j++)
        L->data[j] = L->data[j+1];
    L->length--;        //线性表实际长度减1
    return true;
}

三、顺序表的应用示例

Q1：假设一个线性表采用顺序表表示，设计一个算法，删除其中所有值为x的元素，要求算法时间复杂度为，空间复杂度为。

A1：

#include 
using namespace std;

#define MaxSize 20                //同上
typedef int ElemType;    
typedef struct{   
	ElemType data[MaxSize];    
	int length;       
}SqList;     

void CreateList(SqList * &L, ElemType a[], int n) {...} //同上
ElemType GetElem(SqList* L, int i) {...}
int LocateElem(SqList* L, ElemType e) {...}
bool ListDelete(SqList* &L, int i) {...}
void DistList(SqList* L) {...}
void DestroyList(SqList* &L) {...}

void DeleteCertainElem(ElemType a[], int n, ElemType delElem);    //新函数声明

int main() {
	int a[10] = { 1, 3, 5, 3, 7, 5, 7, 6, 8, 2 };
	DeleteCertainElem(a, 10, 5);
	system("pause");
}

void DeleteCertainElem(ElemType a[], int n, ElemType delElem) {
	int k = 0;
	SqList* L;
	CreateList(L, a, n);
	for (int i = 0; i < L->length; i++) {
		if (GetElem(L, i) == delElem)
			k++;
		else
			L->data[i - k] = L->data[i];
	}
	L->length -= k;
	DistList(L);
	DestroyList(L);
}

Q2：有一个顺序表L，假设元素类型ElemType为整型，设计一个尽可能高效的算法，将第一个元素作为基准，将所有小于等于它的元素移到该基准的前面，将所有大于它的元素移到该基准的后面。

Q3：有一个顺序表L，假设元素类型ElemType为整型，设计一个尽可能高效的算法，将所有奇数移到所有偶数的前面。

 

线性表的链式存储结构 —— 链表

链表（Linked List），每个存储结点不仅包含数据域，而且包含指针域（表示元素之间逻辑关系）。

在线性表的链式存储中，通常每个链表带有一个头结点

头指针（head pointer）：指向头结点的指针，唯一标识该链表。

首指针（first pointer）：指向首结点（或开始结点）的指针。

尾指针（tail pointer）：指向尾结点的指针。

从一个链表的头指针所指的头结点出发，沿着结点的链（即指针域的值）可以访问到每个结点。

线性表的存储密度高于链表的存储密度。

四、单链表（Singly Linked List）

每个结点中除保函数据以外，只设置一个指针域，用于指向其后继结点。

LinkNode：每个结点的数据类型

data：每个结点包括的存储元素的数据域

ElemType：数据域的类型

next：存储后继结点位置的指针域

LinkNode类型声明

typedef int ElemType;

typedef struct LNode{
    ElemType data;
    struct LNode* next;
}LinkNode;        //单链表结点类型

单链表中头结点的好处：

1   首结点的插入和删除操作与其他结点一致，无需进行特殊处理

2   无论单链表是否为空都有一个头结点，因此统一了空表与非空表的处理过程 

插入结点操作

 在单链表中数据域为a的结点（由指针p指向它）之后，插入一个数据域为x的结点（由s指向它）。

s->next = p->next;

p->next = s;

删除结点操作

删除单链表中数据域为a的结点（由p指向它）的后继结点。

p->next = p->next->next;

//一般情况下，还应释放删除结点的存储空间

q = p->next;

p->next = q->next;      //或 p->next = p->next->next;

free(q);

建立单链表 

1）头插法 —— 时间复杂度为

从一个空表开始一次读取数组a中的元素，生成一个新结点（由s指向它），将读取的元素存放到该结点的数据域中，然后将其插入到当前链表的表头上（即头结点之后），直到数组a读取完为止。

采用头插法建立的单链表中数据节点的顺序与数组a中元素的顺序相反。算法为：

void CreateListF(LinkNode* &L, ElemType a[], int n){
    LinkNode *s;
    L = (LinkNode *)malloc(sizeof(LinkNode));    //为头结点L分配结点内存
    L->next = NULL;
    for(int i=0;idata = a[i];            //并赋值
        s->next = L->next;            //插入头结点的后面
        L->next = s;
    }
}

 2）尾插法 —— 时间复杂度为

前部分同头插法，但是是将新结点插入当前链表的表尾上，因此需要增加一个尾指针r，使其始终指向当前链表的尾结点。

因此，每次插入一个新结点之后要让r指向这个新结点并将r所指结点的next域置为空。

采用尾插法建立的单链表中数据节点的顺序与数组a中元素的顺序相同。算法为：

void CreateListR(LinkNode* &L, ElemType a[], int n){
    LinkNode *s, *r;            //指向新结点的指针s，始终指向尾结点的指针r
    L = (LinkNode *)malloc(sizeof(LinkNode));
    r = L;
    for(int i=0;idata = a[i];
        r->next = s;
        r = s;
    }r->next = NULL;
}

初始化线性表 InitList(&L) —— 时间复杂度为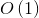

建立一个空的单链表，即创建一个头结点并将其next值设为空。算法为：

void InitList(LinkNode * &L){
    L = (LinkNode *)malloc(sizeof(LinkNode));
    L->next = NULL;
}

销毁线性表 DestroyList(&L) —— 时间复杂度为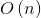

该运算释放单链表L占用的内存空间，即逐一释放全部节点的空间。过程：

让pre、p指向两个相邻结点（初始时pre指向头结点，p指向首结点）。当p不为空时循环，释放pre，然后pre、p同步后移一个结点。循环结束时，pre指向尾结点，然后再将其释放。算法为：

void DestroyList(LinkNode* &L){
    LinkNode *pre, *p;
    pre = L;
    p = L->next;
    while(p!=NULL){
        free(pre);
        pre = p;        //或 pre = pre->next;
        p = p->next;
    }
    free(pre);
}

判断线性表是否为空表 ListEmpty(L)  —— 时间复杂度为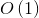

即判断头结点指针的next域是否为空。算法为：

bool ListEmpty(LinkNode *L){
    return L->next == NULL;
}

求线性表的长度 ListLength(L)  —— 时间复杂度为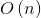

int ListLength(LinkNode *L){
    int n=0;
    LinkNode* p = L;    //设置一个指针，初始时指向头结点
    while(p->next!=L){
        n++;
        p = p->next;
    }
    return n;
}

输出线性表 DistList(L) —— 时间复杂度为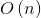

void DistList(LinkNode *L){
    LinkNode* p = L->next;
    while(p!=NULL){
        cout << p->data;
        p = p->next;
    }
    cout<

求线性表中某个数值元素值 GetElem(L, i, &e) —— 时间复杂度为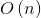

bool GetElem(LinkNode* L, int i, ElemType &e){    //传入一个已定义的ElemType类型的变量的引用
    LinkNode* p = L->next;
    if(i<=0) return false;    //无效传入值i
    while(jnext;
        j++;
    }
    if(p==NULL) return false;        //若i超出链表长度
    else{
        e = p->data;            //数据域赋值给e，e是传入的提前定义了的ElemType变量
        return true;
    }
}

按元素值查找LocateElem(L, e)  —— 时间复杂度为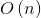

int LocateList(LinkNode* L, ElemType e){
    LinkNode* p = L->next;
    int k=0;
    while(p->data!=e && p!=NULL){
        k++;
        p = p->next;
    }
    if(p==NULL) return -1;
    else 
        return k;
}

插入数据元素 ListInsert(&L, i, e)  —— 时间复杂度为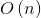

该算法先找到单链表L中的第i-1个结点，由p指向它。若存在这样的结点，则将数据域值为e的结点插入p所指的结点的后面。算法为：

bool ListInsert(LinkNode * &L, int i, ElemType e){
    int j=0;
    if(i<0) return false;
    LinkNode *p = L, *s;        //指向第i-1个结点的指针p，指向新插入结点的指针s
    while(p!=NULL && jnext;
    }
    if(p==NULL) return false;
    else{                        //找到第i-1个结点后，创建新结点及指针s
        s = (LinkNode *)malloc(sizeof(LinkNode));       //给新结点分配内存空间 
        s->data = e;            //设置新结点的数据域的值
        s->next = p->next;
        p->next = s;
        return true;
    }
}

删除数据元素 ListDelete(&L, i, &e) —— 时间复杂度为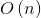

方法同上。算法为：

bool ListDelete(LinkNode * &L, int i, ElemType &e){
    int j = 0;
    if(i<0) return false;
    LinkNode* p = L;
    while(p->next!=NULL&jnext;
    }
    if(p==NULL) return false;    //不存在第i-1个结点
    else{
        if(p->next==NULL) return false;        //不存在第i个结点
        e = p->next->data;
        p->next = p->next->next;
        free(p->next);
        return true;
    }
}

 五、单链表的应用示例

Q1：有一个带头结点的单链表，设计一个算法将其拆分成两个带头结点的链表、，按a、b来分，要求使用的头结点。

Q2：设计一个算法，删除一个单链表L中元素值最大的结点（假设这样的结点唯一）。

Q3：有一个带头结点的单链表L（至少有一个数据结点），设计一个算法使其元素有序递增排列。

六、双链表

在双链表中，每个结点既包括一个指向后继结点的指针，又包含一个指向前驱结点的指针。

DLinkNode类型声明

typedef struct DNode{
    ElemType data;
    struct DNode *prior;
    struct DNode *next;
}DLinkNode;            //双链表结点类型DLinkNode

建立双链表

1）头插法

void CreateListF(DLinkNode * &L, ElemType a[], int n){
    L = (DLinkNode *)malloc(sizeof(DLinkNode));
    DLinkNode *s;
    L->prior = NULL;
    L->next = NULL;
    for(int i=0;idata = a[i];
        s->next = L->next;    //或 s->next = NULL;
        if(L->next!=NULL)
            L->next->prior = s;
        s->prior = L;
        L->next = s;
    }
}

2）尾插法

void CreateListR(DLinkNode * &L, ElemType a[], int n){
    DLinkNode *s, *r;        //新结点的指针s和始终指向尾结点的指针r
    L = (DLinkNode *)malloc(sizeof(DLinkNode));
    L->prior = L->next = NULL;
    r = L;                //初始时尾结点即为头结点，设置r初始值
    for(int i=0;idata = a[i];
        r->next = s;
        s->prior = r;
        r = s;
    }r->next = NULL;
}

对双链表进行操作时，要注意需要更改4个指针的值，2*prior和2*next

双链表的应用示例

Q1：有一个带头结点的双链表L，设计一个算法将其所有元素逆置。

Q2：有一个带头结点的双链表L（至少有一个数据结点），设计一个算法使其元素递增有序排列。

八、循环链表

循环链表（Circular Linked List），循环单链表数据类型与循环双链表数据类型分别为LinkNode和DLinkNode，与非..相同。

非循环单链表改为循环单链表：将尾结点的next指针域由原来的空改为指向头结点。因此，从表中任一点出发（单链表向后）都能找到链表中的其他结点。

非循环双链表改为循环双链表：将尾结点的next指针域由原来的空改为指向头结点，将头结点的prior指针域由原来的空改为指向尾结点。

各操作对应算法基本相同，主要区别：

1   对于循环单(双)链表，判断表尾结点p的条件是p->next == L;

2   在循环双链表L中，可以通过L->prior快速找到尾结点

循环链表的应用示例

Q1：有一个带头结点的循环单链表L，设计一个算法统计其data域值为x的结点个数。

Q2： 有一个带头结点的循环双链表L，设计一个算法删除第一个data域值为x的结点。

Q3：设计一个算法，判断带头结点的循环双链表L（含两个以上结点）中的数据结点是否对称。

九、有序表

有序表（Ordered List）可以采用线性表（类型为SqList）和链表（单链表结点类型为LinkNode，双链表结点类型为DLinkNode）进行存储。

1）以顺序表（线性表）存储

除ListInsert()算法与前面有差异，其余都相同。有序顺序表的ListInsert()算法为：

void ListInsert(SqList * &L, ElemType e){
    int i=0, j;
    while(iLength && L->data[i]Length-1;j>=i;j--)
        L->data[j+1] = L->data[j];
    L->data[i] = e;
    L->Length++;
}

2）以单链表存储

除ListInsert()算法与前面有差异，其余都相同。有序单链表的ListInsert()算法为：

void ListInsert(LinkNode * &L, ElemType e){
    LinkNode *s, *p;    //新结点指针s以及插入位置的前驱结点指针p
    p = L;
    while(p->next!=NULL && p->next->datanext;        //找到插入结点的前驱结点，由指针p指向它
    s = (LinkNode *)malloc(sizeof(LinkNode));
    s->data = e;
    s->next = p->next;
    p->next = s;
}

有序表的归并算法

问：假设有两个有序表LA和LB，设计一个算法，将他们合并成一个有序表LC（假设不存在重复的元素），要求不破坏原有表LA和LB。

完整代码：

方法一）线性表

#include 
using namespace std;
#define MaxSize 50

typedef int ElemType;
typedef struct {
	ElemType data[MaxSize];
	int length;
}SqList;

void CreateList(SqList * &L, ElemType a[], int n) {        //同上
	int i = 0, k = 0;
	L = (SqList *)malloc(sizeof(SqList));    
	while (idata[k] = a[i];
		k++; i++;
	}
	L->length = k;        
}

void InitList(SqList* &L) {                        //同上
	L = (SqList *)malloc(sizeof(SqList));
	L->length = 0;
}

void DistList(SqList* L) {                        //同上
	for (int i = 0; ilength; i++)
		cout << L->data[i]<<"   ";
	cout << endl;
}

ElemType GetElem(SqList* L, int i) {            //同上
	if (i >= 0 && i <= L->length - 1)
		return L->data[i];
}

void ListAppend(SqList* L, ElemType e) {            //新添函数，往List末尾append
	if (L->length < MaxSize) {
		L->data[L->length] = e;
		L->length++;
	}
}

void UnionList(SqList * LA, SqList * LB, SqList * LC);            //新加函数的声明

int main() {
	int a1[8] = { 12,45,46,78,79,160,200,300 };
	int a2[11] = { 4,6,13,81,120,161,181,230,241,330,340 };
	SqList *LA, *LB, *LC;
	CreateList(LA, a1, 8);
	CreateList(LB, a2, 11);
	InitList(LC);

	UnionList(LA, LB, LC);
	DistList(LC);

	system("pause");
}

void UnionList(SqList * LA, SqList * LB, SqList * LC) {            //新定义函数定义
		int i_a = 0, i_b = 0, i_c = 0;
		while (i_a < LA->length && i_b < LB->length) {
			ElemType appendElem = LA->data[i_a] < LB->data[i_b]
				? LA->data[i_a] : LB->data[i_b];
			if (LA->data[i_a] < LB->data[i_b]) i_a++;
			else
				i_b++;
			ListAppend(LC, appendElem);
		}
		if (i_a == LA->length) {
			for (; i_b < LB->length; i_b++)
				ListAppend(LC, LB->data[i_b]);
		}
		else if (i_b == LB->length) {
			for (; i_a < LA->length; i_a++)
				ListAppend(LC, LA->data[i_a]);
		}	
}

方法二）单链表

#include 
using namespace std;

typedef int ElemType;
typedef struct LNode {
	ElemType data;
	struct LNode* next=NULL;
}LinkNode;

void CreateListR(LinkNode* &L, ElemType a[], int n) {                //同上
	LinkNode *s, *r;
	L = (LinkNode *)malloc(sizeof(LinkNode));
	r = L;
	for (int i = 0; idata = a[i];
		r->next = s;
		r = s;
	}r->next = NULL;
}

void InitList(LinkNode * &L) {                            //同上
	L = (LinkNode *)malloc(sizeof(LinkNode));
	L->next = NULL;
}

void DistList(LinkNode *L) {                            //同上
	LinkNode* p = L->next;
	while (p != NULL) {
		cout << p->data<<"   ";
		p = p->next;
	}
	cout << endl;
}

void UnionList(LinkNode *& LA, LinkNode *& LB, LinkNode *& LC);            //新填函数声明

int main() {
	int a1[5] = { 10,12,57,85,120};
	int a2[3] = { 13,81,121};
	LinkNode *LA, *LB, *LC;
	CreateListR(LA, a1, 5); 
	CreateListR(LB, a2, 3);
	InitList(LC);

	UnionList(LA, LB, LC);
	DistList(LC);

	system("pause");
}

void UnionList(LinkNode *& LA, LinkNode *& LB, LinkNode *& LC) {                //新填函数定义
	LinkNode *p_a, *p_b, *r;				        //LC的尾结点
	p_a = LA->next, p_b = LB->next, r = LC;
	while (p_a != NULL && p_b != NULL) {
		if (p_a->data < p_b->data) {
			r->next = p_a;
			r = p_a;
			p_a = p_a->next;
		}
		else if (p_a->data > p_b->data) {
			r->next = p_b;
			r = p_b;
			p_b = p_b->next;
		}
	}
	if (p_a == NULL) {
		while (p_b != NULL) {
			r->next = p_b;
			r = p_b;
			p_b = p_b->next;
		}
	}
	else if (p_b == NULL) {
		while (p_a != NULL) {
			r->next = p_a;
			r = p_a;
			p_a = p_a->next;
		}
	}
}

 有序表的应用

Q1：已知3个带头结点的单链表LA、LB和LC中的结点均依元素值递增排列（假设每个链表中不存在数据值相同的结点，单不同链表中可能存在），设计一个算法对LA链表进行如下操作：是操作后的链表LA中仅留下3个表中均包含的数据元素的结点，且没有数据值相同的节点，并释放LA中所有无用结点。要求算法的时间复杂度为O(m+n+p)，其中m、n、p分别为4个表的长度。

Q2：已知一个有序单链表L（允许出现值域重复的结点），设计一个高效算法删除值域重复的结点，并分析算法的时间复杂度。

Q3：一个长度为n（n>=1）的升序序列S，处在第n/2个位置的数称为S的中位数。例如，若序列S1 = (11, 13, 15, 17, 19)，则S1的中位数为15两个数列的中位数是它们所有元素的升序序列的中位数。现有两个等长的升序序列A和B，设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列A和B的中位数。假设升序序列采用顺序表存储。