求最大公约数的4种算法(C++)
求最大公约数的4种算法(C++)
一、实验目的
1.计算两个正整数的最大公约数和最小公倍数,并进行程序的调式与测试。
2.理解四种不同的求最大公约数的方法,学习其思维模式。
3.了解算法的概念。对问题的分析时,进行合适的算法设计。
二、算法设计
1.题目分析
(1)首先输入一对正整数,对两个数进行判断,若不是正整数,则给出提示并重新输入,直至两个数均为正整数为止。
(2)将两个数传入计算最大公约数的函数和计算最小公倍数的函数中,求解输出。
(3)验证各种算法的效率,在求解函数之前设置一个计时器开始运行,在函数执行完毕后,结束计时,计算出两个时间节点的差,即可得出每个函数执行一定次数的时间。规定统一的次数,将每种算法所用时间进行对比即可。
2.算法设计
1.辗转相除法,又称欧几里得算法。用于计算两个正整数a,b的最大公约数和最小公倍数,其依赖于gcd(a,b) = a (b=0)和gcd(b,a mod b) (b!=0).
2.穷举法,也叫枚举法,求最大公约数时从两者中较小的数开始,由大到小列举,直到找到第一个公约数为止。
3.更相减损法,若两个正整数都为偶数,则用2约简,直到不能约简为止。然后用大数减小数,将差与较小的数比较,再以大数减小数,直到减数和差相等为止。
4. Stein算法,两个数均为偶数时有公约数2,且公约数一定为偶数。一个奇数一个偶数时,因为其奇偶性的不同,所以其最大公约数一定为奇数。当两个数均为奇数时,其最大公约数一定是奇数。
三、业务流程图设计
欧几里得算法:
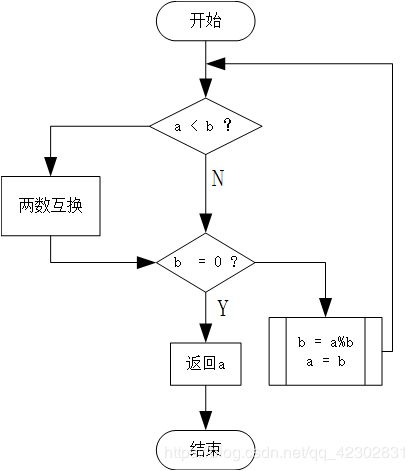
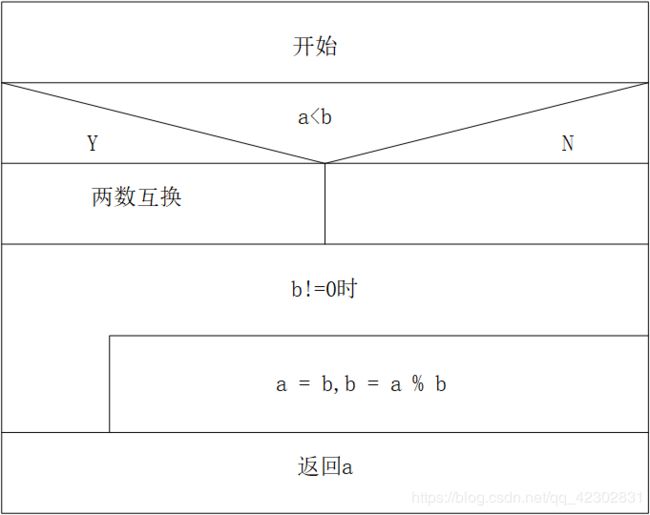
穷举法:
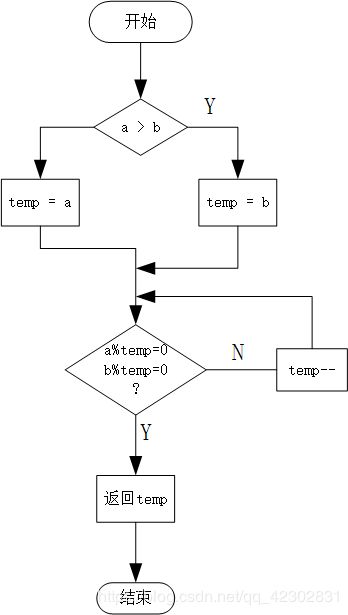
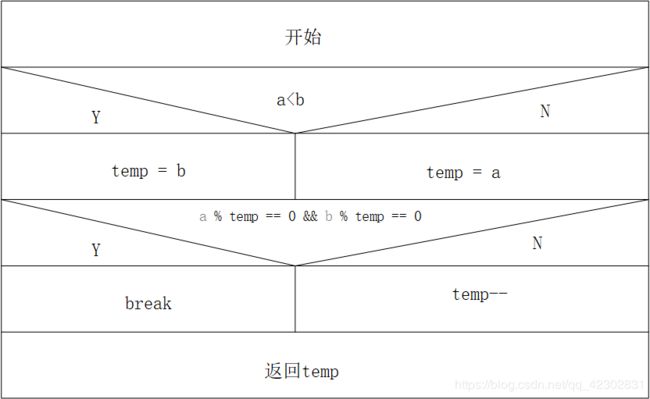
更相减损法:
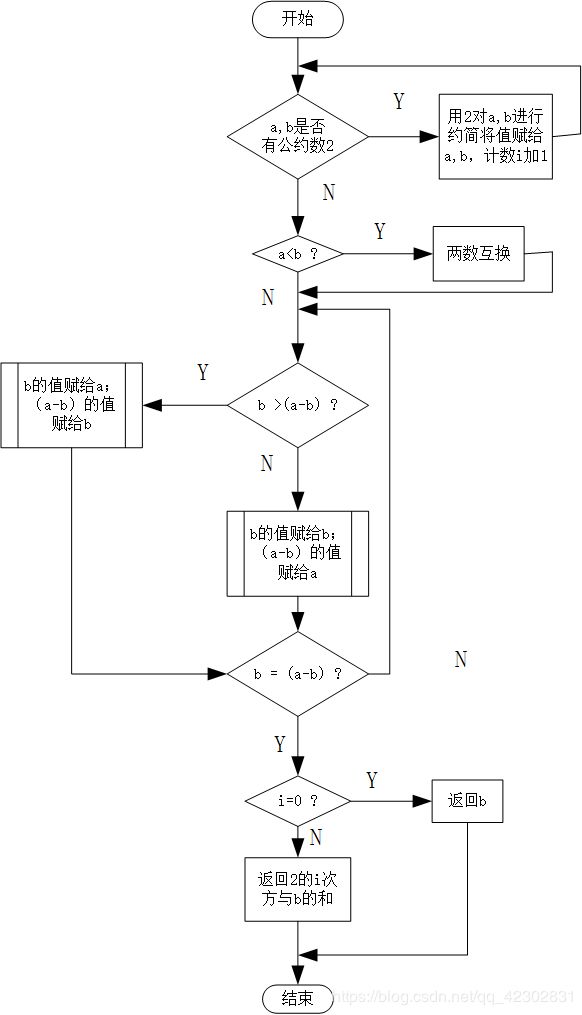

Stein算法:
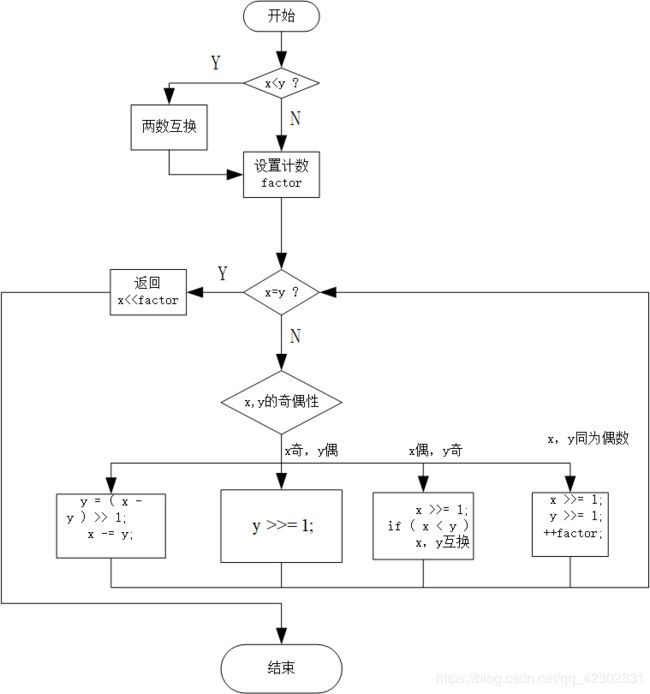

四、主要代码(2.0.0版)
/*********************************************************************************
*FileName: Test1.cpp
*Author: Qixiang.Su
*e-mail: [email protected]
*Version: 2.0.0
*Date: 2019.3.10
*Description: 求两个正整数的最大公约数和最小公倍数
* 理解各种算法求解过程
*History:
1.Date: 2019.3.10
Author: Elf.苏洛曦
Modification: Create project
2.Date: 2019.3.12
Author: Elf.苏洛曦
Modification: 1.0.0版
3.Date: 2019.3.14
Author: Elf.苏洛曦
Modification: 2.0.0版
**********************************************************************************/
#include五、调试和测试
1.在1.0.0版本中
一次进行测试,出现了错误,如下图:
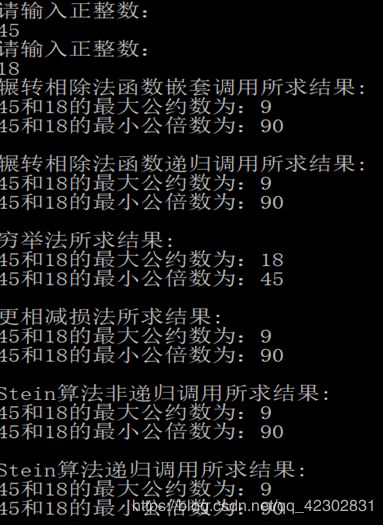
在编译时没有错误,在运行过程也无错误,在结果中,穷举法的结果与其他的不同。对穷举法进行单独测试,结果如下:

与实际不符,结果也是错误的,通过逐语句调试

发现求最大公约数中temp的值存在异常,通过仔细检查,将while(temp > 0)写成了while(temp = 0),嵌套出现了层次错误。改正后,运行结果如下:

最大公约数正确,最小公倍数错误,对求最小公倍数的函数进行逐语句后
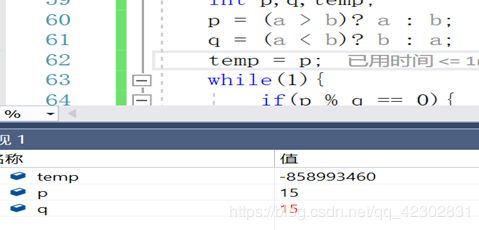
p和q的值相同,存在错误,仔细检查后发现将(a>b)写成了(a
2. 2.0.0版本
在2.0.0版本中取消了1.0.0版本中的输入要求数的对数,增加了对一组数据想要循环次数的输入,这样免去了测试时手动输入多组数据的程序。
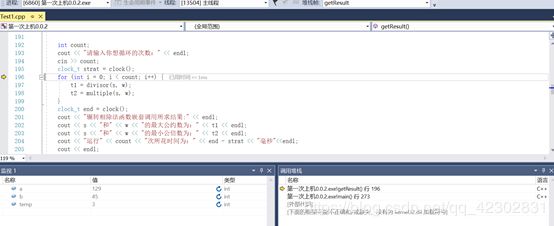
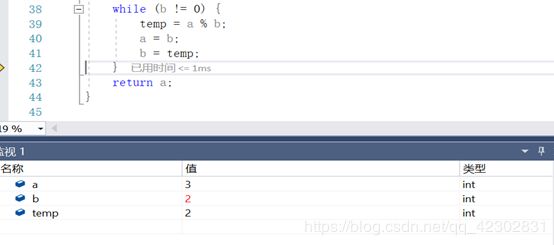
通过监视,查看各个变量的变化情况,如下图:
(1) 输入两个正整数15和9,执行求解代码100000次,比较各种算法的速度,结果如下图:
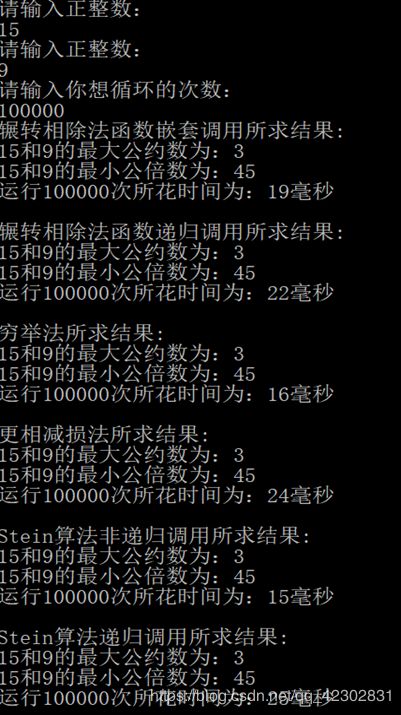
从结果可以看出Stein算法非递归比较快,数字较小时,穷举法所用时间也比较短。
(2)输入两个正整数143和345,执行求解代码100000次,比较各种算法的速度,结果如下图:
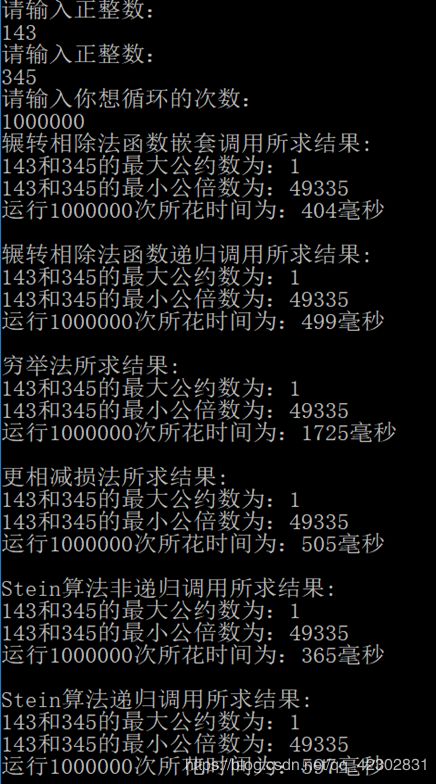
在数字较大时且函数循环次数较多之后,Stein算法的执行速度还是很快,而穷举法需要的时间大幅度增长,其他几种算法的时间相差不大。
(3)输入两个正整数12和8,执行求解代码100000次,比较各种算法的速度,结果如下图:

数字较小时,穷举法的优势还是很明显,执行速度优于其他几种算法。
同时通过上面的几组测试发现,非递归的速度要优于递归。
六、总结
通过本次实验,学习到了求最大公约数几种常见的算法,对算法也有了一定的认识。也领略到了算法的思维的精妙之处。在上机过程中也出现了一些错误,通过逐步调试也解决了问题。在程序上,还存在一些缺陷,在进行速度的测试时,仅用一组数据的循环次数来判断,这种情况下,就忽略了手动输入数据时数据的复杂性。在输入正整数时仅对数字的正负性进行了判断,而对于其他会出现异常的情况,如在输入数字时误输入字母、符号等,未进行处理。没有通过正则表达式来判断输入,也未将异常进行捕捉和抛出。所以要学习的设计方法还有很多,只有学习到更多的处理方法,才能让自己的程序更具健壮性。