OpenGL学习之旅（三）——Bezier曲线理论与OpenGL实现

Bezier曲线理论与OpenGL实现

在专栏的第二节中，我简单梳理了计算机图形学当中简单的数理知识和常见的图形学概念。考虑到后期的具体项目——曲面造型，我准备抽出几节特意学习和整理了一下经常用到的样条曲线、曲面的理论知识和实现，今天写个博客来整理一下Bezier曲线的理论以及代码实现。

01样条曲线、曲面概念
在绘图术语中，**样条是通过一组指定点集而生成平滑曲线的柔性带。**当绘制曲线时，几个较小
的加权沿着样条的长度分配并固定在绘图表上的相应位置。术语——样条曲线(spline curve )原指
使用这种方式绘制的曲线。
数学上使用分段三次多项式函数来描述这种曲线，其中各曲线段的连接
处有连续的一次和二次导数。
在计算机图形学中，
样条曲线指由多项式曲线段连接而成的曲线，在每段的边界处满足特定的连续性条件。
样条曲面(spline surface)可以使用两组正交样条曲线进行
描述。
如果我们用丄表示控制点的位置，则样条曲面上的任意一点可用样条曲线很合函数的积来计算：

02 Bezier曲线概念

Bezier样条逼近方法是法国工程师Hem Bezier为雷诺(Renault)公司设计汽车车身而开发的。
Bezier曲线通过控制曲线上的四个点（起始点、终止点以及两个相互分离的中间点）来创造、编辑图形。其中起重要作用的是位于曲线中央的控制线。这条线是虚拟的，中间与贝塞尔曲线交叉，两端是控制端点。移动两端的端点时贝塞尔曲线改变曲线的曲率（弯曲的程度）；移动中间点（也就是移动虚拟的控制线）时，贝塞尔曲线在起始点和终止点锁定的情况下做均匀移动。
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次Bezier曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。

尽管有的图形软件将Bezier样条曲线控制点数限定为4,但一般来说，Bezier样条曲线段可以拟合任何数目的控制点。Bezier多项式的次数取决于曲线将逼近的控制点数量及相关位置。
多数情况下Bezier曲线是一个阶数比控制点数少1的多项式：三点生成一个抛物线，四点生成一个三次曲线，依次类推。
而在一定安排的控制点控制下，可获得退化的Bezier多项式。例如，使用三个共线控制点生成的Bezier曲线是一直线段。
而所有控制点都在同一坐标位置时生成的说Bezier曲线”是一个点。

02 Bezier曲线描述

对于一般不加约束的Bezier曲线，混合函数描述是最方便的表示办法。
假设给出n+1个控制点位置：

这里k可以取0到n，这些坐标点将混合产生下列位置向向量P(u),用来描述P0和pn间逼近Bezier多项式函数的路径：

Bezier混合函数是Bernstein多项式:
这里，参数C（n，k）是二项式系数：
由此推导获得单个曲线坐标三个参数方程的集合：

对于多项式形式，Bezier曲线的一般表达式为：

其中，三次Bezier样条曲线表达式

03 Bezier曲线性质

1、端点性质：

a）P(0)=P0, P(1)=Pn, 即：曲线过二端点。

b）P’(0)=n(P1-P0), P’(1)=n(Pn-Pn-1)

即：在二端点与控制多边形相切。

2、凸包性：Bezier曲线完成落在控制多边形的凸包内。

3、对称性：由Pi与Pn-i组成的曲线，位置一致，方向相反。

4、包络性：Pn (t)=(1-t)Pn-1 (t)+tPn-1 (t)

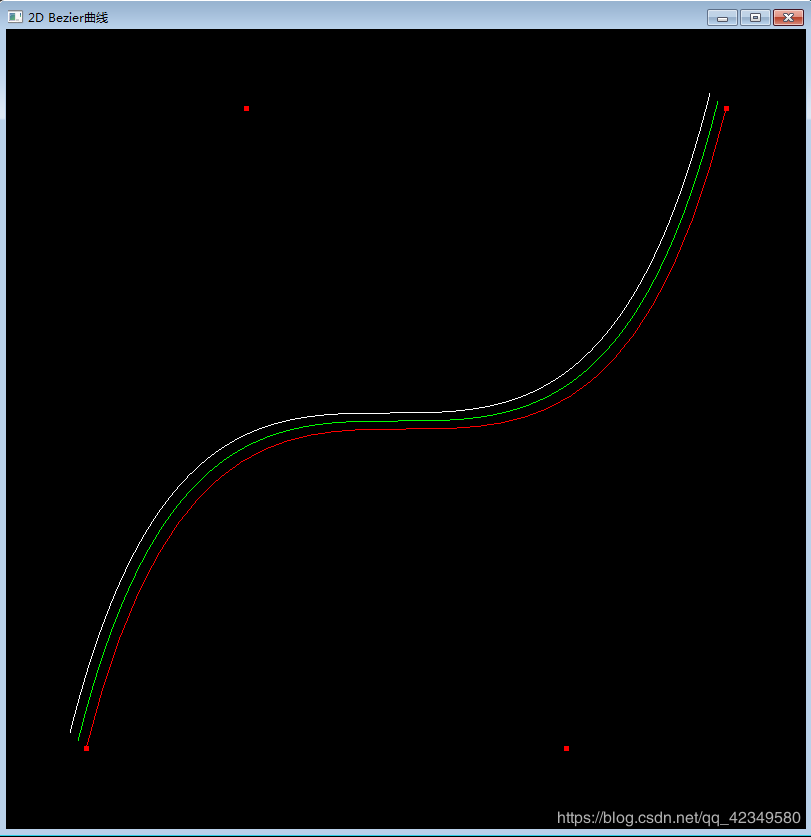
04 Bezier曲线的OpenGL实现
参考CSDN博主麦田IT

#include "stdafx.h"
#include 
#include 
#include 
 
//4个控制点的3D坐标——z坐标全为0
GLfloat ctrlpoints[4][3] = {
    { -4, -4, 0 }, { -2, 4, 0 }, { 2, -4, 0 }, { 4, 4, 0 }
};
 
void init(void)
{
    //背景色
    glClearColor(0.0, 0.0, 0.0, 1.0);
    //将控制点坐标映射为曲线坐标
    //参数1：GL_MAP1_VERTEX_3，3维点坐标
    //参数2和3：控制参数t或u的取值范围[0, 1]
    //参数4：曲线内插值点间的步长3————3维坐标
    //参数5：曲线间的补偿为顶点数4个————总步长为12
    //参数6：控制点二维数组首元素地址
    //注意: 若是在这里设置了相关参数，后续对ctrlpoints内容更改曲线不变
    glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
    //打开开关——允许3维坐标控制点到参数点转换开关
    glEnable(GL_MAP1_VERTEX_3);
    glShadeModel(GL_FLAT);
 
    //代码开关2：去掉本注释，可启用反走样
    /*
    glEnable(GL_BLEND);
    glEnable(GL_LINE_SMOOTH);  //允许直线反走样
    glHint(GL_LINE_SMOOTH_HINT, GL_FASTEST);  // Antialias the lines
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
    */
}
 
void display(void)
{
    int i;
    glClear(GL_COLOR_BUFFER_BIT);
    glColor3f(1.0, 1.0, 1.0);
 
    //代码开关1：去掉本注释，查看动态的曲线绘图效果：动态更新控制点坐标
    /*
    for(int t = 0; t < 4; t++) {
    for(int j = 0; j < 3; j++)
    ctrlpoints[t][j] = (rand() % 1024 / 1024.0 - 0.5) * 10;
    }
    //动态映射
    glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
    */
    glLoadIdentity();
    glColor3f(1.0, 0.0, 0.0);
    //绘制连续线段
    glBegin(GL_LINE_STRIP);
    //参数t或u取值为i/30，共计31个点
    for (i = 0; i <= 30; i++)
        glEvalCoord1f((GLfloat)i / 30.0);   //根据4个控制点坐标的参数化插值
    glEnd();
    /* 显示控制点 */
    glPointSize(5.0);
    glBegin(GL_POINTS);
    for (i = 0; i < 4; i++)
        glVertex3fv(&ctrlpoints[i][0]);
    glEnd();
 
    glTranslatef(-0.1f, 0.1f, 0.0f);
    glColor3f(0.0, 1.0, 0.0);
    //glLineWidth(2.0);
    //绘制连续线段——线段数越多，曲线越光滑
    glBegin(GL_LINE_STRIP);
    //设置参数t或u取值为i/60，共计61个点
    //实验：若让t从-2变化到+2，可看到什么效果
    for (i = 0; i <= 60; i++)
        glEvalCoord1f((GLfloat)i / 60.0);  //根据4个控制点坐标的参数化插值
    glEnd();
 
    glTranslatef(-0.1f, 0.1f, 0.0f);
    glColor3f(1.0, 1.0, 1.0);
    //绘制连续线段
    glBegin(GL_LINE_STRIP);
    //设置参数t或u取值为i/60，共计61个点
    //实验：若让t从-2变化到+2，可看到什么效果
    for (i = 0; i <= 100; i++)
        glEvalCoord1f((GLfloat)i / 100.0);
    glEnd();
 
    glutSwapBuffers();
}
 
//3D空间中绘制2D效果，采用正交投影
void reshape(GLsizei w, GLsizei h)
{
    glViewport(0, 0, w, h);
 
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    if (w <= h)
        glOrtho(-5.0, 5.0, -5.0*(GLfloat)h / (GLfloat)w, 5.0*(GLfloat)h / (GLfloat)w, -5.0, 5.0);
    else
        glOrtho(-5.0*(GLfloat)w / (GLfloat)h, 5.0*(GLfloat)w / (GLfloat)h, -5.0, 5.0, -5.0, 5.0);
 
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();
}
 
void keyboard(unsigned char key, int x, int y)
{
    switch (key)
    {
    case 'x':
    case 'X':
    case 27:   //ESC键
        exit(0);
        break;
    default:
        break;
    }
}
 
int main(int argc, char** argv)
{
    srand((unsigned int)time(0));
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);//使用双缓存模式和深度缓存
    glutInitWindowSize(800, 800);
    glutInitWindowPosition(0, 0);
    glutCreateWindow("2D Bezier曲线");
    init();
    glutDisplayFunc(display);
    glutReshapeFunc(reshape);
    glutKeyboardFunc(keyboard);
    glutIdleFunc(display);//设置空闲时调用的函数
    glutMainLoop();
    return 0;
}

运行结果

代码我还没撸明白，我想在三次B样条曲线再抠实现细节。晚安。