python之K-NN算法实现(鸢尾花数据)
运行环境:Jupyter
一、K-近邻算法
K-近邻(K-NN)算法可以说是最简单的机器算法。构建模型只需要保存训练数据集即可。想要对新数据点做出预测,算法会在训练数据集中找到最近的数据点,也就是它的“最近邻”。
这里实现的是一个监督学习中的分类(二分类)问题。我们需要预测出测试数据的所属类别。
二、实现步骤
1.获取数据集
导入Numpy方便操作数据,pyplot用来绘图
解释:
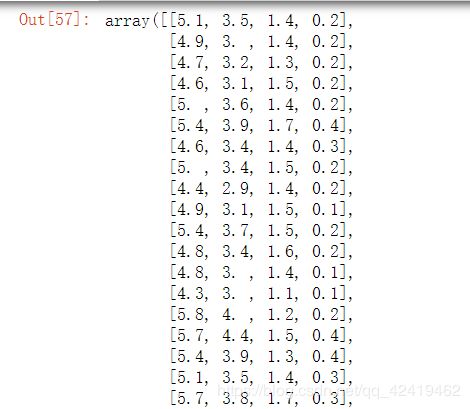
(1)load_iris():导入鸢尾花数据
(2)x_data = datas[‘data’][0:150],y_data= datas[‘target’][0:150]:
利用切片操作获取数据集。‘data’对应的就是鸢尾花的数据。target对应的是类别。
…一共150组数据
y_data(代表类别):

也是150组数据。
2.将数据集分为训练集和测试集
训练集获取:

解释:利用切片操作将源数据的一半作为训练集。从0开始到150,左闭右开,步长为2。获取75组数据。
测试集数据获取:

解释:利用切片操作将源数据的一半作为训练集。从1开始到150,左闭右开,步长为2。获取75组数据。
3.构建模型
1.绘制散点图:

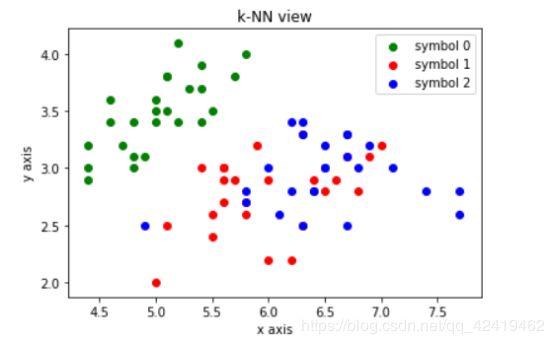
注意:这里的横纵坐标分别对应鸢尾花的花萼的长和宽,由于四维向量不能绘制,所以取前两个元素作为说明。
2.k-NN的过程:

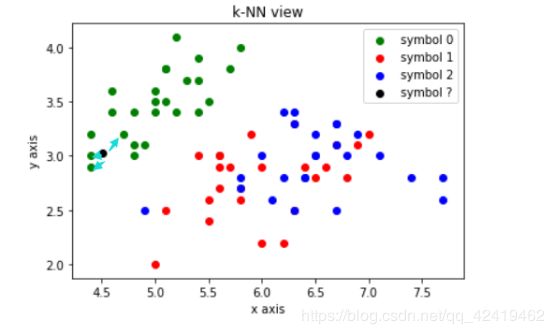
解释:黑色的点表示需要预测的数据,我们需要求出离它最近的几个点的类别,利用投票法决定黑色点的类别,由图可知黑色点最后的类别应该和绿色点一样为0
具体算法:(求距离就是求两坐标点间的距离) 
最后结果预测是0和绿色点的类别相同至此构建模型结束。
4.用测试集的数据测试求出精度

解释:这里其实就是对测试集数据重复之前的操作,然后将测试集数据的预测结果和其正确的类别进行比较,记录预测正确的个数,最后除以总共测试的数据就求出了此模型的精度。

三、算法实现
?代码是顺序的
from sklearn.datasets import load_iris
import numpy as np
import matplotlib.pyplot as plt
#加载鸢尾花数据
datas = load_iris()
#利用切片收集150组鸢尾花数据(datas['data']表示datas的‘data’key值对应的数据,即鸢尾花的花瓣花萼数据)
x_data = datas['data'][0:150]
#表示鸢尾花源数据的类别,0代表setosa,1代表versicolor,2代表virginica(K-NN算法处理基于监督学习的分类问题)
#datas['target']表示datas的‘target’key值对应的数据,即鸢尾花的类别(标签)
y_data = datas['target'][0:150]
#产生训练集(鸢尾花源数据的百分之50)
x_train = x_data[0:150:2]
y_train = y_data[0:150:2]
#产生测试集(鸢尾花源数据的百分之50)
x_test = x_data[1:150:2]
y_test = y_data[1:150:2]
y_data
#绘制训练集(这里只以鸢尾花数据的前两个作为坐标绘制借来说明算法的原理,因为四维的不能绘制)
plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1],color='g',label="symbol 0")
plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1],color='r',label="symbol 1")
plt.scatter(x_train[y_train==2,0],x_train[y_train==2,1],color='b',label="symbol 2")
plt.title("k-NN view")
plt.xlabel("x axis")
plt.ylabel("y axis")
plt.legend()
plt.show()
#新增加一个数据(该数据是示例)判断其的类别为0 or 1 or 2(根据距离)
x = np.array([4.5023242,3.03123123,1.3023123,0.102123123])
plt.scatter(x_train[y_train==0,0],x_train[y_train==0,1],color='g',label="symbol 0")
plt.scatter(x_train[y_train==1,0],x_train[y_train==1,1],color='r',label="symbol 1")
plt.scatter(x_train[y_train==2,0],x_train[y_train==2,1],color='b',label="symbol 2")
plt.scatter(x[0],x[1],color='black',label="symbol ?")
plt.title("k-NN view")
plt.xlabel("x axis")
plt.ylabel("y axis")
plt.legend()
plt.show()
#K-NN过程(计算距离,并将其存储到列表)
from math import sqrt
distances = []
for x0 in x_train:
d = sqrt(np.sum((x-x0)**2))
distances.append(d)
#将距离排序(由大到小)返回的是元素下标
near = np.argsort(distances)
k = 3
#选择出前5个最近元素的类别
topK_y = [y_train[i] for i in near[:k]]
topK_y
from collections import Counter
#统计元素出现的个数(即代表这鸢尾花类别的数字的个数)
votes = Counter(topK_y)
votes
#找出票数最多的一个元素,该方法返回的是一个元组,我们只需要key值(也就是类别)
#出预测的结果,0代表setosa,1代表versicolor,2代表virginica
result = votes.most_common(1)[0][0]
result
#注意这里用的是上面的数据,但是步骤是重新开始的因为要一个个遍历测试集并将预测结果与源数据中的结果比较得出正确率
#统计测试数据的精度
count = 0
index = 0
for j in x_test:
distance = []
x = j;
#计算距离
for x1 in x_train:
t = sqrt(np.sum((x-x1)**2))
distance.append(t)
near = np.argsort(distance)
topK_y = [y_train[i] for i in near[:k]]
votes = Counter(topK_y)
result = votes.most_common(1)[0][0]
if y_test[index]==result:
count=count+1
index=index+1
else:
index=index+1
score=count/75
score
若代码有误请参考:代码