数据挖掘十大算法(一):k-近邻算法
1、基本概念
k近邻法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一种基本分类与回归方法。它的工作原理是:存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
1.计算已知类别数据集中的点与当前点之间的距离;
2.按照距离递增次序排序;
3.选取与当前点距离最小的k个点;
4.确定前k个点所在类别的出现频率;
5.返回前k个点所出现频率最高的类别作为当前点的预测分类。
2、约会网站配对效果判定
海伦女士一直使用在线约会网站寻找适合自己的约会对象。尽管约会网站会推荐不同的任选,但她并不是喜欢每一个人。
经过一番总结,她发现自己交往过的人可以进行如下分类:
不喜欢的人
魅力一般的人
极具魅力的人
海伦收集的样本数据主要包含以下3种特征:(按照顺序)
1. 每年获得的飞行常客里程数
2. 玩视频游戏所消耗时间百分比
3. 每周消费的冰淇淋公升数
label:1代表不喜欢,2代表魅力一般,3代表极具魅力
导入模块
import numpy as np
import operator
import os
import pandas as pd
读入数据
# 这里采用最先进的读数据方式~比传统的处理方法好太多
def read_file(filename):
# '\t' 指按照空格切分
data = pd.read_csv(filename, header=None, sep='\t')
ret = pd.DataFrame(data)
feature_mat = ret.values[:, 0:3]
label_mat = ret.values[:, 3]
return feature_mat, label_mat
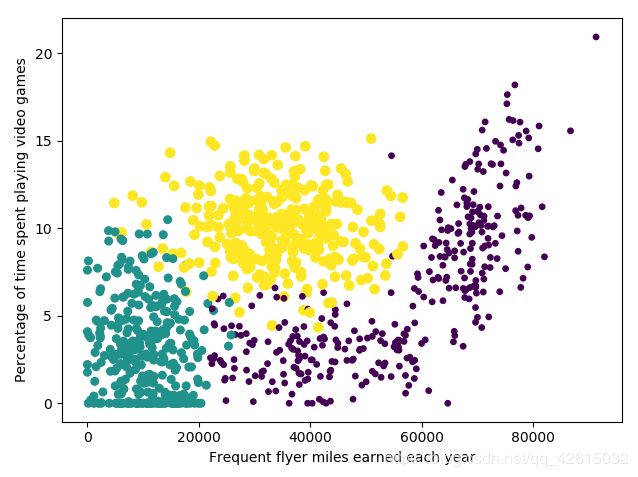
数据可视化
mydata, labels = read_file('datingTestSet2.txt')
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(mydata[:, 0], mydata[:, 1], 15.0*np.array(labels), 15.0*np.array(labels))
ax.set_xlabel('Frequent flyer miles earned each year')
ax.set_ylabel('Percentage of time spent playing video games')
plt.show()
# 可以明确看到两个特征之间的关系, 这时候我们完全可以排除别的特征!
# 重点把握np.tile函数的使用
# 归一化之后再次可视化 验证是否正确
def normal_data(data_mat):
m = data_mat.shape[0]
max_value = data_mat.max(axis=0)
min_value = data_mat.min(axis=0)
ranges = max_value - min_value
data_mat = (data_mat - np.tile(min_value, (m, 1))) / np.tile(ranges, (m, 1))
return data_mat, ranges, min_value
def class_dataset(test_data, train_data, train_label, k):
dataSetSize = len(train_data)
# 在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
test_mat = np.tile(test_data, (dataSetSize, 1))
distance = ((test_mat - train_data) ** 2).sum(axis=1)
distance = distance ** 0.5
index_distance = distance.argsort()
class_dic = {}
for i in range(k):
data_label = train_label[index_distance[i]]
class_dic[data_label] = class_dic.get(data_label, 0) + 1
class_dic = sorted(class_dic.items(), key=operator.itemgetter(1), reverse=True)
return class_dic[0][0]
def class_test():
ratio = 0.10
training_data, train_label = read_file('datingTestSet1.txt')
train_data, ranges, min_value = normal_data(training_data)
num_train = train_data.shape[0]
num_test = int(ratio * num_train)
error_count = 0
for i in range(num_test):
class_result = class_dataset(train_data[i, :], train_data[num_test:, :],
train_label[num_test:], 3)
print('''The classifier came back with: {}, the real answer is :{}'''
.format(class_result, train_label[i]))
if class_result == train_label[i]:
pass
else:
error_count = error_count + 1
print('The total error rate is %2f' % (error_count / float(num_test)))
The classifier came back with: 2.0, the real answer is :3.0
The classifier came back with: 1.0, the real answer is :1.0
The classifier came back with: 2.0, the real answer is :2.0
The classifier came back with: 1.0, the real answer is :1.0
The classifier came back with: 3.0, the real answer is :3.0
The classifier came back with: 3.0, the real answer is :3.0
The classifier came back with: 2.0, the real answer is :2.0
The classifier came back with: 1.0, the real answer is :1.0
The classifier came back with: 3.0, the real answer is :1.0
The total error rate is 0.050000
最后使用算法:构建完整可用系统
import numpy as np
import operator
import os
import pandas as pd
def class_dataset(test_data, train_data, train_label, k):
dataSetSize = len(train_data)
# 在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
test_mat = np.tile(test_data, (dataSetSize, 1))
distance = ((test_mat - train_data) ** 2).sum(axis=1)
distance = distance ** 0.5
index_distance = distance.argsort()
class_dic = {}
for i in range(k):
data_label = train_label[index_distance[i]]
class_dic[data_label] = class_dic.get(data_label, 0) + 1
class_dic = sorted(class_dic.items(), key=operator.itemgetter(1), reverse=True)
return class_dic[0][0]
def read_file(filename):
# '\t' 指按照空格切分
data = pd.read_csv(filename, header=None, sep='\t')
ret = pd.DataFrame(data)
feature_mat = ret.values[:, 0:3]
label_mat = ret.values[:, 3]
return feature_mat, label_mat
def normal_data(data_mat):
m = data_mat.shape[0]
max_value = data_mat.max(axis=0)
min_value = data_mat.min(axis=0)
ranges = max_value - min_value
data_mat = (data_mat - np.tile(min_value, (m, 1))) / np.tile(ranges, (m, 1))
return data_mat, ranges, min_value
def class_person():
'''
误点:
:return:
'''
class_dic = {1: '你一点也不喜欢这个人~',
2: '你可能会有一点喜欢这个人~',
3: '你会真的很喜欢这个人!'}
train_data, train_label = read_file('datingTestSet2.txt')
train_data, ranges, min_vale = normal_data(train_data)
fly = float(input('请输入每年获得的飞行常客里程数:'))
game_time = float(input('请输入每天玩视频游戏所消耗时间百分比:'))
ice_cream = float(input('请输入每周消费的冰淇淋公斤数:'))
test_data = np.array([fly, game_time, ice_cream])
# 一定不要忘了对输入的测试数据也有进行归一化处理
test_data = (test_data - min_vale) / ranges
ret = class_dataset(test_data, train_data, train_label, 3)
return '系统提示:你对该名男子的感觉是:{}'.format(class_dic[ret])
if __name__ == '__main__':
ret = class_person()
print(ret)
3、约会网站配对之sklearn再实现
Scikit learn 也简称sklearn,是机器学习领域当中最知名的python模块之一。sklearn包含了很多机器学习的方式:
Classification 分类
Regression 回归
Clustering 非监督分类
Dimensionality reduction 数据降维
Model Selection 模型选择
Preprocessing 数据与处理
使用sklearn可以很方便地让我们实现一个机器学习算法。一个复杂度算法的实现,使用sklearn可能只需要调用几行API即可。所以学习sklearn,可以有效减少我们特定任务的实现周期。
KNneighborsClassifier参数说明:
1. n_neighbors:默认为5,就是k-NN的k的值,选取最近的k个点。
2. weights:默认是uniform,参数可以是uniform、distance,也可以是用户自己定义的函数。uniform是均等的权重,
就说所有的邻近点的权重都是相等的。distance是不均等的权重,距离近的点比距离远的点的影响大。用户自定义的函数,接收距离的数组,
返回一组维数相同的权重。
3. algorithm:快速k近邻搜索算法,默认参数为auto,可以理解为算法自己决定合适的搜索算法。除此之外,用户也可以自己指定搜索算法
ball_tree、kd_tree、brute方法进行搜索,brute是蛮力搜索,也就是线性扫描,当训练集很大时,计算非常耗时。
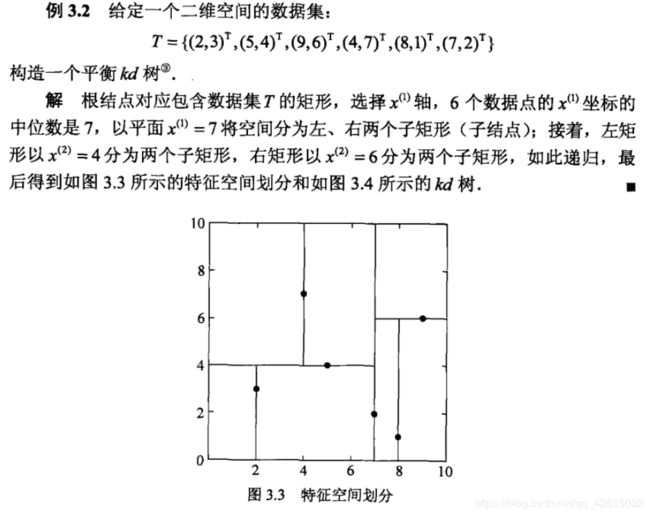
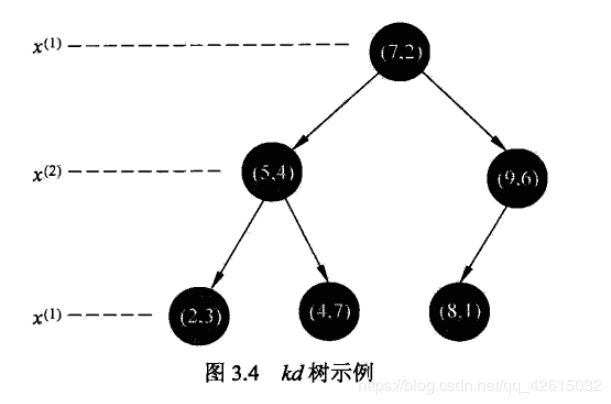
kd_tree,构造kd树存储数据以便对其进行快速检索的树形数据结构,kd树也就是数据结构中的二叉树。以中值切分构造的树,
每个结点是一个超矩形,在维数小于20时效率高。ball tree是为了克服kd树高纬失效而发明的,
其构造过程是以质心C和半径r分割样本空间,每个节点是一个超球体。
4. leaf_size:默认是30,这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度,
同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。
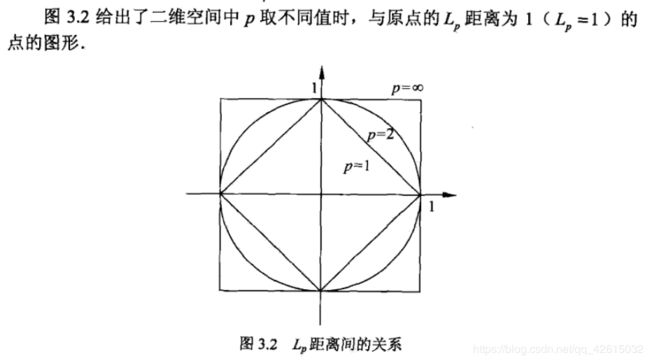
5. metric:用于距离度量,默认度量是minkowski,也就是p=2的欧氏距离(欧几里德度量)。
6. p:距离度量公式。在上小结,我们使用欧氏距离公式进行距离度量。除此之外,还有其他的度量方法,例如曼哈顿距离。
这个参数默认为2,也就是默认使用欧式距离公式进行距离度量。也可以设置为1,使用曼哈顿距离公式进行距离度量。
7. metric_params:距离公式的其他关键参数,这个可以不管,使用默认的None即可。
8. n_jobs:并行处理设置。默认为1,临近点搜索并行工作数。如果为-1,那么CPU的所有cores都用于并行工作。
KNeighborsClassifier提供了以一些方法供我们使用,如图所示

import numpy as np
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
def read_file(filename):
# '\t' 指按照空格切分
data = pd.read_csv(filename, header=None, sep='\t')
ret = pd.DataFrame(data)
feature_mat = ret.values[:, 0:3]
label_mat = ret.values[:, 3]
return feature_mat, label_mat
def normal_data(data_mat):
m = data_mat.shape[0]
max_value = data_mat.max(axis=0)
min_value = data_mat.min(axis=0)
ranges = max_value - min_value
data_mat = (data_mat - np.tile(min_value, (m, 1))) / np.tile(ranges, (m, 1))
return data_mat, ranges, min_value
def class_test():
training_data, train_label = read_file('datingTestSet1.txt')
test_data, test_label = read_file('datingTestSet2.txt')
train_data, ranges, min_value = normal_data(training_data)
test_data, test_ranges, test_min_value = normal_data(test_data)
num_test = len(test_data)
error_count = 0
## 建立模型
model = KNeighborsClassifier(n_neighbors=3, algorithm='auto')
## 拟合模型
model.fit(train_data, train_label)
for i in range(num_test):
class_result = model.predict(test_data[i].reshape(1, -1))
print('''The classifier came back with: {}, the real answer is :{}'''
.format(class_result, test_label[i]))
if class_result == test_label[i]:
pass
else:
error_count = error_count + 1
print('The total error rate is %2f' % (error_count / float(num_test)))
if __name__ == '__main__':
ret = class_person()
print(ret)
4、sklearn之breast cancer实现
重点把握:
可视化中拟合曲线的画法
测试集传入的方式, 可以一次性传入多个测试样本
知识点补充:
1.np.linspace 在指定的间隔内返回均匀间隔的数字
2.np.meshgrid 函数
根据传入的两个一维数组参数生成两个数组元素的列表。
如果第一个参数是xarray,维度是xdimesion,
第二个参数是yarray,维度是ydimesion。
那么生成的第一个二维数组是以xarray为行,共ydimesion行的向量;
而第二个二维数组是以yarray的转置为列,共xdimesion列的向量。
3.ravel() 为扁平化函数
x = np.arange(16).reshape(4, 4)
print(x.ravel())
输出:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]
4. np.r_:(row,行)将切片对象转换为沿第一轴的连接
np.c_:(column,列)将切片对象转换为沿第二轴的连接
5. 当前的图表和子图可以使用plt.gcf()和plt.gca()获得,分别表示Get Current Figure和Get Current Axes。在pyplot模块中,
许多函数都是对当前的Figure或Axes对象进行处理,比如说:plt.plot()实际上会通过plt.gca()获得当前的Axes对象ax,
然后再调用ax.plot()方法实现真正的绘图。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
# This is used for our dataset
from sklearn.datasets import load_breast_cancer
# =============================================================================
# We are using sklearn datasets to create the set of data points about breast cancer
# Data is the set data points
# target is the classification of those data points.
# The data[:, x:n] gets two features for the data given.
# If you want to get a different two features you can replace 0:2 with 1:3, 2:4,... 28:30,
# There are 30 features in the set so it can only go up to 30.
# If we wanted to plot a 3 dimensional plot then the difference between x and n needs to be 3 instead of two
# =============================================================================
dataCancer = load_breast_cancer()
data = dataCancer.data[:, 0:2]
target = dataCancer.target
# 模型建立和拟合
model = KNeighborsClassifier(n_neighbors=9, algorithm='auto')
model.fit(data, target)
# plots the points
plt.scatter(data[:, 0], data[:, 1], c=target, s=30, cmap=plt.cm.prism)
# Creates the axis bounds for the grid
axis = plt.gca()
x_limit = axis.get_xlim()
y_limit = axis.get_ylim()
# Creates a grid to evaluate model
x = np.linspace(x_limit[0], x_limit[1])
y = np.linspace(y_limit[0], y_limit[1])
X, Y = np.meshgrid(x, y)
xy = np.c_[X.ravel(), Y.ravel()] # (2500,2)
# Creates the line that will separate the data
boundary = model.predict(xy)
boundary = boundary.reshape(X.shape) # (50, 50)
# Plot the decision boundary
# plt.contour()是用来画等高线的. 通过boundary中的边界在X和Y中找到相应的坐标.打印出来一看便知
axis.contour(X, Y, boundary, colors='k')
# Shows the graph
plt.show()
5、算法提升
k k k近邻法三要素:距离度量、 k k k值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的pL距离。 k k k值小时, k k k近邻模型更复杂; k k k值大时, k k k近邻模型更简单。 k k k值的选择反映了对近似误差与估计误差之间的权衡,通常由交叉验证选择最优的 k k k。

K值的选择:
如果K值小,则模型复杂.估计误差增大
如果K值大,则模型简单.近似误差增大
6、总结
优点
简单好用,容易理解,精度高,理论成熟,既可以用来做分类也可以用来做回归
可用于数值型数据和离散型数据
训练时间复杂度为O(n);无数据输入假定
对异常值不敏感
缺点
计算复杂性高;空间复杂性高
样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少)
一般数值很大的时候不用这个,计算量太大。但是单个样本又不能太少,否则容易发生误分
最大的缺点是无法给出数据的内在含义