图像线性与非线性变换

变换目标

1、分段线性变换各种情况的变换效果对比
2、对数、指数变换、取反等多种非线性变换的效果对比

变换结果与分析

分段线性变换
1）变换函数

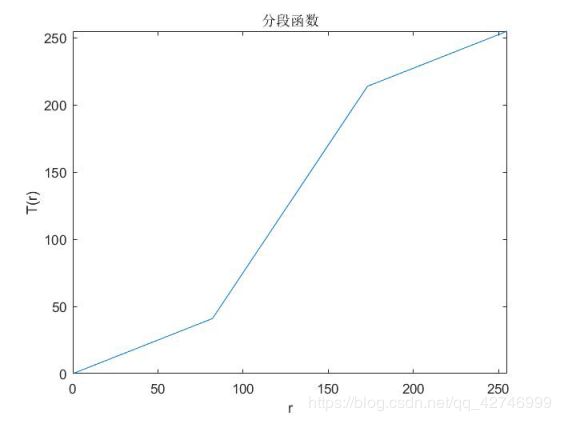
2）分段线性变换结果

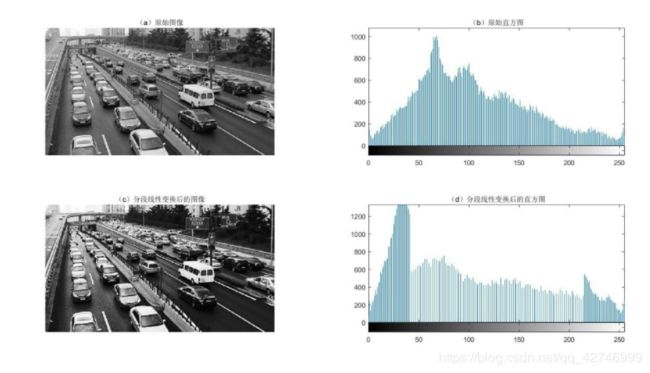
3）分段线性变换对比分析
通过变换，将灰度值小于82的变小，将灰度值大于173的增大，处于82与173之间的被拉伸。
对数变换
1）变换函数

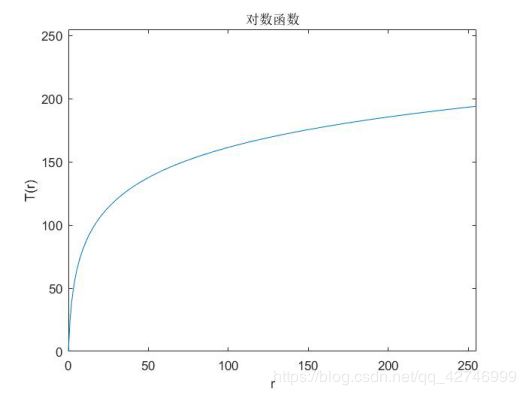
2）对数变换结果

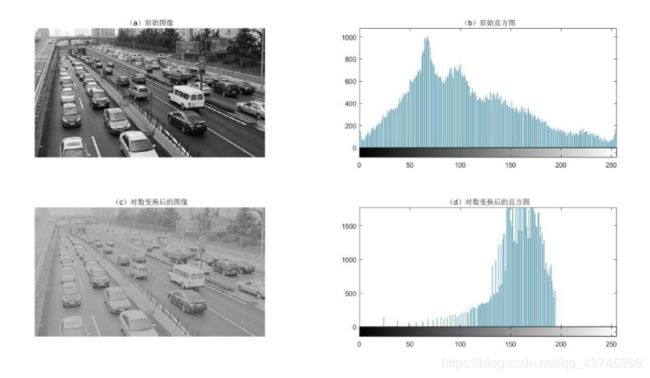
3）对数变换分析
低灰度值区域被拉伸，高灰度值区域被缩小，常数c越大，图像灰度值越集中于255，常数c越接近0，图像灰度值越接近于0.
指数变换
1）变换函数

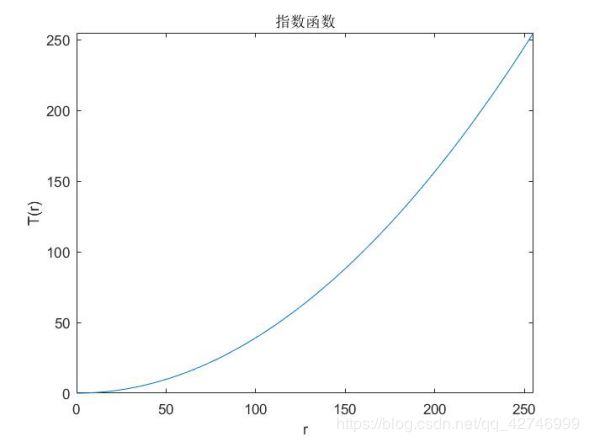
2）指数变换结果

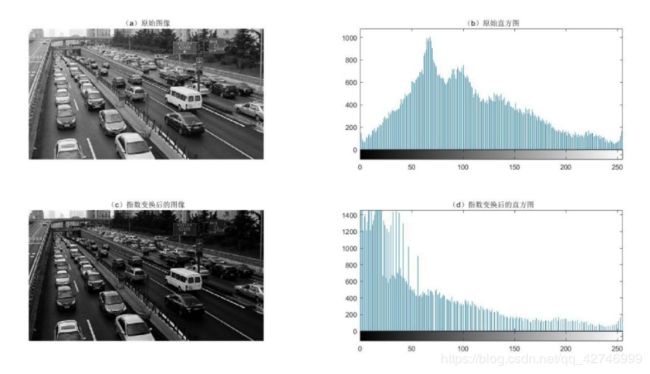
3）指数变换分析：
当指数大于1，图像灰度值减小，当指数小于1大于0，回想灰度值增大。
取反变换
1）取反变换函数

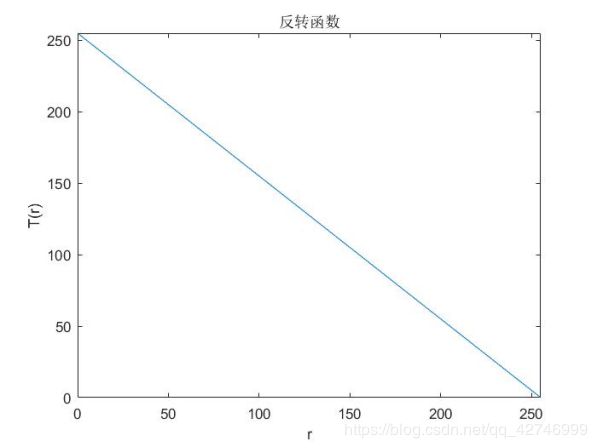
2）取反变换结果

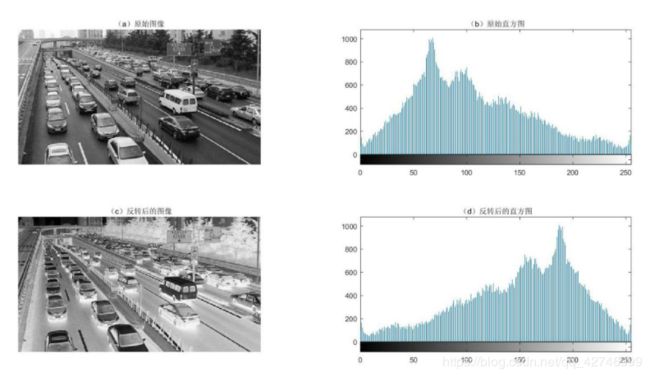
3）取反变换对比分析
增强了图像暗色区域中的白色或灰色细节，特别是黑色面积在尺寸上占主导地位的时候，效果逐渐明显。

代码

分段线性变换

%Write  by 长安 Rjex
%分段线性变换各种情况的变换效果对比
%name为图像文件名，(r1,s1),(r2,s2)为变换点
function B = pielinear(name,r1,s1,r2,s2)I = imread(name); 
if r1>r2||s1>s2
   error(message('MATLAB:pieLinear:invalidCoordinate'))
end 
A=rgb2gray(I);B = A; %确定分段函数方程
syms k b;
[k1,b1] =solve([k*r1+b==s1, 0*k+b==0], k,b);
[k2,b2] =solve([k*r2+b==s2, k*r1+b==s1], [k,b]);
[k3,b3] =solve([k*r2+b==s2, k*255+b==255], [k,b]); %符号变量转换成数值常量
k1 = double(k1);
k2 = double(k2);
k3 = double(k3);
b1 = double(b1);
b2 = double(b2);b3 = double(b3); %分段线性变换
for i = 1 : size(A,1)
    for j = 1 : size(A,2)    
        if A(i,j)<=r1       
             B(i,j) = double(A(i,j))*k1+b1; %此处须将A浮点化，否则对A的算术运算范围为0~255        
        elseif 
             A(i,j)>r1&&A(i,j)<=r2            
             B(i,j) = double(A(i,j))*k2+b2;        
         else            
             B(i,j) = double(A(i,j))*k3+b3;        
         end    
     end
end %原图与对比度拉伸后的图像

figure(1);
subplot(2,2,1),imshow(A),title('（a）原始图像');
subplot(2,2,2),imhist(A),title('（b）原始直方图');
subplot(2,2,3),imshow(B),title('（c）分段线性变换后的图像');
subplot(2,2,4),imhist(B),title('（d）分段线性变换后的直方图'); %分段函数的表示

figure(2);
x=0:1:255;y=(k1*x+b1).*(x>=0&x<=r1)+(k2*x+b2).*(x>r1&x<=r2)+(k3*x+b3).*(x>r2&x<=255);plot(x,y);axis([0 255 0 255]),title('分段函数'),xlabel('r'),ylabel('T(r)'); 

反转（取反）变换

%Write  by 长安 Rjex
%图像反转的变换效果对比%name为图像文件名
function B = negatrans(name)I = imread(name);
A=rgb2gray(I);
B = A; %图像反转
for i = 1 : size(A,1)
    for j = 1 : size(A,2)      
          B(i,j) = 255-double(A(i,j));
           %此处须将A浮点化，否则对A的算术运算范围为0~255    
    end
end %原图与图像反转后的图像

figure(1);
subplot(2,2,1),imshow(A),title('（a）原始图像');
subplot(2,2,2),imhist(A),title('（b）原始直方图');
subplot(2,2,3),imshow(B),title('（c）反转后的图像');
subplot(2,2,4),imhist(B),title('（d）反转后的直方图'); %反转函数的表示

figure(2);
x=0:1:255;y=255-x;plot(x,y),axis([0 255 0 255]),title('反转函数'),xlabel('r'),ylabel('T(r)'); 

对数变换

%Write  by 长安 Rjex
%对数变换各种情况的变换效果对比%name为图像文件名，c为对数变换中的常数，即：clog(r+1)
function B = logtrans(name,c)I = imread(name); 
A=rgb2gray(I);B = A; %对数变换
for i = 1 : size(A,1)
    for j = 1 : size(A,2)       
         B(i,j) = c*log(double(A(i,j))+1); %此处须将A浮点化，否则对A的算术运算范围为0~255    
    end
end %原图与对数变换后的图像

figure(1);
subplot(2,2,1),imshow(A),title('（a）原始图像');
subplot(2,2,2),imhist(A),title('（b）原始直方图');
subplot(2,2,3),imshow(B),title('（c）对数变换后的图像');
subplot(2,2,4),imhist(B),title('（d）对数变换后的直方图'); %对数函数的表示

figure(2);
x=0:1:255;y=c*log(x+1);plot(x,y);axis([0 255 0 255]),title('对数函数'),xlabel('r'),ylabel('T(r)'); 

指数变换

%Write  by 长安 Rjex
%指数变换各种情况的变换效果对比%name为图像文件名
function B = indextrans(name,c,r)
I = imread(name); 
A=rgb2gray(I);B = A; %指数变换
for i = 1 : size(A,1)
    for j = 1 : size(A,2)       
         B(i,j) = (double(A(i,j))^r.*c)/(255^r)*255; %此处须将A浮点化，否则对A的算术运算范围为0~255    
    end
end %原图与指数变换后的图像

figure(1);
subplot(2,2,1),imshow(A),title('（a）原始图像');
subplot(2,2,2),imhist(A),title('（b）原始直方图');
subplot(2,2,3),imshow(B),title('（c）指数变换后的图像');
subplot(2,2,4),imhist(B),title('（d）指数变换后的直方图'); %指数函数的表示

figure(2);
x=0:1:255;y=(x.^r.*c)/(255^r)*255;plot(x,y);axis([0 255 0 255]),title('指数函数'),xlabel('r'),ylabel('T(r)');