kesci文本情感分类练习赛
kesci文本情感分类练习赛(朴素贝叶斯)
原网址:https://www.kesci.com/home/competition/5c77ab9c1ce0af002b55af86/content/0
因为练习赛已经截止了,虽然提供了训练集和测试集,但是找不到答案。
他的数据集是名为「Roman Urdu DataSet」的公开数据集,所以我直接把这个数据集扒了下来,
从里面扣了9000条作为训练集,2000条作测试集,附于文末。
代码我是参考了这位大佬的博文,然后做了一些小的修改:
https://blog.csdn.net/sinat_34263473/article/details/89059912?tdsourcetag=s_pcqq_aiomsg
大的思路上面已经讲的很清楚了,代码我也附在文末,这里我说一下我觉得比较有价值的几个点:
朴素贝叶斯及数学推导
先来看一下朴素贝叶斯的公式;
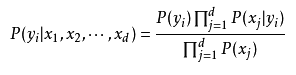
概率论里有这样一个知识:
P(XY)=P(X|Y)P(Y)
即:事件X和事件Y同时发生的概率=事件Y发生的概率*事件Y发生的情况下事件X发生的概率
所以就可以做出如下推导:
P(XY)=P(YX)=P(X|Y)P(Y)=P(Y|X)P(X),
所以就可以得出:
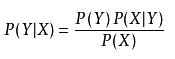
在这道题里X就是出现了哪些单词,Y就是句子是Positive还是Negative。
又因为句子中出现哪些单词相互独立,所以假设单词为x1,x2,x3…
P(X)=p(x1)p(x2)…*p(xn)
就有了最上面的式子。
其中p(yi)就是句子是y(Positive/Negative)的概率,
p(xj|yi)就是在句子是y(Positive/Negative)的情况下出现单词xj的概率,
记录在下面程序的p0Vect和p1Vect中。
朴素贝叶斯的优化
我们知道加法是比减法快的,而取对数可以把乘法化为加法,
又因为自然对数函数ln单调递增,所以p(y0)和p(y1)的大小关系在取对数后不变。
两边取对数,得:
Log(P(yi|x1,x2,…,xd))=Log(P(yi))+∑Log(P(xj|yi))-∑Log(P(xj))
代到题目里面,就是说:
p0’=Log(P(y0|x1,x2,…,xd))=Log(P(y0))+∑Log(P(xj|y0))-∑Log(P(xj))
p1’=Log(P(y1|x1,x2,…,xd))=Log(P(y1))+∑Log(P(xj|y1))-∑Log(P(xj))
由于最后是做预测,肯定是比较p0’和p1’谁大,即句子是Negative还是Positive的概率大,就预测结果是0还是1,观察到两个式子的最后都有一个减项-∑Log(P(xj));因为是要比大小,又因为a-c>b-c则a>b,所以最后一项可以在求概率的时候去掉,节省了大量的计算。
概率向量的处理
主要是这一段:
# 训练二分类朴素贝叶斯,返回3个参数
# p0Vect表示在类别0中,各个词汇出现的概率向量
# p1Vect表示在类别1中,各个词汇出现的概率向量
# pAbusive表示训练集中,类别1的概率
# trainMatrix表示训练集的词汇矩阵,是一组向量,trainMatrix[i]是一个向量
# trainCategory表示各个样本的类别
def trainNB0(trainMatrix, trainCategory):
numTrainDocs = len(trainMatrix)
numWords = trainMatrix.shape[1]
# 二分类问题,可直接对类别向量进行求和,即类别1的个数
pAbusive = sum(trainCategory) / numTrainDocs
p0Num = np.ones(numWords).reshape(1, -1)
p1Num = np.ones(numWords).reshape(1, -1)
# 为避免计算概率时,分母为0,
p0Denom = 2.
p1Denom = 2.
#下面的都是向量加法,每个词相加,加出来是向量
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
# 将频率转换成概率
p1Vect =np.log(p1Num / p1Denom)
p0Vect =np.log(p0Num / p0Denom)
print("Positive数据占比:",pAbusive)
return p0Vect, p1Vect, pAbusive
p0Vect, p1Vect, pAbusive = trainNB0(train_mat[:, :-1], train_mat[:, -1])
之前我们把每个句子的词向量统计出来了,所谓词向量就是对于一个句子,其中出现的单词置1,没出现的单词置0.这里用的是向量加法,是不同向量间相同位置的元素相加,所以所有的句子加出来就是这样一个向量:[count(word1),count(word2),count(word3),…,count(wordn)]
用这个向量除以总的单词出现的个数sum(trainMatrix[i]),就是每个词的概率向量,即:
[p(x1),p(x2),p(x3),…,p(xn)]
又因为可以对数优化,再用numpy.log求个对数,方便后面朴素贝叶斯的优化计算。
预测
# 预测数据
# vec2Classify表示待预测的数据向量
# p0Vec, p1Vec, pClass1分别对应着之前朴素贝叶斯模型的参数
# p0Vect表示在类别0中,各个词汇出现的概率向量
# p1Vect表示在类别1中,各个词汇出现的概率向量
# pAbusive表示训练集中,类别1的概率
def predictNB(vec2Classify,p0Vec, p1Vec, pClass1):
p1 = np.sum(vec2Classify * p1Vec) + np.log(pClass1) #∑p(xi)因为p1和p0都有,可以作为一个公系数略去。
p0 = np.sum(vec2Classify * p0Vec) + np.log(1 - pClass1)
if (p1>=p0): return 1
else: return 0
这里的vec2Classify即句子的词组成向量,句子中出现的单词置1,没出现的单词置0.
0乘任何数等于0,所以只有出现了的单词才会被计算,即实现了对公式:
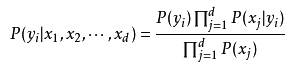
中x1,x2…,xj的筛选。
至于公式为什么长这样在第一部分已经做了推导。
运行结果

最后是数据集和代码:
链接:https://pan.baidu.com/s/10zKUxKP-_VTgRDMdF1k41g
提取码:axfz