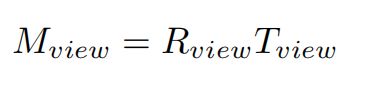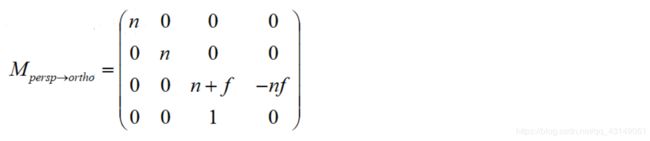【3】现代计算机图形学（正交投影，透视投影，MVP变换）
导读
本节主要总结MVP变换（Model-View-Projection），来说明三维空间中的物体是如何映射到二维屏幕上的。
知识点
-
View/Camera Transformation（视图/相机变换）
-
Projection Transformation（投影变换）
- Orthographics projection（正交投影）
- Persperctive projection（透视投影）
-
ViewPort Transformation（视口变换）
一、View/Camera Transformation（视图/相机变换）
1.1、什么是视图变换？
视图变换顾名思义就是把你所看到的图变换，举个简单的例子，打比方在日常生活中你去拍照，你首先会取景，然后把你想拍的东西都摆放好，这一步叫做model transformation（模型变换）。接下来你肯定会挑选一个特定的角度摆放你的摄像机，这一步就叫做view transformation（视图变换）。然后按下快门后把图片拍下来，这一步就叫做projection transformation（投影变换）。
1.2、怎样做视图变换？
了解了什么是视图变换，接下来就是怎么去做，做投影变换的前提是场景中得有一台摄像机，然后简单的给出几个物体。首先我们需要定义摄像机看向的方向为g（向量），然后取摄像机的向上方向为t（向量），再定义摄像机的位置position。
此时一个简单的场景就搭好了，现在我们需要做视图变换，一般在图形学中摄像机永远是看向-z方向，摄像机上边在y方向，所以需要将图示的摄像机变换到标准位置，但是这会出现一个问题，摄像机的位置一变，我们之前定义的g和t向量都会变换，这不是我们想看到的。
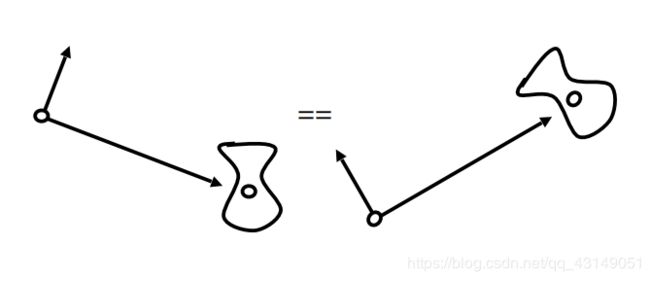
根据相对运动可知，如果所有物体和摄像机的位置一起改变一样的位置，那么摄像机看的画面就不会变。（比如你在中国的摄影棚拍照和在美国的摄影棚拍照，如果摄影棚的装饰完全一样，你所拍到的画面是没有区别的）
所以接下来就是写出视图变换矩阵了，但是此时我们又陷入了麻烦，将一个任意位置，任意方向的相机和物体，变换到标准位置（看向-z轴，顶部在y轴）是很困难去写这样的视图变换矩阵的。
常规做法：
- 先平移到原点
- 再将g旋转到-z
- 再将t旋转到y
- 再将g×t旋转到x
上述常规做法的变换矩阵是非常难写的，所以可用线性代数中的逆这一知识点简化写法。
简化做法：
- 平移到原点
- 由任意位置转换到标准位置改成由标准位置转化为任意位置
- 将求出的矩阵求逆矩阵
这样就简化了视图变换矩阵的求法，因为由任意位置转换到标准位置的矩阵是非常容易写的。
平移矩阵
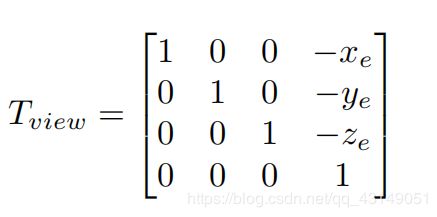
旋转矩阵
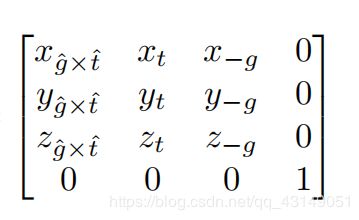
然后求该矩阵的逆
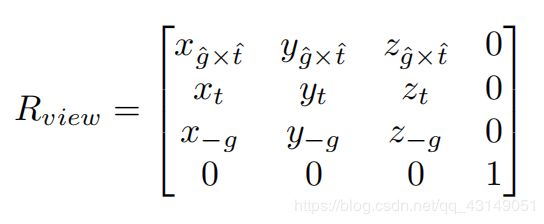
因为旋转矩阵是正交矩阵，所以求矩阵的逆就相当于求该矩阵的转置。
所以求得变换矩阵为
二、Projection Transformation（投影变换）
投影变换分为透视投影和正交投影，这两种投影的功能都是将3维空间的物体映射到二维空间。
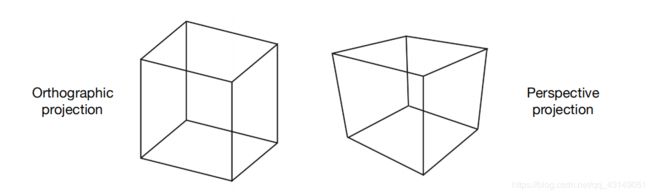
1、正交投影（Orthographic Projection）
1.1、什么是正交投影？
正交投影就是摄像机在原点，看向-z方向，顶部在y方向，在看向物体时将所有物体的z值归0，然后将物体平移并缩放到[-1,1]^2之间。
1.2、怎么做正交投影？
正交投影的做法就是把物体移到原点处的 [-1,1]^3 的标准立方体中。
步骤分为两步：
① 先将物体中心平移到原点。
②再进行缩放，缩放到[-1,1]^3 的标准立方体中。
这两个变换矩阵很好写出
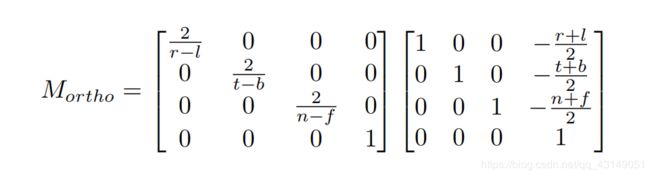
解释：平移矩阵中的这三个平移量得出的原因是因为要将中心平移到原点，所以要取每个轴的中心坐标，平移量为负的原因是将任意一个点平移到原点都是负的平移量。
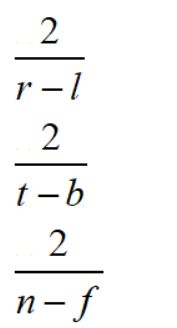
解释：缩放矩阵中的这三个缩放量得出的原因是用的[-1,1]的标准长度除以物体的每个轴所对应的长度，得到的缩放量。
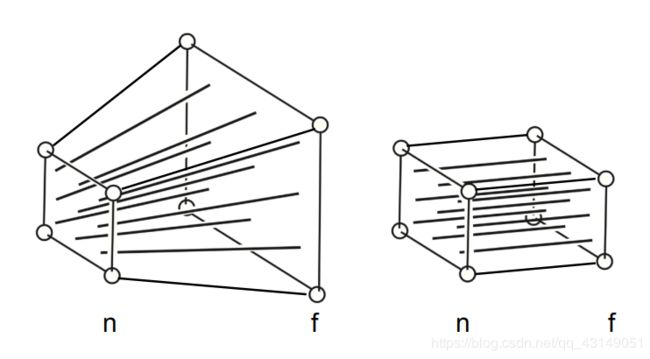
小提示：由于看向的是-z方向，所以近平面n要比远平面f大。
2、透视投影（Perspective Projection）
2.1、什么是透视投影？
简而言之，透视投影就是近大远小，平行线也会变得不平行，人们眼睛所看到的就是透视投影的结果。
2.2、怎么做透视投影？
常规法：硬性求解。此方法在各类图形学书中均有求解，在此暂不讨论。
由透视变换到正交解法：这种方法相对于复杂的常规解法要容易得多，下面我就说说具体的思路。
首先把透视投影“挤”成正交投影
然后再做正交投影
由于正交投影我们在上方已经解出，所以现在要做的就是如何写出“挤”这一步的变换矩阵。
首先观察下图
我们从截面观察各点的变化情况，由于远平面f要“挤”到和近平面一样大，所以可推导出图中远平面上的红点的y值会向下移动到y’这么高，所以由相似原理可写出
同理求得x的变化
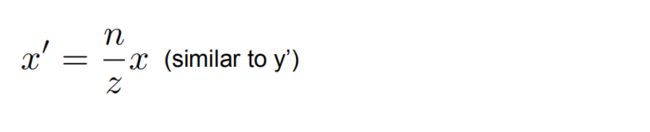
在齐次坐标中可以将原来远平面上的（x,y,z,1）的点写为：
为什么乘以z值之后得到的结果还相同？
因为在齐次坐标中，各个维度乘以相同的值得到点和原来一样。
此时可写出以下式子
由于已经知道了三行的值，所以可以逆推出透视变正交矩阵的三行的值
这是简单的线性代数矩阵和矩阵相乘的结果。
现在问题就简化为了如何求解矩阵第三行的值。
由于任何在近平面上的点是不会变的。
任何在远平面的点的z值也不会变。
由以上两条结论可推导出
n:近平面
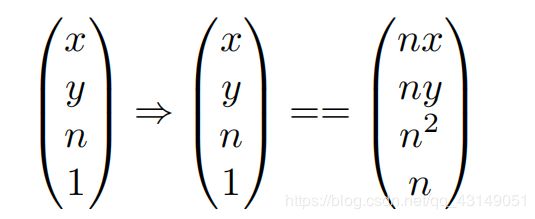
由于其他三行的值都已知，所以现在只用算第三行的值。又因为由近平面得出的第三行为n^2，所以可确定透视变正交矩阵第三行的前两维为0，所以可得：
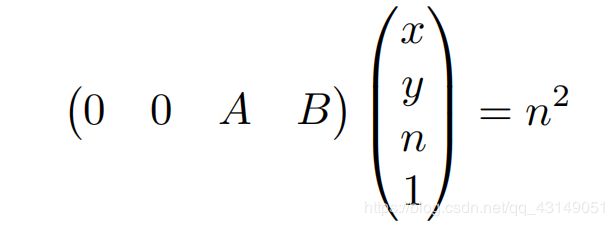
应用矩阵乘法，对应位置相乘，得：
再由第二条已知条件，所有在远平面的点的z值不变，可得（f为远平面）：
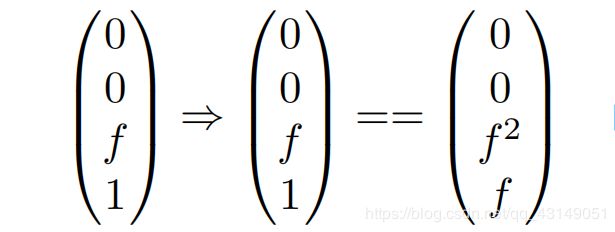
再和透视变正交矩阵的第三行相乘，得：
两个方程，两个未知量，可求得A与B的值
终于，所有求解工作完成，得到透视变正交矩阵
所以透视投影矩阵就等于正交投影矩阵乘以透视变正交矩阵
3、近平面的定义
定义近平面需要用到两个量，分别是fov(Field of view)和Aspect ratio。
fov是视角，这里又分为fovY和fovX，fovY是垂直视角，也就是从近平面的上边的中心和下边的中心分别连一条线到摄像机所成的角度，而fovX是水平视角。
Aspect ratio是宽高比，Aspect ratio = width/height。
三、ViewPort Transformation（视口变换）
1.1、什么是视口变换？
在我们做完投影变换后所有物体都映射在标准坐标系中，但是屏幕会有各种各样的分辨率，所以视口变换是为了将正常设备坐标映射到屏幕坐标。
1.2、怎么做视口变换？
假设屏幕的宽为width，高度为height，那么视口变换就是把[-1,1]^2的xy平面变到[0,width]x[0,height]，这里为什么没有考虑z轴的变换是因为z轴在之后的其他地方有用。
根据上述可得出视口变换矩阵为：
图片来自虚幻五游戏引擎实测场景
本文所有内容均是博主学习闫令琪老师的现代计算机图形学课程的总结，如有不足之处欢迎评论区指导补充。