数据结构—回溯法、子集树、排列树
文章目录
- 回溯法
- 问题的解空间
- 递归回溯
- 迭代回溯
- 子集树与排列树简单介绍
- 轮船装载问题
- 0-1背包问题
- 八皇后问题
- 整数求和(1)
- 整数求和(2)
- 全排列
回溯法
回溯法是一种以深度优先方式系统搜索问题解的算法,有“ 通用解题法”之称,可以系统地搜索一个问题的所有解或任一解,是一种既带有系统性又带有跳跃性的搜索算法。
回溯法搜索策略:
- 在问题的解空间树中,按深度优先策略
- 从根节点出发搜索解空间树
- 算法搜索至解空间树的任一结点时,先判断该结点是否包含问题的解
- 如果肯定不包含,则跳过以该结点为根的子树的搜索,逐层向其祖先结点回溯
- 否则,进入该子树,继续按深度优先策略搜索。
回溯法求问题的解时,要回溯到根,且根节点的所有子树都已经被搜索到才结束。
问题的解空间
用回溯法解问题时,应明确定义问题的解空间,问题的解空间至少应包含问题的一个(最优)解。
例如,对于有n种可选择物品的背包问题,其解空间由长度为 n 的0−1向量组成。该解空间包含对变量的所有可能的0-1赋值。
当n=3 时,其解空间如下:
{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1) }
定义了问题的解空间后,还应将解空间很好地组织起来,使得能用回溯法方便地搜索整个解空间。通常将解空间组织成树或图的形式。
例如,对于n=3时的背包问题,可用一棵完全二叉树表示其解空间,如下图所示。
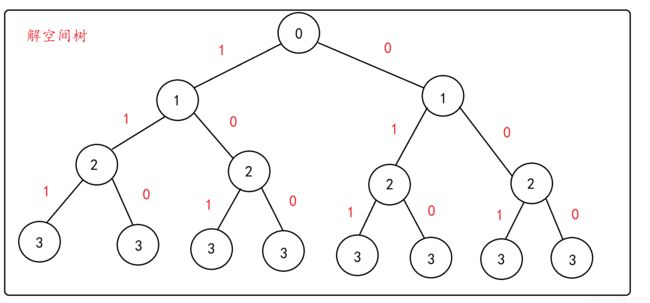
回溯法搜索解空间树时,通常采用两种策略来避免无效搜索,提高回溯法的搜索效率。
- 用约束函数在扩展结点处剪去不满足约束的子树
- 用限界函数剪去得不到最优解的子树。
- 这两类函数统称为剪枝函数。
用回溯法解题通常包含以下3个步骤:
- 针对所给问题,定义问题的解空间;
- 确定易于搜索的解空间结构;
- 以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
递归回溯
//形参t表示递归深度,即当前扩展结点在解空间树的深度
void backtrack(int t)
{
if (t > n)
{
output(x);//叶子节点,输出结果,x是可行解
}
else
{
for i = 1 to k//当前节点的所有子节点
{
x[t] = value(i); //每个子节点的值赋值给x
if (constraint(t) && bound(t))//满足约束条件和限界条件
backtrack(t + 1); //递归下一层
}
}
}
迭代回溯
void iterativeBacktrack ()
{
int t=1;
while (t>0) {
if(ExistSubNode(t)) //当前节点的存在子节点
{
for i = 1 to k //遍历当前节点的所有子节点
{
x[t]=value(i);//每个子节点的值赋值给x
if (constraint(t)&&bound(t))//满足约束条件和限界条件
{
//solution表示在节点t处得到了一个解
if (solution(t)) output(x);//得到问题的一个可行解,输出
else t++;//没有得到解,继续向下搜索
}
}
}
else //不存在子节点,返回上一层
{
t--;
}
}
}
用回溯法解题的一个显著特征是在搜索过程中动态产生问题的解空间。在任何时刻,算法只保存从根结点到当前扩展结点的路径。
如果解空间树中从根结点到叶结点的最长路径的长度为 h ( n ) h(n) h(n),则回溯法所需的计算空间通常为 O ( h ( n ) ) O(h(n)) O(h(n))。而显式地存储整个解空间则需要 O ( 2 h ( n ) ) O(2^{h(n)}) O(2h(n)) 内存空间。
子集树与排列树简单介绍
当所给的问题是从 n 个元素的集合 S 中找出满足某种性质的子集时,相应的解空间树称为子集树。
例如:n个物品的0-1背包问题所相应的解空间树就是一棵子集树。
- 这类子集树通常有 2 n 2^n 2n 个叶结点,其结点总个数为 2 n + 1 − 1 2^{n+1}-1 2n+1−1。
- 遍历子集树的任何算法均需 O ( 2 n ) O(2^n) O(2n)的计算时间。
用回溯法搜索子集树的一般算法可描述如下:
void Backtrace(int t)
{
if (t > n)
{
Output(x);
}
else
{
for (int i = 0; i <= 1; i++)
{
x[t] = i;
}
if (Constrain(t) && Bound(t))
{
Backtrace(t + 1);
}
}
}
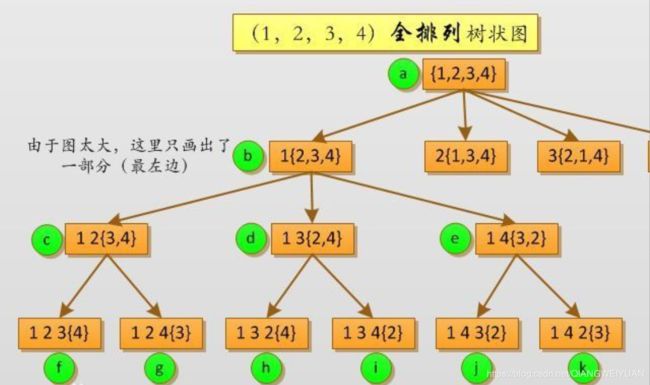
当所给的问题是确定 n 个元素满足某种性质的排列时,相应的解空间树称为排列树。
例如:旅行商问题的解空间树就是一棵排列树。
- 排列树通常有 n ! n! n!个叶结点。
- 因此遍历排列树需要 O ( n ! ) O(n!) O(n!)的计算时间
用回溯法搜索排列树的一般算法可描述如下:
void Backtrace(int t)
{
if (t > n)
{
Output(x);
}
else
{
for (int i = t; i <= n; ++i)
{
Swap(x[t], x[i]);
if (Constrain(t) && Bound(t))
{
Backtrace(t + 1);
}
Swap(x[t], x[i]);
}
}
}
轮船装载问题
问题描述
有一批共n个集装箱要装上2艘载重量分别为 c 1 c1 c1和 c 2 c2 c2的轮船,其中集装箱i的重量为 w i wi wi,且集装箱重量总和 ( w 1 + w 2 + … + w n ) (w1+w2+…+wn) (w1+w2+…+wn)< c 1 + c 2 c1+c2 c1+c2。
要求确定一种合理的装载方案将这n个集装箱装上这2艘船。
算法描述
用回溯法解装载问题时,用子集树表示其解空间显然是最合适的。可行性约束函数可剪去不满足约束条件的子树。
/*
* 首先将第一艘轮船尽可能装满
* 将剩余的集装箱装上第二艘轮船
* 将第一艘轮船尽可能装满等价于选取集装箱的一个子集,使该子集中集装箱重量之和最接近第一艘轮船的重量c1
* 因此,装载问题等价于特殊的0-1背包问题
*/
#include<iostream>
using namespace std;
const int N = 7;
int w[] = { 7,8,5,9,4,6,3 };//集装箱的重量
int c1 = 22;//第一艘船的载重量
int c2 = 20;//第二艘船的载重量
int x[N];//辅助数组
int cw;//当前已选取的集装箱的重量和
int bestw;//当前选取的最优重量
int bestx[N];//最优结果集
int r;
void func(int i)
{
if (i == N)//到达叶子结点
{
/*
* 当前选取的重量和大于最优解
* 最优解进行更新
* 最优结果集进行更新
*/
if (cw > bestw)
{
bestw = cw;
for (int j = 0; j < N; ++j)
{
bestx[j] = x[j];
}
}
}
else//还未到达叶子节点
{
r -= w[i];
if (cw + w[i] <= c1) // i节点左子树的剪枝操作
{
cw += w[i];
x[i] = 1;
func(i + 1);
cw -= w[i];
}
/*
* i节点右子树的剪枝操作
* 当当前已选取的重量和与右子树能够选取得重量和大于当前已经得到得到的最优解时
* 才需要进入右子树
* 否则进行剪枝操作
*/
if (cw + r > bestw)
{
x[i] = 0;
func(i + 1);
}
r += w[i];
}
}
int main()
{
for (int w1 : w)
{
r += w1;
}
func(0);
cout << "轮船c1:" << c1 << "装入的物品是:";
for (int i = 0; i < N; ++i)
{
if (bestx[i] == 1)
{
cout << w[i] << " ";
}
}
cout << endl;
cout << "轮船c2:" << c2 << "装入的物品是:";
for (int i = 0; i < N; ++i)
{
if (bestx[i] == 0)
{
cout << w[i] << " ";
}
}
cout << endl;
return 0;
}
0-1背包问题
问题描述
有一个贼在偷窃一家商店时,发现有n件物品,第i件物品价值vi元,重wi磅,此处vi与wi都是整数。他希望带走的东西越值钱越好,但他的背包中至多只能装下W磅的东西,W为一整数。应该带走哪几样东西?这个问题之所以称为0-1背包,是因为每件物品或被带走,或被留下;小偷不能只带走某个物品的一部分或带走同一物品两次。
算法描述
0-1背包问题是子集选取问题。在搜索解空间树时,只要其左儿子结点是一个可行结点,搜索就进入其左子树。当右子树中有可能包含最优解时才进入右子树搜索;否则就将右子树剪去。
代码实现:
#include<iostream>
using namespace std;
const int N = 5;
int w[] = { 8,4,9,6,7 };
int v[] = { 7,9,6,12,3 };
int c = 18;
int x[N]; // 辅助数组
int bestx[N]; // 记录最优子集的数组
int cw; // 记录选择的物品的重量
int cv; // 记录选择物品的价值
int r; // 记录节点右子树中剩余能够选择的物品的总价值
int bestv = 0; // 记录选择的物品的最优价值
// 输出最终选择的物品和最大价值
void func(int i)
{
if (i == N)
{
if (cv > bestv)
{
bestv = cv;
for (int j = 0; j < N; ++j)
{
bestx[j] = x[j];
}
}
}
else
{
r -= v[i];
if (cw + w[i] <= c)//i结点左子树的剪枝操作
{
cw += w[i];
cv += v[i];
x[i] = 1;
func(i + 1);
cw -= w[i];
cv -= v[i];
}
/*
* 如果当前已选择物品的价值+右子树可选物品的价值<目前的最优解
* 就不必再去右子树,称之对右子树的剪枝
*/
if (cv + r > bestv)
{
x[i] = 0;
func(i + 1);
}
r += v[i];
}
}
int main()
{
for (int v1 : v)
{
r += v1;
}
func(0);
cout << "best value:" << bestv << endl;
for (int i = 0; i < N; ++i)
{
if (bestx[i])
{
cout << v[i] << " ";
}
}
cout << endl;
return 0;
}
八皇后问题
问题描述
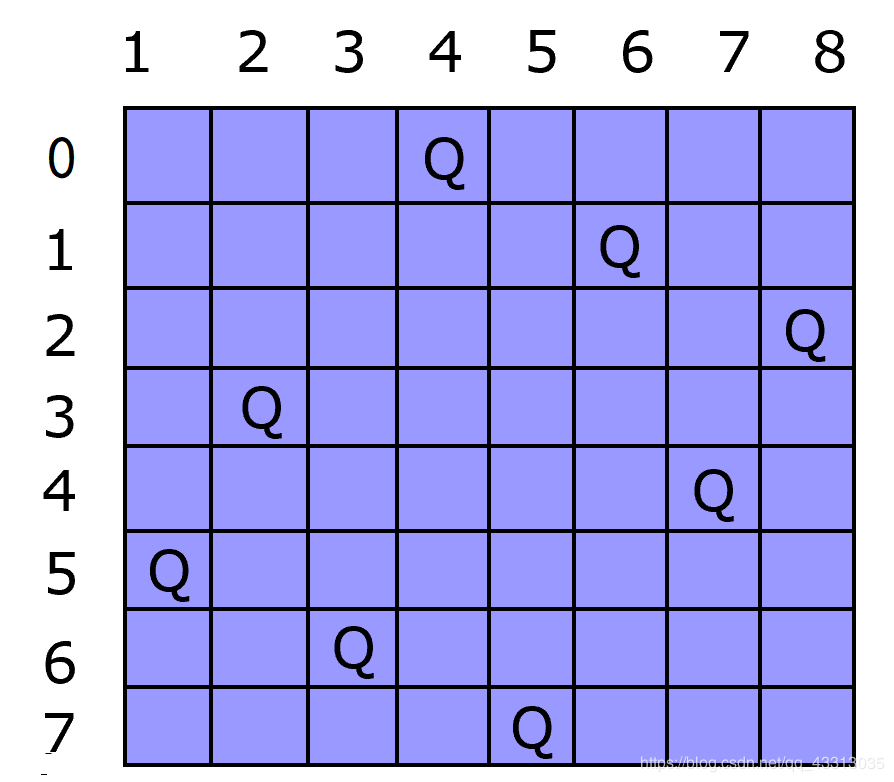
在n×n的棋盘上放置彼此不受攻击的n个皇后。
按照国际象棋的规则,皇后可以攻击与之处于同一行或同一列或统一斜线上的棋子。
n皇后问题等价于在n×n的棋盘上放置n个皇后,任意2个皇后不能放在同一行或同一列或同一斜线上
算法描述
用n元组ar[1:n]表示n后问题的解。其中ar[i]表示第i个皇后放在棋盘的第i行第ar[i]列。由于不允许将2个皇后放在同一列上,所以解向量中的ar[i]互不相同。
/*
* 由于我们的数组下标代表行数,元素代表列数,且每个元素值不相等
* 因此,八个皇后一定不会处在同一行或同一列
* 只需要排除处于同一条斜线上的情况
*/
#include<iostream>
using namespace std;
const int N = 8;
int ar[] = { 1,2,3,4,5,6,7,8 }; // 数组的index,代表行数
int cn = 0;//符合条件的排列组合的个数
void swap(int i, int j)
{
int tmp = ar[i];
ar[i] = ar[j];
ar[j] = tmp;
}
bool isline(int i) //判断是否处在同一条斜线上
{
for (int j = 0; j < i; ++j)
{
if (i - j == abs(ar[i] - ar[j]))
{
return false;
}
}
return true;
}
void func(int i)
{
if (i == N)
{
cn++;
for (int k = 0; k < N; ++k)
{
// k代表行数,ar[k]代表列数
cout << "{" << k << "," << ar[k] << "}" << ",";
}
cout << endl;
}
else
{
for (int j = i; j < N; ++j)
{
swap(i, j);
if (isline(i))
{
func(i+1);
}
swap(i, j);
}
}
}
int main()
{
func(0);
cout<<cn<<endl;
return 0;
}
{0,1} {1,5} {2,8} {3,6} {4,3} {5,7} {6,2} {7,4}
{0,1} {1,6} {2,8} {3,3} {4,7} {5,4} {6,2} {7,5}
{0,1} {1,7} {2,4} {3,6} {4,8} {5,2} {6,5} {7,3}
{0,1} {1,7} {2,5} {3,8} {4,2} {5,4} {6,6} {7,3}
{0,2} {1,4} {2,6} {3,8} {4,3} {5,1} {6,7} {7,5}
{0,2} {1,5} {2,7} {3,4} {4,1} {5,8} {6,6} {7,3}
{0,2} {1,5} {2,7} {3,1} {4,3} {5,8} {6,6} {7,4}
{0,2} {1,6} {2,1} {3,7} {4,4} {5,8} {6,3} {7,5}
{0,2} {1,6} {2,8} {3,3} {4,1} {5,4} {6,7} {7,5}
{0,2} {1,7} {2,3} {3,6} {4,8} {5,5} {6,1} {7,4}
{0,2} {1,7} {2,5} {3,8} {4,1} {5,4} {6,6} {7,3}
{0,2} {1,8} {2,6} {3,1} {4,3} {5,5} {6,7} {7,4}
{0,3} {1,1} {2,7} {3,5} {4,8} {5,2} {6,4} {7,6}
{0,3} {1,5} {2,2} {3,8} {4,1} {5,7} {6,4} {7,6}
{0,3} {1,5} {2,2} {3,8} {4,6} {5,4} {6,7} {7,1}
{0,3} {1,5} {2,7} {3,1} {4,4} {5,2} {6,8} {7,6}
{0,3} {1,5} {2,8} {3,4} {4,1} {5,7} {6,2} {7,6}
{0,3} {1,6} {2,4} {3,1} {4,8} {5,5} {6,7} {7,2}
{0,3} {1,6} {2,4} {3,2} {4,8} {5,5} {6,7} {7,1}
{0,3} {1,6} {2,2} {3,5} {4,8} {5,1} {6,7} {7,4}
{0,3} {1,6} {2,2} {3,7} {4,5} {5,1} {6,8} {7,4}
{0,3} {1,6} {2,2} {3,7} {4,1} {5,4} {6,8} {7,5}
{0,3} {1,6} {2,8} {3,2} {4,4} {5,1} {6,7} {7,5}
{0,3} {1,6} {2,8} {3,1} {4,5} {5,7} {6,2} {7,4}
{0,3} {1,6} {2,8} {3,1} {4,4} {5,7} {6,5} {7,2}
{0,3} {1,7} {2,2} {3,8} {4,5} {5,1} {6,4} {7,6}
{0,3} {1,7} {2,2} {3,8} {4,6} {5,4} {6,1} {7,5}
{0,3} {1,8} {2,4} {3,7} {4,1} {5,6} {6,2} {7,5}
{0,4} {1,2} {2,5} {3,8} {4,6} {5,1} {6,3} {7,7}
{0,4} {1,2} {2,7} {3,5} {4,1} {5,8} {6,6} {7,3}
{0,4} {1,2} {2,7} {3,3} {4,6} {5,8} {6,1} {7,5}
{0,4} {1,2} {2,7} {3,3} {4,6} {5,8} {6,5} {7,1}
{0,4} {1,2} {2,8} {3,5} {4,7} {5,1} {6,3} {7,6}
{0,4} {1,2} {2,8} {3,6} {4,1} {5,3} {6,5} {7,7}
{0,4} {1,1} {2,5} {3,8} {4,6} {5,3} {6,7} {7,2}
{0,4} {1,1} {2,5} {3,8} {4,2} {5,7} {6,3} {7,6}
{0,4} {1,6} {2,1} {3,5} {4,2} {5,8} {6,3} {7,7}
{0,4} {1,6} {2,8} {3,2} {4,7} {5,1} {6,3} {7,5}
{0,4} {1,6} {2,8} {3,3} {4,1} {5,7} {6,5} {7,2}
{0,4} {1,7} {2,3} {3,8} {4,2} {5,5} {6,1} {7,6}
{0,4} {1,7} {2,1} {3,8} {4,5} {5,2} {6,6} {7,3}
{0,4} {1,7} {2,5} {3,3} {4,1} {5,6} {6,8} {7,2}
{0,4} {1,7} {2,5} {3,2} {4,6} {5,1} {6,3} {7,8}
{0,4} {1,8} {2,1} {3,3} {4,6} {5,2} {6,7} {7,5}
{0,4} {1,8} {2,1} {3,5} {4,7} {5,2} {6,6} {7,3}
{0,4} {1,8} {2,5} {3,3} {4,1} {5,7} {6,2} {7,6}
{0,5} {1,2} {2,4} {3,6} {4,8} {5,3} {6,1} {7,7}
{0,5} {1,2} {2,4} {3,7} {4,3} {5,8} {6,6} {7,1}
{0,5} {1,2} {2,6} {3,1} {4,7} {5,4} {6,8} {7,3}
{0,5} {1,2} {2,8} {3,1} {4,4} {5,7} {6,3} {7,6}
{0,5} {1,3} {2,1} {3,6} {4,8} {5,2} {6,4} {7,7}
{0,5} {1,3} {2,1} {3,7} {4,2} {5,8} {6,6} {7,4}
{0,5} {1,3} {2,8} {3,4} {4,7} {5,1} {6,6} {7,2}
{0,5} {1,1} {2,4} {3,6} {4,8} {5,2} {6,7} {7,3}
{0,5} {1,1} {2,8} {3,4} {4,2} {5,7} {6,3} {7,6}
{0,5} {1,1} {2,8} {3,6} {4,3} {5,7} {6,2} {7,4}
{0,5} {1,7} {2,4} {3,1} {4,3} {5,8} {6,6} {7,2}
{0,5} {1,7} {2,1} {3,4} {4,2} {5,8} {6,6} {7,3}
{0,5} {1,7} {2,1} {3,3} {4,8} {5,6} {6,4} {7,2}
{0,5} {1,7} {2,2} {3,4} {4,8} {5,1} {6,3} {7,6}
{0,5} {1,7} {2,2} {3,6} {4,3} {5,1} {6,4} {7,8}
{0,5} {1,7} {2,2} {3,6} {4,3} {5,1} {6,8} {7,4}
{0,5} {1,8} {2,4} {3,1} {4,3} {5,6} {6,2} {7,7}
{0,5} {1,8} {2,4} {3,1} {4,7} {5,2} {6,6} {7,3}
{0,6} {1,2} {2,7} {3,1} {4,4} {5,8} {6,5} {7,3}
{0,6} {1,2} {2,7} {3,1} {4,3} {5,5} {6,8} {7,4}
{0,6} {1,3} {2,5} {3,7} {4,1} {5,4} {6,2} {7,8}
{0,6} {1,3} {2,5} {3,8} {4,1} {5,4} {6,2} {7,7}
{0,6} {1,3} {2,1} {3,7} {4,5} {5,8} {6,2} {7,4}
{0,6} {1,3} {2,1} {3,8} {4,5} {5,2} {6,4} {7,7}
{0,6} {1,3} {2,1} {3,8} {4,4} {5,2} {6,7} {7,5}
{0,6} {1,3} {2,7} {3,4} {4,1} {5,8} {6,2} {7,5}
{0,6} {1,3} {2,7} {3,2} {4,4} {5,8} {6,1} {7,5}
{0,6} {1,3} {2,7} {3,2} {4,8} {5,5} {6,1} {7,4}
{0,6} {1,4} {2,2} {3,8} {4,5} {5,7} {6,1} {7,3}
{0,6} {1,4} {2,1} {3,5} {4,8} {5,2} {6,7} {7,3}
{0,6} {1,4} {2,7} {3,1} {4,3} {5,5} {6,2} {7,8}
{0,6} {1,4} {2,7} {3,1} {4,8} {5,2} {6,5} {7,3}
{0,6} {1,1} {2,5} {3,2} {4,8} {5,3} {6,7} {7,4}
{0,6} {1,8} {2,2} {3,4} {4,1} {5,7} {6,5} {7,3}
{0,7} {1,2} {2,4} {3,1} {4,8} {5,5} {6,3} {7,6}
{0,7} {1,2} {2,6} {3,3} {4,1} {5,4} {6,8} {7,5}
{0,7} {1,3} {2,1} {3,6} {4,8} {5,5} {6,2} {7,4}
{0,7} {1,3} {2,8} {3,2} {4,5} {5,1} {6,6} {7,4}
{0,7} {1,4} {2,2} {3,5} {4,8} {5,1} {6,3} {7,6}
{0,7} {1,4} {2,2} {3,8} {4,6} {5,1} {6,3} {7,5}
{0,7} {1,5} {2,3} {3,1} {4,6} {5,8} {6,2} {7,4}
{0,7} {1,1} {2,3} {3,8} {4,6} {5,4} {6,2} {7,5}
{0,8} {1,2} {2,4} {3,1} {4,7} {5,5} {6,3} {7,6}
{0,8} {1,2} {2,5} {3,3} {4,1} {5,7} {6,4} {7,6}
{0,8} {1,3} {2,1} {3,6} {4,2} {5,5} {6,7} {7,4}
{0,8} {1,4} {2,1} {3,3} {4,6} {5,2} {6,7} {7,5}
92
{0,4} {1,6} {2,8} {3,2} {4,7} {5,1} {6,3} {7,5}
整数求和(1)
问题描述
有一组整数,请选择一部分整数,使选择的整数的和,和剩下的整数的和的差最小
#include<iostream>
using namespace std;
#define N 10
int arr[N] = { 12, 3, 45, 6, 78, 9, 43, 21, 62, 31 };
// 辅助数组
int brr[N] = { 0 };
// 存储标志位,标志最终的结果集
int res[N] = { 0 };
// 序列中剩余数字的和
int arrSum = 0;
// 当前选择序列的和
//int sum = 0;
// 存储当前的最小差值
unsigned int min = 0xFFFFFFFF;
void func(int i)
{
if (i == N)
{
int sum = 0;
for (int j = 0; j < N; ++j)
{
if (brr[j] == 1)
{
// 求当前选择的序列的和
sum += arr[j];
}
}
//int diff = abs(sum - (arrSum - sum));
int diff = abs(sum - arrSum);
/* 当前的差值比记录的最小差值还要小,进行更新 */
if (diff < min)
{
min = diff;
for (int k = 0; k < N; k++)
{
res[k] = brr[k];
}
}
}
else
{
/* 左子树中剩余的元素和,arrSum减去选择的元素 */
arrSum -= arr[i];
brr[i] = 1;
func(i + 1);
/* 右子树中的元素不被选择,arrSum加上该元素 */
arrSum += arr[i];
brr[i] = 0;
func(i + 1);
}
}
int main()
{
for (int i = 0; i < N; i++)
{
arrSum += arr[i];
}
func(0);
for (int i = 0; i < N; i++)
{
if (res[i] == 1)
{
cout << arr[i] << " ";
}
}
cout << endl;
cout << "min:" << min << endl;
return 0;
}
整数求和(2)
问题描述
有一组2n个整数,请选择n个整数,使选择的整数的和,和剩下的整数的和的差最小
int ar[] = { 12,3,45,6,78,9,43,22,62,31 };
const int N = 10;
int x[N]; // 子集树遍历的辅助数组
int bestx[N]; // 记录最优解的子集
int sum; // 记录所选子集数字的和
int r; // 记录未选择的数字的和
int cnt; // 记录选择的子集的个数
unsigned int min = 0xFFFFFFFF;
int mycount = 0;
void func(int i)
{
if (i == N)
{
mycount++;
if (cnt != N / 2)
return;
int ret = abs(sum - r);
if (min > ret)
{
min = ret;
for (int j = 0; j < N; ++j)
{
bestx[j] = x[j];
}
}
}
else
{
if (cnt < N / 2)
{
r -= ar[i];
sum += ar[i];
cnt++; // if(cnt < N/2)
x[i] = 1;
func(i + 1);
cnt--;
sum -= ar[i];
r += ar[i];
x[i] = 0;
func(i + 1);
}
}
}
int main()
{
for (int val : ar)
r += val;
func(0);
cout << "min:" << min << endl;
for (int i = 0; i < N; ++i)
{
if (bestx[i] == 1)
{
cout << ar[i] << " ";
}
}
cout << endl;
cout << "mycount:" << mycount << endl;
return 0;
}
全排列
#include<iostream>
using namespace std;
void swap(int *arr, int i, int j)
{
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
void fun(int *arr,int i,int length)
{
if (i == length)
{
for (int j = 0; j < length; ++j)
{
cout << arr[j] << " ";
}
cout << endl;
}
else
{
//由于递归每深入一层就能多固定一个数,因此j只需要从i开始
for (int j = i; j < length;++j)
{
swap(arr, i,j);
fun(arr, i + 1, length);
swap(arr, i,j);
}
}
}
int main()
{
int arr[] = { 1,2,3,4 };
int len = sizeof(arr) / sizeof(arr[0]);
fun(arr, 0, len);
return 0;
}
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 3 2
1 4 2 3
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 3 1
2 4 1 3
3 2 1 4
3 2 4 1
3 1 2 4
3 1 4 2
3 4 1 2
3 4 2 1
4 2 3 1
4 2 1 3
4 3 2 1
4 3 1 2
4 1 3 2
4 1 2 3