遗传算法应用实例
文章目录
- 生物学中的遗传
- 遗传算法所能解决的问题
- 生物遗传图解
- 遗传算法图解
- 代码实现解决数组分割问题
- 适应度计算
- 选择进入下一代的个体
- 交叉因子的计算
- 变异
- 主函数调用已经其他辅助函数
生物学中的遗传
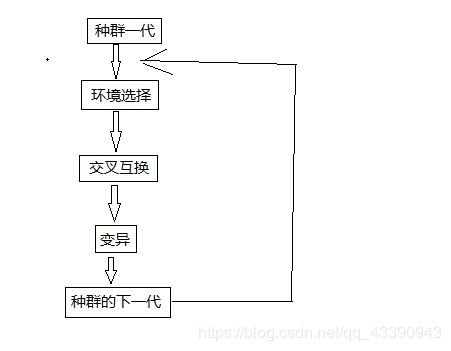
假设将一个种群放到一个新的环境中,在环境不变的情况下,种群中适应环境的个体的基因遗传到下一代的概率就会大,不适应环境的个体的基因遗传到下一代的概率就会小,在进行N次迭代后,种群中不适应环境的基因就会逐渐消失,保留下来的都是对环境适应度高的基因。
但仅仅依靠外部的环境选择是远远不能达到我们现在的生物的多样性的,因为生物的遗传过程中还存在着基因的交叉互换和基因的变异。
遗传算法所能解决的问题
遗传算法无法确定性的给出问题的具体解,因为在遗传过程中存在着不确定因素,但能够保证在迭代次数足够多的时候,能给出问题的近似解。如果求的是最优解问题,遗传算法不一定能够得到最优解,但可以得到相对较优的解。所以,该算法适用于对解的精确度要求不高的一些问题。在概率计算中应用较广。
生物遗传图解
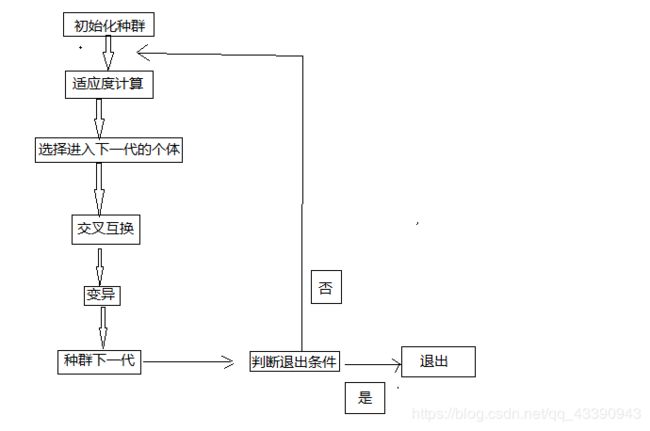
遗传算法图解
代码实现解决数组分割问题
一个有100个整数的数组中取10个元素,使得这10个元素的值接近于数组总值的1/10
适应度计算
//arr[][]表示选择出来的种群,这里是10和数组长度为10的二维数组
//mid 表示数组总和的1/10
//yarr 表示原来的数组
int Suff(int arr[ROW][COL],int mid,int len,int n,int *yarr,double *suf)
{
double suff = 0;
int num = 0; //子数组的和
for(int i = 0; i < n; i++)
{
num = Sum(arr[i],len,yarr); //求arr[i]数组中10个元素的和
num = abs(num-mid); //子数组和减去原数组的和的1/10
if (num == 0)
{
return i; //如果找到满足条件子数组,直接返回,不再迭代
}
suff += (double)1/num; //累加总的适应度
num = 0; //循环求解
}
*suf = suff; //将总的适应度带回
return -1; //返回总的适应度
}
Sum 求和函数
int Sum(int *arr,int len,int *yarr)
{
int sum = 0;
for(int i = 0; i < len; i++)
{
sum += yarr[arr[i]]; //arr[]中存放的是yarr总数组的下标
}
return sum;
}
选择进入下一代的个体
//选择算子设计 选出下一代个体
//index[] 记录进入下一代的个体
void Subarrs(int arr[ROW][COL],int mid,double suff
,int n,int len,int index[LEN],int *yarr)
{
double corona[LEN] = {0};
int num = 0;
//通过轮盘赌的方法构造一个数组,将数组分段,每个段代表一个个体进入下一代的概率
//如果此处不明白,可自行查看轮盘赌构造方法
for(int i = 0; i < LEN; i++) //构造轮盘
{
num = Sum(arr[i],len,yarr);
num = abs(num-mid);
if(i > 0)
{
corona[i] = corona[i-1] + ((double)1/num)/suff;
}
else
{
corona[i] = ((double)1/num)/suff;
}
}
for(int i = 0; i < LEN; i++) //LEN代表遗传到下一代的个数
{
float f = rand()%10000; //随机选择遗传到下一代
f /= 10000;
for(int j = 0; j < LEN; j++)
{
if(corona[j] >= f)
{
index[j]++; //记录进入下一代的个体的下标
break;
}
}
}
}
交叉因子的计算
两个个体进行交叉互换的时候,保证两个相互交换的基因不能相同,否则的还交换就不会引起两个数组的改变,同一个数组中不能包含两个相同的元素,因为题目要求选择10个不同的数组元素。否则可能一个元素,在一个数组中被选择了两次
int Select(int arr[ROW][COL],int row1,int row2,int *sub)
{
//随机选择一个 个体
int sub1 = rand()%COL;
//如果前面两个条件一直不满足,就用count计数结束下面的循环
int count = 0;
for(int j = 0; j < COL; j++)
{
if(arr[row1][j] == arr[row2][sub1])
{
count++;
//随机选择数组中的一个元素
sub1 = rand()%COL;
j = -1;
}
if(count == 20)
{
return -1;
}
}
//记录以下被选中的个体,返回进行互换
*sub = sub1;
return 0;
}
//交叉算子 arr[][]存放原数组的下标
void Crossover(int arr[ROW][COL])
{
//srand(time(0));
for(int i = 0; i < LEN; i += 2)
{
int sub1 = 0;
int tag1 = Select(arr,i+1,i,&sub1);
int sub2 = 0;
int tag2 = Select(arr,i,i+1,&sub2);
if(tag1 == 0 && tag2 == 0) //随机值产生正常进行互换
{
int tmp = arr[i][sub1];
arr[i][sub1] = arr[i+1][sub2];
arr[i+1][sub2] = tmp;
}
}
}
变异
变异同样要满足交叉互换的条件,不能变为本数组中已有的元素
int MutaIndex(int arr[ROW][COL],int row)
{
int sub = rand()%(10*COL);
//查找变异的元素是否在数组中已经包含
for(int j = 0; j < COL; j++)
{
//如果已经包含,重新选择
if(sub == arr[row][j])
{
sub = rand()%(10*COL);
}
}
return sub;
}
//变异算子
void Mutation(int arr[ROW][COL])
{
for(int i = 0; i < LEN; i++)
{
float f = rand()%10000;
f /= 10000;
//MUTATION 表示变异的概率,不是每个个体都会变异。这样能够保证适应度较高的个体
//不会过多的产生变异
if(f < MUTATION)
{
int sub = MutaIndex(arr,i);
int seat = rand()%COL;
arr[i][seat] = sub;
}
}
}
主函数调用已经其他辅助函数
```//数组赋值
void ArrEva(int *des,int *src,int len)
{
for(int i = 0; i < len; i++)
{
des[i] = src[i];
}
}
void ArrTwoEva(int arr[ROW][COL],int *index)
{
for(int i = 0; i < LEN; i++)
{
if(index[i] == 0)
{
for(int j = 0; j < LEN; j++)
{
if(index[j] > 1)
{
ArrEva(arr[i],arr[j],COL);
index[j]--;
index[i]++;
break;
}
}
}
}
}
void Show(int arr[ROW][COL],int row,int col,int *yarr)
{
int sum = 0;
for(int i = 0; i < ROW; i++)
{
for(int j = 0; j < COL; j++)
{
printf("%5d",yarr[arr[i][j]]);
sum += yarr[arr[i][j]];
}
printf(" %d\n",sum);
sum = 0;
}
}
void Print(int *arr,int len)
{
int sum = 0;
for(int i = 0; i < len; i++)
{
sum += arr[i];
printf("%d ",arr[i]);
}
printf(" %d \n",sum);
}
int main()
{
srand(time(0));
int yarr[100] = {0};
for(int i = 0; i < 100; i++)
{
yarr[i] = i;
}
//计算数组值的1/10
int mid = 0;
for(int i = 0; i < 100; i++)
{
mid += yarr[i];
}
mid /= 10;
//初始化种群
int arr[ROW][COL] = {0};
for(int i = 0; i < ROW; i++)
{
for(int j = 0; j < COL; j++)
{
arr[i][j] = (i+1)*(j+1)-1;
}
}
for(int i = 0; i < 30; i++)
{
double suff = 0;
int tag = Suff(arr,mid,COL,ROW,yarr,&suff);
if(tag != -1)
{
Print(arr[tag],COL);
return 0;
}
int index[LEN] = {0}; //遗传下一代的个体索引
//遗传到下一代的值
Subarrs(arr,mid,suff,ROW,COL,index,yarr);
ArrTwoEva(arr,index);
Crossover(arr);
Mutation(arr);
}
Show(arr,ROW,COL,yarr);
return 0;
}