#机器学习--第4章:建模调参之决策树与随机森林初体验
#机器学习--第4章:建模调参之决策树与随机森林初体验
- 一、原理概述
- 二、算法实现
序言:本系列博客面向初学者,只讲浅显易懂易操作的知识。
一、原理概述
不知初学编程时的你是否和我一般,曾异想天开地想,游戏是不是由很多很多 if 写出来的,或者我能不能用一万行 if 来写一个程序或算法。
而决策树,在某种程度来说,就是由很多很多 if 构成的算法。
决策树其实在我们生活中随处可见,就比如,我们在决定是否买一双鞋子的时候,会综合考虑这双鞋子的价格、颜色、款式、码数、布料等因素,例如,价格如果高于某个临界值,我们就不会购买,码数如果大于某个值,小于某个值,我们也不会购买…只有当这些都符合自己心意的时候,我们才会考虑购买,所以这个过程大致如下:
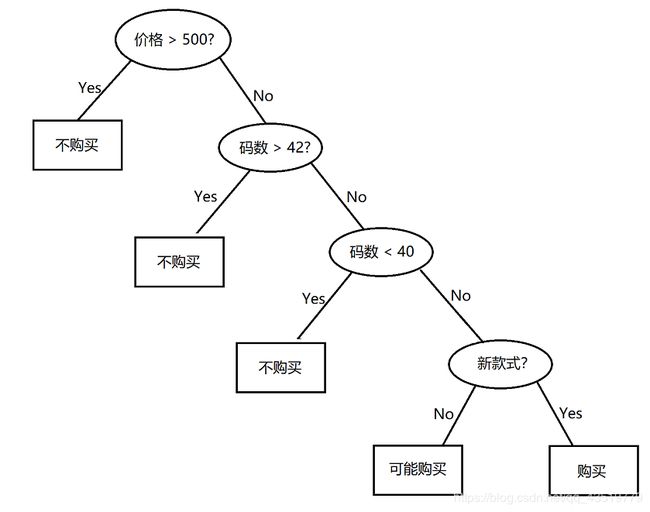
但是这么多 if ,不可能我们自己一个一个手写过去,而且有的人觉得款式比价格更重要,应该把款式放根结点,无法有一个统一的标准,所以就有了决策树算法,它能够自动的生成一棵最好的决策树。要最好,就得有好坏的衡量指标:“熵”和“基尼指数”
我们在高中化学都学过“熵”,它描述了一个系统的混乱程度,熵越大,系统混乱程度越高,纯度越低。
计算公式为: E n t r o p y = − ∑ p i ⋅ l o g ( p i ) {Entropy = -\sum p_{i}\cdot log(p_{i})} Entropy=−∑pi⋅log(pi),其中 p i {p_{i}} pi 表示类 i {i} i 的数量占比
例如:
价格不大于 500 的熵为
E n t r o p y = − ( p n o b u y ⋅ l o g ( p n o b u t ) + p b u y ⋅ l o g ( p b u t ) + p m a y b e b u y ⋅ l o g ( p m e y b e b u t ) ) = − ( 0.5 ⋅ l o g 0.5 + 2 ⋅ 0.25 ⋅ l o g 0.25 ) ≈ 0.45 {Entropy = -(p_{nobuy}\cdot log(p_{nobut})+p_{buy}\cdot log(p_{but})+p_{maybebuy}\cdot log(p_{meybebut}))=-(0.5\cdot log0.5+ 2\cdot 0.25\cdot log0.25)\approx 0.45} Entropy=−(pnobuy⋅log(pnobut)+pbuy⋅log(pbut)+pmaybebuy⋅log(pmeybebut))=−(0.5⋅log0.5+2⋅0.25⋅log0.25)≈0.45
价格小于 500 的熵为
E n t r o p y = − ( p n o b u y ⋅ l o g ( p n o b u t ) ) = − ( 1 ⋅ l o g 1 ) = 0 {Entropy = -(p_{nobuy}\cdot log(p_{nobut}))=-(1\cdot log1)=0} Entropy=−(pnobuy⋅log(pnobut))=−(1⋅log1)=0
基尼指数和熵起始也差不多基尼指数越大,系统纯度越低。
计算公式为: G i n i = 1 − ∑ p i 2 {Gini = 1 - \sum p_{i}^{2}} Gini=1−∑pi2,其中 p i {p_{i}} pi 表示类 i {i} i 的数量占比
决策树的生成过程就是让熵或基尼指数最小化的过程,基本步骤为:
步骤1:将所有的数据看成是一个节点,进入步骤2;
步骤2:从所有的数据特征中挑选一个数据特征对节点进行分割,进入步骤3;
步骤3:生成若干孩子节点,对每一个孩子节点计算其熵或基尼指数,如果满足条件,进入步骤4;否则,进入步骤2;
步骤4:设置该节点是子节点,其输出的结果为该节点数量占比最大的类别。
随机森林是基于决策树的,就像我们买鞋子时,也会听好朋友们的建议,我们的每个好朋友就是一棵决策树,每一个好朋友可能会给出不同的建议,我们自己则会根据所有的好朋友的建议和自己的感觉综合决定是否购买。这就是森林,由很多颗决策树所构成,最终答案取森林的众数。
而随机森林就是比森林多了一个“随机”,这个“随机”体现在以下两个方面:
1、对于每一颗决策树的训练样本,采取随机有放回抽样得到。
2、对于每一颗决策树所使用的特征,采取随机不放回抽样。
这两步又称为:bootstrap。简言之,bootstrap的目的就是尽量使每一颗决策树的训练样本和训练特征不尽相同。
那么,这么做有什么好处呢?答案是显而易见的,如果每颗树用的训练集都差不多,那么每棵树其实也就长的差不多,就失去了森林的意义了。
好了,至此,决策树和随机森林就讲完了,我们在这里不必深究它的具体实现,只需要知道大体这个概念即可,因为 sklearn 中有写好的算法,我们只需要会使用即可。
二、算法实现
这里笔者采用兵王问题,详细规则介绍见链接 兵王问题规则介绍 。如果需要数据集,请 点击下载 提取码: 67je 。
1、导入数据
import graphviz
import pandas as pd
from sklearn import tree
from sklearn import model_selection
from sklearn import ensemble
# 载入数据
data = pd.read_csv("krkopt.data", ',')
2、进行数据初步处理
# 为每一列数据贴上标签
data.columns = ["wx", "wy", "wwx", "wwy", "vx", "vy", "outcome"]
# 进行数据的初步处理,将 a-h 用 1-8 替换,draw 表示和棋用 1 替换,非 draw 表示一方赢兵王赢,用 0 替换
data.replace(to_replace={'^a$': 1, '^b$': 2, '^c$': 3, '^d$': 4, '^e$': 5, '^f$': 6, '^g$': 7,
'^h$': 8, '^draw$': 1, "(?!draw)": 0}, regex=True, inplace=True)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(
data[['wx', 'wy', 'wwx', 'wwy', 'vx', 'vy']], data['outcome'], train_size=0.7
)
del data
3、创建决策树
# 创建决策树对象
clf = tree.DecisionTreeClassifier()
# 开始构建决策树
clf.fit(X_train, y_train)
# 查看测试集正确率
print("正确率为:", clf.score(X_test, y_test))
实际上拥有很多参数,这里给出参数详解,读者自行修改参数,观察效果。
参数详解:
1.criterion:{“gini”, “entropy”}, default=”gini”
决策树所使用的划分指标目标函数
2.splitter:{“best”, “random”}, default=”best”
“best” 是在所有特征中找最好切分点,让决策树的目标函数达到最小,即寻找一棵最优决策树,非常耗时。
“random” 是随机在特征中寻找切分点,所得的决策树可能不是最优,但也不会差,适合数据量特别大或要使用随机森林的时候
3.max_depth:int, default=None
限制决策树的最大深度,None为无限制
4.min_samples_split:int or float, default=2
限制结点划分的最小样本数,int 为绝对数量,float 为所占样本比例(向下取整)
即若某结点样本数少于 min_samples_split 时,就不继续对该结点进行划分
5.min_samples_leaf:int or float, default=1
限制叶子结点的最少样本数,int 为绝对数量,float 为所占样本比例(向下取整)
即若某结点划分后所得叶子节点的样本数 少于 min_samples_leaf 时,就不对该结点进行此次划分
6.min_weight_fraction_leaf:float, default=0.0
限制叶子结点的最小权重总和,有了权重之后,样本量就不再是单纯地记录数目,而是受输入的权重影响了,
注意,基于权重的剪枝参数(例如 min_weight_ fraction_leaf、class_weight)可以让决策树偏向于某一些类别
7.max_features:int, float or {“auto”, “sqrt”, “log2”}, default=None
在生成决策树时所使用的特征数量
None为使用全部特征,int 为绝对数量,float 为所占特征比例(向下取整)
auto 和 sqrt 是一样的,即 max_features=sqrt(n_features)
log2 即 max_features=log2(n_features)
8.max_leaf_nodes:int, default=None
限制决策树叶子节点的最大数量,可有效防止过拟合,None 为无限制
9.min_impurity_decrease:float, default=0.0
限制决策树划分的最小不纯度下降值,若某个结点划分后所带来的不纯度下降量小于等于 min_impurity_decrease 就不进行此次划分
10.min_impurity_split:float, default=1e-7
限制划分的最小不纯度,如果某个结点的不纯度(criterion的值)小于 min_impurity_split 就不对该结点进行划分
11.class_weight:dict, list of dict or “balanced”, default=None
指定样本各类别的权重,让决策树更偏向于某些类别
3、可视化查看决策树
#%% 将得到的决策树保存,以供可视化查看
with open("二手车交易价格预测/tree.dot", 'w') as f:
tree.export_graphviz(clf, f)
在命令行窗口,切换到 D:\ProgramData\Anaconda3\envs\TF2.1\Library\bin\graphviz(前面的路径是自己的 Anaconda 安装路径)
如果没有这个路径,请先安装 graphviz 包
输入:dot -Tpng D:\tree.dot -o D:\tree.png
即可查看最后的决策树
4.、创建随机森林
clf = ensemble.RandomForestClassifier(n_estimators=200, bootstrap=True, oob_score=False, n_jobs=5)
# 开始创建随机森林
clf.fit(X_train, y_train)
# 观察预测正确率
print(clf.score(X_test, y_test))
print(clf.feature_importances_)
决策树的参数都可以用到随机森林,这里就只介绍随机森林独有的参数
1.n_estimators:integer, optional (default=100)
要创建的树的数量
2.bootstrap:boolean, optional (default=True)
是否进行 bootstrap
3.oob_score:bool (default=False)
是否进行包外估计(out-of-bag estimate):用未在训练集中出现的测试数据来作出决策,
包外样本来辅助剪枝,或用于估计决策树中各结点的后验概率以辅助对零训练样本结点的处理。
4.n_jobs:int or None, optional (default=None)
要开几个进程来进行操作(多进程可大大提高 cpu 利用率,缩短训练时间)