数据挖掘-理论与算法 公开课笔记
数据挖掘-理论与算法 公开课笔记
制作:纪元
本提纲遵循CC-BY-NC-SA协议
(署名-非商业性-相同方式共享)文章目录
- 10.2.1.1 Data Cleaning 数据清洗
- 11.2.2.1 Outliers & Duplicate detection 异常值与重复检测
- 12.2.3.1 Type conversion & sampling 类型转换与采样
- 14.5.2.1 Feature Selection 特征选择
- 15.2.6.1 Feature Extraction 特征提取
- 16.2.7.1 The Issue of PCA PCA存在的问题以及解决
- 16.2.7.2 LDA Example 线性判别分析例
- 19.3.1.1 Bayes、Decision Tree 贝叶斯、决策树(概率基础)
- 20.3.2.1 Naive Bayes Classifier 朴素贝叶斯公式
- 21.3.3.1 Decision Tree 决策树
- 22.3.4.1 Decision Tree Framework 决策树的建立策略
- 24.4.1.1 Perceptrons 感知机
- 25.4.2.1 感知机的应用
- 26.4.3.1 Multilayer Perception 多层感知机神经网络
- 27.4.4.1 分类器学习算法
- 28.4.5.1 Beyond BP Networks 其他的神经网络算法
- 30.5.1.1 Support Vector Machine(SVM) 支持向量机
- 31.5.2.1 Linear SVM 线性SVM
- 32.5.3.1 Non-linear SVM 非线性SVM
- 33.5.4.1 SVM Roadmap SVM发展历史
- 34.5.5.1 Clustering 聚类
- 36.6.2.1 Clustering Algorithm聚类算法
- 37.6.3.1 EM Method 期望最大法
- 38.6.4.1 Density/Hierarchical Based Methods 密度与层次
- 39.7.1.1 Assocation Role 关联规则
- 40.7.2.1 Support&Confidence of Association Role 支持度 置信度
- 41.7.3.1 About Assocation Role 关联规则的误区
- 42.7.4.1 Apriori Method Apriori算法
- 44.7.6.1 Sequential Pattern 序列模式
- 46.8.1.1 Recommend Algorithm 推荐算法
- 47.8.2.1 Text Analysis 文本分析
- 48.8.3.1 PageRank 网页评分
- 49.8.4.1 Collaborative Filtering 协同过滤
- 51.9.1.1 Ensemble Learning (1) 集成学习(1)
- 52.9.2.1 Ensemble Learning (2) 集成学习(2)
- 53.9.3.1 Ensemble Learning (3) 集成学习(3)
- 56.10.1.1 Evolutionary Algorithms 进化算法
- 57.10.2.1 Objective Function 目标函数
- 59.10.4.1 Genetic Algorithm(1) 遗传算法-初探(1)
- 60.10.5.1 Genetic Algorithm(2) 遗传算法-框架(2)
- 60.10.5.1 Genetic Algorithm(3) 遗传算法-可能性(3)
- 62.10.6.1 Genetic Algorithm(4) 遗传算法-遗传程序(4)
- 63.10.7.1 Genetic Algorithm(5) 遗传算法-遗传硬件(5)
10.2.1.1 Data Cleaning 数据清洗
数据在获得时可能并不可用,缺数据,数据错误,噪音等问题都会导致程序无法运行。因此在处理之前要进行清洗等操作
对于缺失少量的数据,可以进行适当的推测,或者规则界定,或者直接填均值,这个方向主要由经验主导。
离群点和异常点是有区别的,要谨慎的区分两者。
11.2.2.1 Outliers & Duplicate detection 异常值与重复检测
异常是相对的,在计算异常值时要考虑相对性,可以尝试与近邻值相比较。
相同的信息可以用不同的形式来表示。而计算机可能无法识别这些重复。
我们可以尝试使用滑动窗口,将某数据与部分之前的数据进行比(前提是相似的数据是紧邻的)
12.2.3.1 Type conversion & sampling 类型转换与采样
数据有很多形式,在编码时需要选择合适的方式进行处理,才能进行数据挖掘。
在编码时,编码不同方式对问题结构和挖掘结果都会产生影响。
采样:数据并不是都需要的,而且IO操作对数据库并不友好,我们可以根据需要可以进行适当的采样,能有效的降低数据量,加快处理速度。
不平衡的数据集对挖掘结果也会有影响,在采样时也需要谨慎选择(可以尝试“复制”一些较少点加入数据集)。
在做分类的情况下,当数据过多时,也可以尝试识别出边缘点并进行加入数实验据集,可以有效地降低实验时的数据量。
14.5.2.1 Feature Selection 特征选择
在做数据挖掘的时候,要在多个属性中进行挑选,否则会影响算法的效率与资源的消耗,所以属性分好坏
熵-(Entropy):在数据挖掘中,代表变量/系统的不确定性。
- H ( x ) = ∑ i = 1 n p ( x i ) l o g b p ( x i ) H(x)=\sum\limits_{i=1}^n p(x_i)log_bp(x_i) H(x)=i=1∑np(xi)logbp(xi) 此处b一般取2,但也可以为其他值,取2时单位为比特
信息增益-(information gain):在数据挖掘中代表属性的价值
- Δ H ( x ) = H ( x 1 ) − H ( x 2 ) \Delta H(x)=H(x_1)-H(x_2) ΔH(x)=H(x1)−H(x2) 即增加属性前后熵的差值
属性组的优劣并不是单纯的单个属性好坏的叠加,因为属性间可能有影响或者关联。
搜索最优属性-(Subset Seach):为了在众多属性中挑选最优的属性组,会有众多的排列组合,所以需要通过适当的算法。
Branch and Bound:寻找最优的属性组。建立属性树,如有单调的情况,可以通过剪枝方法加速。启发式、模拟退火等算法同样适用
15.2.6.1 Feature Extraction 特征提取
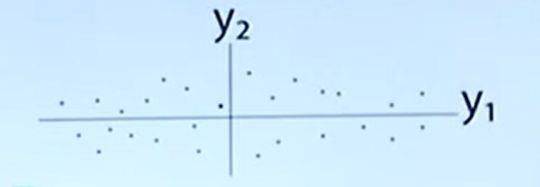
引例:照片把三维信息压缩(投影)为二维,信息损失很多,人们通过照片的特征,依旧可以识别照片中的物体。
不同的属性有不同的区分度,越重要的属性越能区分物体,更少产生重复。所以属性有好坏
此图(理想情况下)中属性 Y 2 Y_2 Y2劣于属性 Y 1 Y_1 Y1(不能更好的区分数据点)我们将数据点向x轴投影,丢失的就是y轴方向的信息
主成分分析技术-PCA(principle components analysis):把坐标平面的点向坐标轴投影,相当于降维,投影方向(相当于属性)有好坏。最优情况为最大特征向量。
数学工具:拉格朗日数乘法
实际情况下,数据的属性往往有联系,此时要将图像移动、并旋转到理想情况。
16.2.7.1 The Issue of PCA PCA存在的问题以及解决
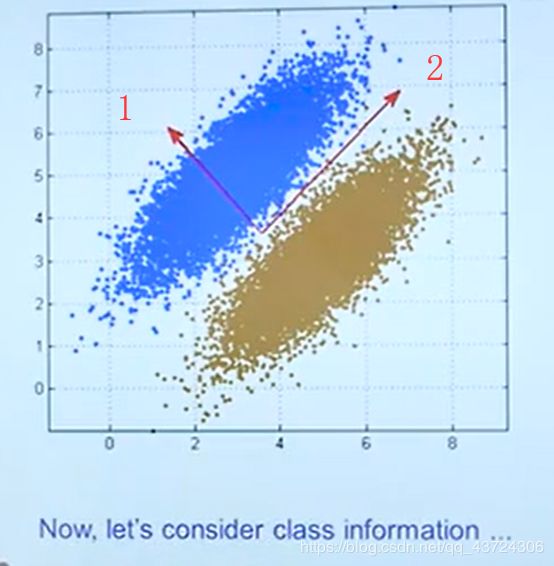
PCA是一种无监督学习,虽然可以进行降维,但是在分类时,PCA可能无法进行合理的投影方向选择,导致无法进行分类。
举例:如果向1轴投影,可以明显区分两个数据集,但是PCA会向2轴投影,导致两个数据在低维混合,看不出分类。
线性判别分析-LDA(Liner Discriminant Analysis):相对PCA,LDA在投影的同时保留类的区分信息(指相同组中数据尽可能近,不同组中数据尽可能远)
费舍尔准则-(Fisher Criterion):用于评估投影效果好坏(整体上越大越好)
- J = ∣ ( μ 1 − μ 2 ) 2 S 1 2 + S 2 2 ∣ J=|\frac{(\mu_1-\mu_2)^2}{S_1^2+S_2^2}| J=∣S12+S22(μ1−μ2)2∣ 其中 μ \mu μ为组中心点位置(越远越好), S S S为各组离散程度(越小越好)
16.2.7.2 LDA Example 线性判别分析例
LDA不仅仅局限于二分类,可以容易的拓展到 n n n类的情况,此时 J J J的分子为各个组中心点离所有点中心点的距离。此时 n n n分类最高可以投影到 n − 1 n-1 n−1维上
在一些特殊情况下(两类比较近或者两个分类维互相垂直),LDA的分类可能不如PCA,在使用时要谨慎分析。
19.3.1.1 Bayes、Decision Tree 贝叶斯、决策树(概率基础)
分类是一种有监督学习,会有标签,这也是分类与聚类的差别。
数学工具:贝叶斯公式
20.3.2.1 Naive Bayes Classifier 朴素贝叶斯公式
注意区分:先验后验、相关独立
拉普拉斯平滑-(Laplace Smoothing):如果出现数据库中从未存储的特殊点,一项为0会导致整个概率公式值为0。
- P ( a j k ∣ ω i ) = ∣ ( a j = a j k ) ∧ ( ω = ω i ) ∣ + 1 ∣ ω = ω i ∣ + ∣ a j ∣ P(a_{jk}|\omega_i)=\frac{|(a_j=a_{jk})\land(\omega=\omega_i) |+1}{|\omega=\omega_i|+|a_j|} P(ajk∣ωi)=∣ω=ωi∣+∣aj∣∣(aj=ajk)∧(ω=ωi)∣+1(加1导致不会为0)
贝叶斯公式的实际应用:
我们可以提取文章中的部分单词,根据出现与否计算文章分类概率,但是这种情况会导致计算量非常大。改进 词袋模型-(Word Bag),根据单词在文章中出现的频率来计算文章分类概率。
21.3.3.1 Decision Tree 决策树
将不同因素设定规则,分层计算,形成决策树。决策树是可解释的(if…then…),是决策树的一大优势
根据判断顺序不同,一个数据集可以建立很多树。运用奥卡姆剃刀,我们可以选择同样分类效率下,尽量简单的决策树,
22.3.4.1 Decision Tree Framework 决策树的建立策略
此章有拓展资料
把分类能力强的节点放在靠近根节点的情况可以大大缩小树的规模,于是决策树的建立与属性判断有关
熵-(Entropy):在变量选择中,代表属性的不确定性。最大值为1,此时最不确定。最小值为0,此时最确定。
- E n t r o p y ( S ) = − ∑ i = 1 C p i l o g b ( p i ) Entropy(S)=-\sum\limits_{i=1}^C p_ilog_b(p_i) Entropy(S)=−i=1∑Cpilogb(pi) 此处b一般取2,但也可以为其他值,取2时单位为比特
过学习-(Overfitting):在训练集中a比b效果好,但在测试集中b比a好,此时就发生了过学习(通用概念)
决策树并不是越大越好,也存在过学习(overfitting)的情况。为避免过学习,有两种剪枝策略:
- 限制树的深度
- 进行剪枝(将某些子节点合并到父节点上)
简单的决策树 ID3 建立过程:
- 寻找能把数据集分的最开的属性,进行分割
- 如果子集纯,那么停止分割,如果不纯,继续从1分割(如果没有属性,停止分割,标签少数服从多数)
24.4.1.1 Perceptrons 感知机
神经网络是计算机程序对大脑中神经元的简化抽象模拟。
单个神经元开关速度(0,1互换)相对计算机比较慢,但人脑是多个神经元联合分布式处理的,处理速度很快。
感知机-(Perceptrons):单个的神经元,n个输入,n+1个权重( w 0 w_0 w0,避免所有点都过原点),输出0或1
25.4.2.1 感知机的应用
感知机可以理解为一个线性分类器,对于线性不可分等问题无能为力
梯度下降法-(Gradient Descent):取权重时不同权重对结果影响不同,所以让误差不断梯度下降
批处理学习-(Batch Learning):计算一批数据,将更改值保存在 Δ w \Delta w Δw中,计算完后统一修改 w w w
随机学习-(Stochastic Learning):一旦出现误差,就修改 w w w
26.4.3.1 Multilayer Perception 多层感知机神经网络
多层感知机通过在输入和输出间添加隐层来提升效率
多次感知机解决线性不可分问题:将输入的线性不可分问题转化为线性可分问题,输出到隐层,由隐层解决并输出。
27.4.4.1 分类器学习算法
误差反向传播算法-BP(Backpropagation Rule):思想类似于感知机,用误差对某个权重的输入求偏导。但在多层感知机网络中,由于隐层的期望值并不知道,所以没法得知隐层的误差,因此输出后根据结果加权反向反馈,修改参数。
在求导时,很容易使参数掉进局部最优点,导致误差不在下降,而神经网络恰恰有很多局部最优点。为了解决这个问题,
- 我们可以尝试多次从不同点、不同方向出发,寻找最优参数。
- 也可以增加“冲量”,相当于“惯性”,让参数点冲过一些比较小的局部最优点。
- 也可以尝试改变学习率,较大的学习率可以直接大踏步跳过一些比较小的局部点,
- 而特殊的学习率会在一些特殊情况产生震荡,左右横跳导致无法收敛,多次学习也是解决办法。
同样,神经网络也有过学习问题。所以我们既要设置训练误差-(Training Error)—–随时间逐步降低,又要设置校验误差-(Validation Error)—–随时加先降后升。在校验误差拐点停止训练即可。
28.4.5.1 Beyond BP Networks 其他的神经网络算法
此章有拓展资料
Elman Network:此算法有一定的记忆性,通过之前的输入推出答案,输出不仅仅取决于当前的输入,还取决于之前的输入。
Hopfield Network:是一个全连接神经网络。类似于人大脑的记忆功能,利用收敛到局部最小值,实现联想记忆。
同样,不存在万能的神经网络,每个网络算法都有自己的适应性,而且神经网络的训练时间很长,但训练完成后反应很快。
神经网络的可解释性很差(只有权重)
30.5.1.1 Support Vector Machine(SVM) 支持向量机
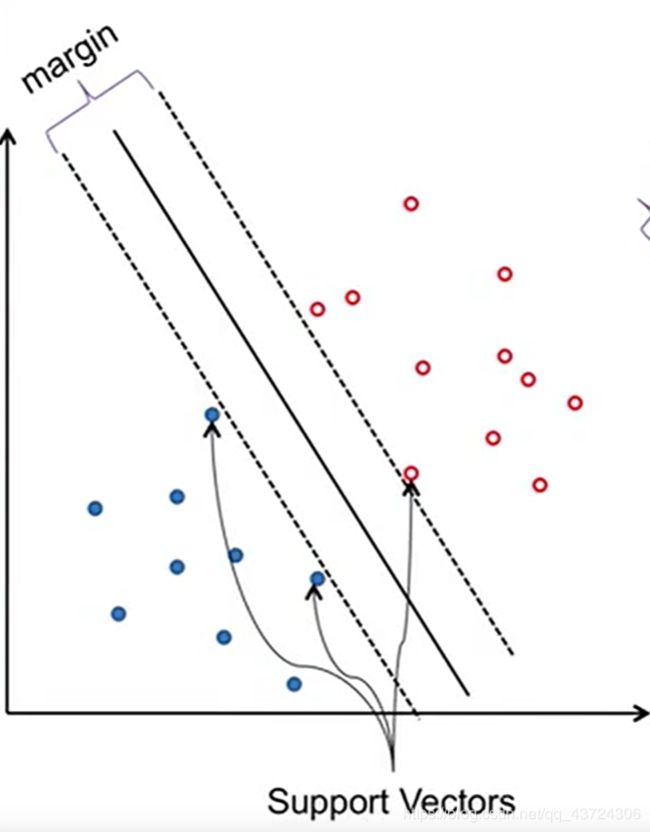
原理:输入维度向高维映射并进行分类(升维),仍然是线性分类器的一种,真正有效的点只有support vector。
边缘-(margin):训练集中分界面可以上下平移的区域,margin越大,错误越不会影响结果,参数越好。
支持点-(Support Vectors):导致平移边界的点,决定了分界面能移动的范围。
31.5.2.1 Linear SVM 线性SVM
目标:先分样本(必须分对所有的点),再求最优值
数学工具:拉格朗日乘数法
但事实上很难完美的分对所有点,所以放宽条件(soft margin),允许少数点可以不满足约束条件。
本质上还是一个线性分类器,仍然无法解决线性不可分问题。(soft margin只能解决数据有噪点的情况)
32.5.3.1 Non-linear SVM 非线性SVM
目的:弥补线性SVM不能解决线性不可分问题的缺陷
原理:输入坐标点向新坐标空间映射并进行分类,可以是升维,也可以是同维度转化。
映射方法一般是固定的,m维一般升到 m 2 2 \frac{m^2}{2} 2m2维进行分类。
通过引入核函数进行等价变换,让高维空间的计算等价于低维空间的运算,有效降低运算量。
在处理文本数据时,可以使用字符串核函数,处理字符串的子串,得到相应的式子进行分类。
33.5.4.1 SVM Roadmap SVM发展历史
此章有拓展材料
SVM理论体系的形式不是一蹴而就的,而是经过了不断地优化改善。
线性分类器-(让margin最大化)-线性SVM-(解决数据存在噪声问题)-soft margin-(解决线性不可分问题)-向高维映射-(解决计算复杂度过高问题)-引入核函数
模型能力指数(model capacity):若h个点无论怎么打标签,模型都能区分(shatter),那么该模型能力指数就是h
模型复杂性和风险相关,一般越复杂的模型风险越高。
34.5.5.1 Clustering 聚类
相似性导致聚集,聚类有两种:分割型聚类(将数据进行分块),层次型聚类(根据不同层次分块)
聚类是无监督学习,没有人打标签,没有绝对标准答案。
目的:使不同簇(clusters)之间距离最远,相同簇最近
数据预处理对聚类影响很大,要谨慎对待。
36.6.2.1 Clustering Algorithm聚类算法
Silhouette:衡量聚类效果的参数,一般在[0,1)间,也存在少数负数
- S ( i ) = b ( i ) − a ( i ) m a x { b ( i ) , a ( i ) } S(i)=\frac{b(i)-a(i)}{max\{b(i),a(i)\}} S(i)=max{b(i),a(i)}b(i)−a(i)
K-Means算法:
- 要分n块,则随机选n个种子点(模型参数)
- 根据n个点将数据域划分
- 计算数据域的中心点,更新为种子点,循环到1步
优点:对“球形”数据效果好,收敛快(一般5,6步能出结果)
缺点:K值难以不确定,初始点不好可能导致陷入局部最优点,噪点影响大,对“异型数据”适应性不好
最终目的:求出把数据域分成n块的n个中心点(参数)
Sequential Leader Clustering算法:
可以应对数据流进行聚类,且不需要迭代,一遍过,且不需要确定K。
进来的数据,根据设定距离极限,直接与现有中心点距离进行比较,大于则自成中心,小于则加入簇中。
对于距离限设定比较敏感,太小则会产生很多簇,太大簇又会过少。
37.6.3.1 EM Method 期望最大法
混合高斯模型-(Gaussian Mixture):用不同高斯分布进行叠加,每个分布都有相应权重 ( α i ) (\alpha_i) (αi),权重和为1。
- g ( x , μ , σ ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 g(x,\mu,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} g(x,μ,σ)=2πσ21e−2σ2(x−μ)2 高斯分布
- F ( x ) = ∑ i = 1 n a i g ( x , μ i , α i ) , α i ≥ 0 & ∑ i α i = 1 F(x)=\sum\limits_{i=1}^na_ig(x,\mu_i,\alpha_i),\alpha_i\geq0\&\sum\limits_{i}\alpha_i=1 F(x)=i=1∑naig(x,μi,αi),αi≥0&i∑αi=1
期望最大化算法-EM:类似于K均值聚类,先随机生成各参数,再通过不断迭代进行训练,调整参数。
38.6.4.1 Density/Hierarchical Based Methods 密度与层次
此章有拓展材料
为了解决“非规则分布”数据和“大噪声”数据的问题,从密度方向解决问题
优点:不需要设定K值或距离极限(虽然还要定义一个距离参数)
DBSCAN算法:通过点与点之间的距离进行聚类,不断递归膨胀,其中距离参数即为分类的层面,越小的话分类层析越低,越大分类层次越高。
核心点:在一定距离(需要用户设定)内有足够的点
边缘点:在核心点距离范围内且不是核心点的点
噪点:既不是核心点也不是边缘点(需要排除)
Hierarchical Based Methods:算模型中每个点与其他点的距离矩阵,选模型中最近的两个点合并进一个簇,迭代至只有一个簇结束。
最小距离法:合并后新簇与其他簇的距离,为两簇中距离最小的点之间的距离
最大距离法:合并后新簇与其他簇的距离,为两簇中距离最大的点之间的距离
39.7.1.1 Assocation Role 关联规则
目的:在庞大的元素库中找出元素之间的关联关系
这个规则主要应用在商品的推销上(啤酒与尿布)
还可以延伸用于文字分析,把单个单词看做元素,对每篇文章分析即可得出单词之间的关联关系
40.7.2.1 Support&Confidence of Association Role 支持度 置信度
支持度在关联规则分析中就是频率( 关 联 发 生 的 次 数 总 次 数 \frac{关联发生的次数}{总次数} 总次数关联发生的次数)
置信度为在某元素出现的情况下关联发生的概率( 关 联 发 生 的 次 数 包 含 某 一 元 素 的 次 数 \frac{关联发生的次数}{包含某一元素的次数} 包含某一元素的次数关联发生的次数)即条件概率
- S u p p o r t ( X → Y ) = # ( X ∪ Y ) n Support(X\rightarrow Y)=\frac{\#(X\cup Y)}{n} Support(X→Y)=n#(X∪Y)
- C o n f i d e n c e ( X → Y ) = # ( X ∪ Y ) # X Confidence(X\rightarrow Y)=\frac{\#(X\cup Y)}{\#X} Confidence(X→Y)=#X#(X∪Y)
注意规则顺序,顺序相反分母会变化,Confidence也会变化
在大元素集中,组合的数量会快速增加,同时记录也是海量的,一条一条验证显然不可行。·
宏观处理:
- 设置一个支持度、置信度的一个限值
- 把所有频繁的组合找出来
- 生成频繁组合的所有非空子集,并写出所有可能的子集关联规则
- 计算所有子集关联规则的支持度与置信度
- 比较子集的支持度、置信度与设定的限值,若超过则认为关联性强
41.7.3.1 About Assocation Role 关联规则的误区
规则的关联性很强并不一定代表该规则有意义(当两个元素频率差别特别大时尤为明显)
关联规则就是一个条件概率,两件事物相关,并不一定他们之间有代表因果关系,不应做过多解释。
42.7.4.1 Apriori Method Apriori算法
元素因为排列组合,所有可能的非空关联的数量非常庞大 ( 2 d − 1 ) (2^d-1) (2d−1),不能用传统方法解决。
原理:
- 任何一个频繁项的子集必须频繁
- 如果某个规则不频繁,那么他的超集必须不频繁
相当于一个剪枝算法
具体步骤:
- 生成某个特定大小的频繁集(一般为1)
- 对频繁集进行组合,并删除频繁集
- 迭代运行1,2
核心思想:尽量避免生成不频繁集
缺点:本算法需要频繁扫描数据库,而这种操作在大型数据库中成本较高
44.7.6.1 Sequential Pattern 序列模式
此章有拓展材料
在一般的记录中,不包含记录产生的时间或者购买人,那么对于序列先后或间隔的分析就无法进行。
目的:分析某事发生后,另一件事就有可能发生
我们将序列按先后时间排序,若某 元素顺序 持续在序列集中出现,那么该 元素顺序 就是一个序列(不一定要直接连续,允许有间隔)
方法:先找短序列,不断连接变为长序列,并检验是否频繁即可。
46.8.1.1 Recommend Algorithm 推荐算法
应用:精准广告营销、协同推荐、音乐推荐
47.8.2.1 Text Analysis 文本分析
Tf-idf:输入关键词,量化该词与数据库词中的关联情况
关键词频率-TF(Term Frequency):关键词的频率
逆文档频率-(Inverse Document Frequency):该单词在其他文档中的频率(作用:过滤诸如“the”“a”之类的词)
单词-文本矩阵-(Term-Document matrix):在文本处理时,将单词和多个文本的tf-idf值组成矩阵并进行计算
-
t f ( t , d ) = n t , d ∑ k n k , d tf(t,d)=\frac{n_{t,d}}{\sum_kn_{k,d}} tf(t,d)=∑knk,dnt,d( 某 词 在 全 文 中 出 现 的 频 数 全 文 词 总 频 数 \frac{某词在全文中出现的频数}{全文词总频数} 全文词总频数某词在全文中出现的频数)
-
i d f ( t , D ) = l o g ∣ D ∣ ∣ { d ∈ D : t ∈ d } ∣ idf(t,D)=log\frac{|D|}{|\{d\in D:t\in d\}|} idf(t,D)=log∣{d∈D:t∈d}∣∣D∣( l o g 所 有 文 档 个 数 包 含 特 定 词 文 档 个 数 log\frac{所有文档个数}{包含特定词文档个数} log包含特定词文档个数所有文档个数)
-
t f − i d f ( t , d , D ) = t f ( t , d ) × i d f ( t , D ) tf-idf(t,d,D)=tf(t,d)\times idf(t,D) tf−idf(t,d,D)=tf(t,d)×idf(t,D)
在计算机处理文档时,一般将文章处理为向量并进行计算夹角。
在文档处理时,近义词(Synonymy)、多义词(Polysemy)的存在会干扰文档处理。
隐含语义分析-LSA(Later Semantic Analysis):将矩阵放进新的空间而不是原空间进行分析
- X = T S D − 1 X=TSD^{-1} X=TSD−1 S:对角阵
- 将 X X X分解为 T S D − 1 TSD^{-1} TSD−1
- 选择几个信息量最大的维度并进行降维
- 将降维后矩阵乘回去并画图
- 对新得的图进行聚类
48.8.3.1 PageRank 网页评分
页面评分-(PageRank):网页可以被看为互相有链接的文档,其PageRank值越高代表网页越好。
指向某网页的链接越多、指向来源的PR值越高、指向来源的指向链接越少,某网页质量越高。
- P R ( P i ) = ∑ p j ∈ M ( p i ) P R ( p j ) L ( p j ) PR(P_i)=\sum\limits_{p_j\in M(p_i)}\frac{PR(p_j)}{L(p_j)} PR(Pi)=pj∈M(pi)∑L(pj)PR(pj) 即: 来 源 网 站 P R 值 来 源 网 站 的 链 接 数 \frac{来源网站PR值}{来源网站的链接数} 来源网站的链接数来源网站PR值之和
- P R ( P i ; t + 1 ) = 1 − d N + d ∑ p j ∈ M ( p i ) P R ( p j ) L ( p j ) PR(P_i;t+1)=\frac{1-d}{N}+d\sum\limits_{p_j\in M(p_i)}\frac{PR(p_j)}{L(p_j)} PR(Pi;t+1)=N1−d+dpj∈M(pi)∑L(pj)PR(pj) 即:t+1秒时网站的PR值,是一个迭代值,最终收敛为定值
- d-阻尼参数(damping factor):固定参数,一般取0.85
- 1 − d N \frac{1-d}{N} N1−d是让所有时间所有网页PR值和为1
49.8.4.1 Collaborative Filtering 协同过滤
核心思想:收集兴趣相似的用户的打分信息,并制作打分矩阵,表示并推测每个人对每个商品的喜爱程度。
既可以在用户间计算关联,也可以在商品之间计算关联,也可以建立模型进行计算,在不同情况下采用的算法也不一样。
可能影响算法的因素:
- 灰羊效应:即介于黑白之间的情况
- 冷启动:用户新来平台,没有数据,如何推荐
- 网络水军的故意攻击
- 用户的打分习惯(有人习惯打高分,有人习惯打低分,因此要与平均分进行计算)
51.9.1.1 Ensemble Learning (1) 集成学习(1)
核心思想:有策略的集中不同类型的分类器,根据综合结果得出结论。
也可以对模型进行拆分,将复杂的问题拆成简单的问题来解决。本质上是分类器的实用策略
52.9.2.1 Ensemble Learning (2) 集成学习(2)
在集成学习中,集中策略可以使用“少数服从多数”或“权重”来决定最终决策走向,且不用担心过学习问题。
为了保证各个分类器结论相似而不同,可以使用不同部分的数据集来训练每个分类器。
引导聚集算法-Bagging(Bootstrap Aggregating):
- 将数据集用bootstrap法采样为若干子数据集
- 在子数据集上训练分类器
- 用这些分类器处理数据,根据结果“少数服从多数”得出答案
未选入子数据集的数据(OOB-Out Of Bag,大约 1 3 \frac{1}{3} 31)可以用来检验。
53.9.3.1 Ensemble Learning (3) 集成学习(3)
每个分类器分类效果不同,每个数据集容易被分对的可能性也不同,他们所占的权重也不应该相同,这里的权重也可以学习。
Stacking算法(并行):在原始的分类器(学习输出结果)输出基础上,再过一层分类器(学习各个分类器的权重),从而得出最终结果。可以视为Bagging的升级版。
Boosting算法(串行):先训练一个分类器,对于分对的和分错的分开划分数据集,针对正误数据集进行继续训练(相当于对训练集加权重,越多分类器分错,该数据集权重越大)
56.10.1.1 Evolutionary Algorithms 进化算法
进化算法的目的:
- 优化(广义的)
- 进行模拟,帮助人类理解自然的进化
特点:
- 基于数量的
- 有随机性
- 并行(不易局部最优)
- 适者生存
- 不局限于某种特定问题,可能是普适的
- ……
57.10.2.1 Objective Function 目标函数
机器学习算法本质还是优化问题,只不过有难有易。
现实中的大部分问题都是复杂的,很难直接暴力解决,必须要进行优化。
59.10.4.1 Genetic Algorithm(1) 遗传算法-初探(1)
遗传算法是松散的基于达尔文进化论,并不是完全相同的。
遗传算法的几部分:表示(二进制还是格雷码等)、遗传、选择、变异、表达(向量)
格雷码与二进制的区别:系统在每一次变化时,码值只会变化一位,更加稳定。
在设置权重的时候,可以用原始值比例确定,也可以用序号确定(防止过于优秀的个体占据了过大概率)
在选择时,可以两两PK选择,可以精英选择(防止突变导致的结果不稳定),可以用百分率选择
60.10.5.1 Genetic Algorithm(2) 遗传算法-框架(2)
杂交:尝试生成更多的可能
- 一点杂交:只选择一个点,将点后的段交换
- n点杂交:选择n个点,在点与点之间的片段进行交换
变异:保证多元基因的存在,防止收敛到只有一个物种(变异率不应太高)
选择:给更适应的个体更大概率
基本框架(两层循环):
- 生成种群
- 代际循环
3. 代内循环
60.10.5.1 Genetic Algorithm(3) 遗传算法-可能性(3)
遗传算法在维度过大时复杂度会比较高,要进行适当的选择。
遗传算法在分类和聚类中均可以应用,
Pareto Front:在多目标优化的情况下,基于不同的评判角度无法选择最优点,此时交给用户选择。
62.10.6.1 Genetic Algorithm(4) 遗传算法-遗传程序(4)
**遗传算法-(Genetic Algorithm)与遗传程序-(Genetic Program)**的区别:遗传算法输出的是模型参数,遗传程序输出的则是一段计算机程序
遗传程序将计算式表示为树,针对树进行杂交进行优化,一模一样的树在杂交后也能产生新树。
评判方式:用积分计算目标值与当前值之间差异部分的面积,面积大则拟合性不好。
63.10.7.1 Genetic Algorithm(5) 遗传算法-遗传硬件(5)
可计划电路-(Evolvable Circuits):硬件的线路可以变化并改变结构,实现原先没有的功能。
用途:
- 芯片在遇到设计时未想到的情况时,能自行修整并应对环境。
- 设计天线形状达到最优性能
- 汽车的外形设计
- ”人工生命“
- 程序绘画、谱曲
困难的地方:对于运行结果的评价是难以量化并打分的,可能需要人类的评判