python123练习5: 函数和代码复用 (第5周)
实例7:七段数码管绘制
描述
这是"实例"题,与课上讲解实例相同,请作答检验学习效果。
七段数码管是一种展示数字的有效方式。
请用程序绘制当前系统时间对应的七段数码管,效果如下:

要求如下:
(1) 使用 time 库获得系统当前时间,格式如下:20190411
(2) 绘制对应的七段数码管
(3) 数码管风格不限
请在本机编写代码完成实例,建议有趣的风格请在Python123的绘图专区上传展示。
import turtle as t
import time
def drawGap(): #绘制数码管间隔
t.penup()
t.fd(5)
def drawLine(draw): #绘制单段数码管
drawGap()
t.pendown() if draw else t.penup()
t.fd(40)
drawGap()
t.right(90)
def drawDigit(d): #根据数字绘制七段数码管
drawLine(True) if d in [2,3,4,5,6,8,9] else drawLine(False)
drawLine(True) if d in [0,1,3,4,5,6,7,8,9] else drawLine(False)
drawLine(True) if d in [0,2,3,5,6,8,9] else drawLine(False)
drawLine(True) if d in [0,2,6,8] else drawLine(False)
t.left(90)
drawLine(True) if d in [0,4,5,6,8,9] else drawLine(False)
drawLine(True) if d in [0,2,3,5,6,7,8,9] else drawLine(False)
drawLine(True) if d in [0,1,2,3,4,7,8,9] else drawLine(False)
t.left(180)
t.penup()
t.fd(20)
def drawDate(date):
t.pencolor("red")
for i in date:
drawDigit(eval(i))
def main():
t.setup(800, 350, 200, 200)
t.penup()
t.fd(-300)
t.pensize(5)
drawDate(time.strftime('%Y%m%d',time.gmtime()))
t.done()
main()
基本思路:
步骤 1:绘制单个数字对应的码管
步骤 2:获得当前系统时间,变成字符串,绘制对应的码管
思维方法:
-模块化思维:确定接口,封装功能
-规则化思维:抽象过程为规则,计算机自动执行
-化繁为简:将大功能变小组合,分而治之
——————————————————————————————————————————————
557073083385
实例8:科赫雪花小包裹
描述
这是"实例"题,与课上讲解实例相同,请作答检验学习效果。
科赫曲线,也叫雪花曲线。绘制科赫曲线。
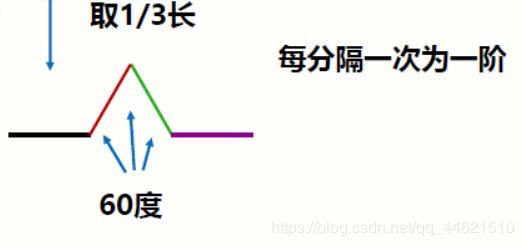
请补充编程模板中代码,完成功能:获得用户输入的整数N,作为阶,绘制N阶科赫曲线。
import turtle
def koch(size, n):
if n == 0:
turtle.fd(size)
else:
for angle in [0, 60, -120, 60]:
turtle.left(angle)
koch(size/3, n-1)
def main(level):
turtle.setup(600,600)
turtle.penup()
turtle.goto(-200, 100)
turtle.pendown()
turtle.pensize(2)
koch(400,level)
turtle.right(120)
koch(400,level)
turtle.right(120)
koch(400,level)
turtle.hideturtle()
try:
level = eval(input("请输入科赫曲线的阶: "))
main(level)
except:
print("输入错误")
(1) 基本思路:
-递归思想:函数 +分支
-递归链条:线段的组合
-递归基例:初始线段
(2) 分形几何是一种迭代的图,广泛存在于自然界中,请尝试选择一个新曲线绘制:
-康托尔集、谢宾斯基三角形门格海绵 …
-龙形曲线 、空间填充科赫…
-函数递归的深入应用 …
————————————————————————————————————————
任意累积
描述
请根据编程模板补充代码,计算任意个输入数字的乘积。
注意,仅需要在标注…的地方补充一行或多行代码。
def cmul(a, *b):
m = a
for i in b:
m *= i
return m
print(eval("cmul({})".format(input())))
该程序需要注意两个内容:
-
无限制数量函数定义的方法,其中b在函数cmul中表达除了a之外的所有输入参数;
-
以字符串形式调用函数的方法,"cmul()"与eval()的组合,提供了很多灵活性
——————————————————————————————————————————
斐波那契数列计算
描述
根据编程模板补充代码,计算斐波那契数列的值,具体功能如下:
-
获取用户输入整数N,其中,N为正整数
-
计算斐波那契数列的值
如果将斐波那契数列表示为fbi(N),对于整数N,值如下:
fbi(1)和fbi(2)的值是1,当N>2时,fbi(N) = fbi(N-1) + fbi(N-2)
请采用递归方式编写。
def fbi(n):
if n == 1 or n == 2:
return 1
else:
return fbi(n-1) + fbi(n-2)
n = eval(input())
print(fbi(n))
——————————————————————————————————————————
汉诺塔实践
描述
汉诺塔问题大家都清楚,这里不再赘述。
请补充编程模板中代码,完成如下功能:
有三个圆柱A、B、C,初始时A上有N个圆盘,N由用户输入给出,最终移动到圆柱C上。
每次移动步骤的表达方式示例如下:[STEP 10] A->C。其中,STEP是步骤序号,宽度为4个字符,右对齐。
请编写代码,获得输入N后,输出汉诺塔移动的步骤。
steps = 0
def hanoi(src, des, mid, n):
global steps
if n == 1:
steps += 1
print("[STEP{:>4}] {}->{}".format(steps, src, des))
else:
hanoi(src, mid, des, n-1)
steps += 1
print("[STEP{:>4}] {}->{}".format(steps, src, des))
hanoi(mid, des, src, n-1)
N = eval(input())
hanoi("A", "C", "B", N)
汉诺塔实例十分经典,学习每门语言都要写一遍。
这个例子要注意:全局变量的使用以及递归的用法。递归用法注意:函数定义+分支表示。
————————————————————————————————————————
欢迎关注我的公众号【panda一块砖】,更新更多编程相关文章与资源。