拟合与优化——利用Scipy包的optimize模块

chap 0 对数组的操作

0.1 python中的数组创建

无论matlab中还是在python中数组都是参与运算的重要甚至是唯一载体，在python的各种科学计算库中都是围绕ndarray对象展开的。尤其是在对数组中的各个元素进行运算的时候，数组像是一个数的集合，在定义函数时，是数和数之间的运算，实际传入参数时又可灵活地选择数组，当然原本返回的是一个数，现在也返回一个数组。故而，博主的python科学计算之旅也从数组开始。
但是，这只是小白的学习笔记，而不是本科全书式的字典，并不求全面，只求掌握内核与精髓（会用就行，暂且先做个APIboy）。

1 利用 numpy 的array()的函数

	np.array（list）

import numpy as np
a = np.array([1,2,3,4])
b = np.array([5,6,7,8])
# 二维数组类似于list的嵌套
c = np.array([1,2,3],
			 [2,3,4],
			 [4,5,6])

故而可以用各种方式（简单赋值，range（），列表推导式等等）来先生成一个list，在用array函数即可。

2 利用numpy库自身的创建数组的函数

2.1 利用arange()函数
np.arange(start,end,step) (左闭右开)

np.arange(0,1,0.1)
# 生成了 array([0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9])

2.2 利用 linspace()函数
np.linspace(start,end,numOfNumbers)

np.linsapce(0,5,6)
# array([0,1,2,3,4,5])

linspace（）与 arange（）的区别在于，前者关心个数，后者关心增量

2.3 利用logspace（）
np.logspace(start,end,numOfNumbers) 默认以 10 为底

np.logspace(0,2,5)
# array([1,3.16227766,10,31.622766,100])

0.2 对数组的四则运算

python是动态类型语言，事先无需声明变量的类型，为我们的创建与使用提供了方便（当然这也带来了负面影响）。这种灵活性的优势在数组的运算中可见一斑。

x = np.arange(1,100,2)
y = np.arange(0,99,2)
c = x+y
# 这种数组之间的运算，实际上是对数组对应的每一个元素进行运算，并且生成一个新的数组，本质上就是循环操作。

这种简洁性让正在学Java的博主感到很不适应。╮(╯▽╰)╭
诸如此类的 + - * / // 等等照搬过来即可

0.3 各种ufunc函数

ufunc 即 universal function的缩写，它是能对数组的每一个元素进行运算的的函数。
for example：

x = np.linspace(0,2*np.pi,10)
y = np.sin(x)

比如常用的sum函数

x=np.array([1,2,3])
np.sum(x)
# 6

凡此种种，不再列举。

chap 1 非线性方程组求解

求解非线性方程组，当然没有通用的解析方法，只能采取数值解法，本质上就是不断的猜测可能的一组解，带入方程对应的函数，使函数值逐渐逼近于0，所以这本质上也就是一个最优化的问题—— 使一个 向量值函数值 等于 零向量，即 $f$ ($x$) = $0$

1.1 基础版（不引入Jacobi矩阵 ）

我们的工具 fsolve（）函数
optimize.fsolve(func,x0)

func 即为误差函数（也就是方程组对应的那个向量值函数），x0 是初始设定的一组解,返回值即为方程组的解（一个数组）。
内部实现（博主的猜测）：传入一组初值，计算误差，根据误差，调整$x$，再次计算误差，直到误差小于阈值，然后终止循环，返回方程组的解$x$。

我们以下面的非线性方程组为例，
$$\{\begin{array}{c}5x_2+3=0\\ 4x_1^2-2sin(x_2{x}_3)=0\\ x_2{x}_3-1.5=0\end{array}$$
代码实现

from scipy import optimize
import numpy as np
def func(x):
    x1,x2,x3=x.tolist()
    return np.array([5*x2+3 , 4*x1*x1-2*np.sin(x2*x3) , x2*x3-1.5])
result = optimize.fsolve(func,[1,1,1])
wucha =func(result)
print("结果",result,"\n","误差",wucha)

结果 [-0.70622057 -0.6        -2.5       ] 
误差 [ 0.00000000e+00 -9.12603326e-14  5.32907052e-15]

1.2 优化版（引入Jacobi矩阵）

fsolve(）函数的一个可选参数为 fprime=jacobi (prime有导数的意思)
我们知道，向量值函数的导数是一个矩阵，此矩阵便是雅各比矩阵，记为J

而向量值函数的微分在某点处的微分即为
d $f$ ($x$) = Jd$x$。
然后，就没有然后了。。。因为博主并没有对fsolve的代码实现进行分析，但是我们可以相信，传入函数的导数，可以根据导函数的走向更方便的逼近正确解。

def jac(x):
    x1,x2,x3=x.tolist()
    return np.mat([[0,5,0],
           [8*x1,-2*x3*cos(x2*x3),-2*x2*cos(x2*x3)],
           [0,x3,x2]
        ])
    
better_result = optimize.fsolve(func,[1,1,1],fprime=jac) 
print("结果",better_result,"\n","误差",func(better_result))

结果 [-0.70622057 -0.6        -2.5       ] 
误差 [ 0.00000000e+00 -9.12603326e-14  5.32907052e-15]

(╮(╯▽╰)╭，发现结果并没有什么差异)
但，fprime参数的传递可以更快的进行求解，尤其是在方程组的未知量很多的时候（50个以上，嗯，确实够多的……），求解速度可以提高好几倍。

chap 2 最小二乘拟合¹

所谓拟合，就是有一组实验数据（离散的），我们猜测它们应该满足某种函数关系，比如线性关系，对数关系等，然后我们需要确定这个函数的一些参数（比如线性函数的斜率k和纵截距b），不妨用 $p$来表示这样的一组参数（$p$就实现为数组）。但我们用函数来刻画这种关系，当然希望误差最小，而这误差总要有一个标准。
标准可以是，找一个 p使得下式最小：
$$S(p)=\sum _{i=1}^m(y_i-f(x_i,p){)}^2$$
$x_i,y_i$即为已知的一组实验数据，所以，S（p）即为关于p的一个函数（实际上是个多元数量值函数）。
基于这种标准的拟合就是 最小二乘拟合。

2.1 以线性函数 y=kx+b 为例

现在，我们发现拟合问题又转化为一个 求一组解，使函数值最小的问题了，

 我们的工具 leastsq（）函数，而它可以做到 求
 sum((ydata - f(xdata, params))**2) 的minimum	

于是optimize模块又可大显神通。

我们的工具
将要拟合的函数(p为待定值)：
def func(x,p):
	return 
x,y可传递为数组，则wucha()也返回一个数组
def wucha(p，x,y):
	return y-func(x,p)
X，Y为实验数据 ; p0初始化
result = optimize.leastsq(wucha,p0,args=(X,Y))

下面以线性函数为例：

import numpy as np
from scipy import  optimize
"""
实验给定的一组数据，我们猜测其为线性关系
"""
X = np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
Y = np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])

def wucha(p,x,y):
    k,b = p  # python的及其简洁的语法，一度让我很不适应
    return y-(k*x+b)
result = optimize.leastsq(wucha,[1,0],args=(X,Y))
k,b = result[0];
# result 实际上为 (array([0.61349535, 1.79409254]), 1)
print('k=',k,'b=',b)

	k= 0.6134953491930442 b 1.794092543259387

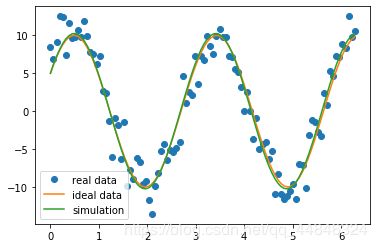
可视化分析：发现拟合情况非常好，绿线与黄线几乎重合

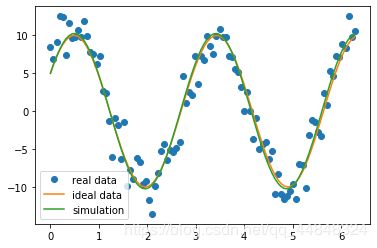
ps： [1,0],X，Y分别作为实参赋值给wucha(p,x,y)的形参p,x,y,wuch()会返回一个误差数组，leastsq函数对此求和，然后，根据返回值，调整p，循环往复，直到值最小，此时的p便是我们所求（还是和上面的一样，对optimize的实现不清楚，只能瞎说说了）

2.2 以三角函数 y=Asin(2$\pi$k+$\theta$)为例

下面我们以带有噪声的一组数据为例：
一个波，我们猜测它为一个正弦波参杂了噪声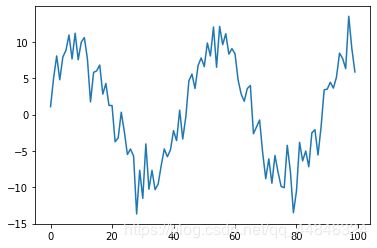

# -*- coding: utf-8 -*-
import numpy as np
import scipy as sp
import matplotlib.pylab as pl
def target(x,p):
    A,k,theta = p
    return A*np.sin(2*np.pi*k*x+theta)
def wucha(p,ydata,xdata):
    return ydata - target(xdata,p)
"""
人工设置一组实验值，并且加上干扰值（否则拟合就没有意义了）
"""
xdata = np.linspace(0,2*np.pi,100)
p_real=[10,0.34,np.pi/6]
ydata_real= target(xdata,p_real)
np.random.seed(0)#设置一个种子值
ydata= ydata_real+ 2*np.random.randn(len(xdata))#真实数据

p0=[7,0.4,0]
result = sp.optimize.leastsq(wucha,p0,args=(ydata,xdata))

print("真实参数",p_real)
print("拟合参数",result[0])
#画个图，可视化一下
pl.plot(xdata,ydata,"o",label="real data")
pl.plot(xdata,ydata_real,label="ideal data")
pl.plot(xdata,target(xdata,result[0]),label="simulation")
pl.legend(loc="best")

真实参数 [10, 0.34, 0.5235987755982988]
拟合参数 [ 9.44553351  0.41676239 -0.04808953]

可视化分析：

chap 3 求函数局域最优解

在这里，会简单介绍一下利用optimize的minimize方法来求一个多元函数的操作方法，如前面的思想一样，只介绍怎么操作，不关心内部实现以及数学原理。

我们的工具：optimize.minimize

optimize.minimize(func,init_point,method,jac,hess)

以Rosenbrock函数为例：
$$f(x,y)=(1-x{)}^2+100(y-x^2{)}^2$$
此函数很难搜索到最小值点，常用来检验各种算法（当然我们其实一眼就能看到其最小值在（1，1）处取得）
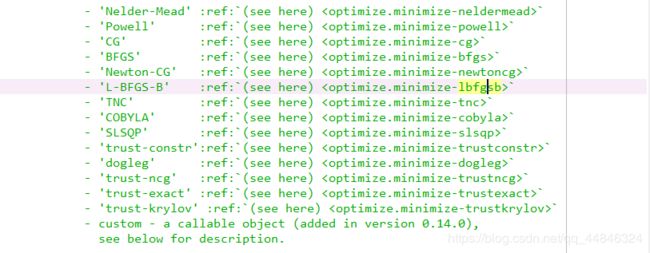
我们采用一种比较先进的算法 L-BFGS-B ²,当然还有其他多种，下图是博主截取的API文档

import numpy as np
from scipy import optimize
#目标导数
def target_function(p):
    x,y =p.tolist()
    z = (1-x)**2+100*(y-x**2)**2
    return z
#一阶导数
def fjac(p):
    x,y =p.tolist()
    dx = -2+2*x-400*x*(y-x**2)
    dy = 200*y-200*x**2
    return np.array([dx,dy])
#二阶导数
def fhess(p):
    x,y =p.tolist()
    dxdx = 2*(600*x**2-200*y+1)
    dxdy = -400*x
    dydx = -400*x
    dydy = 200
    return np.array([dxdx,dxdy],[dydx,dydy])
# 初始猜测点
init_point = [-1,-1]
method = "L-BFGS-B"
result = optimize.minimize(target_function,init_point,
                    method=method,jac=fjac,hess=fhess)
print("极小值",result["fun"],"\n极小值点",result["x"])

极小值 6.521501346206669e-15 
极小值点 [0.99999994 0.99999987]

ps：这里我们要求的就是一个极值点，所以在函数，一阶导，二阶导的参数必须是一个数组参数，否则会报错（target_function() missing 1 required positional argument）

chap 4求全域最优解

我们的工具：optimize.basinhopping

optimize.basinhopping(func,init_point,niter,minimizer_kwargs) 
niter为迭代次数

下面简单的介绍一下optimize的basinhopping方法求函数的最小值，这里仍需用到搜索局部最小值的算法。
这里以一个的二元函数为例，

from scipy import optimize
import numpy as np
def target(p):
    x,y=p
    return (x-1)*(x-2)*(x-3)*(x-4)*(x-5)*(x-6)*np.sin(y)


result = optimize.basinhopping(target,[1,1],niter=10,
                               minimizer_kwargs={"method":"L-BFGS-B",
                                                 })
print("最值点",result["x"],"\n最小值",result["fun"])

最值点 [1.33655347 1.57079634] 
最小值 -16.900894327379042

附上两篇很好的文章

---

1. 关于最小二乘法 ↩︎

2. L-BFGS-B算法 ↩︎