14案例实战：泰坦尼克获救预测（线性回归、逻辑回归、随机森林、Kfold交叉验证、Bagging类型集成算法）

唐宇迪《python数据分析与机器学习实战》学习笔记
14案例实战：泰坦尼克获救预测

目的：将之前学过的机器学习算法应用在实际场景中，这里使用的是泰坦尼克号获救数据

一、数据观察与预处理

数据如下：1列为编号，2列为是否存活（标签），然后分别为船舱等级、姓名、性别、年龄、船上多少个亲人(SibSp)、船上你的老人＋孩子多少个(Parch)、船票编号(Ticket)、船票价格(Fare)、船舱位（Cabin缺失多）、上船码头(Embarked)。

1.1 数据导入

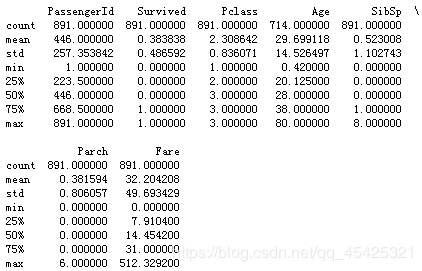
数据导入，并统计一下每个特征：发现age有缺失值。（备注：现在传入的数据，为训练数据集）

import pandas
titanic = pandas.read_csv('titanic_train.csv')
print(titanic.describe())

1.2 缺失值填充

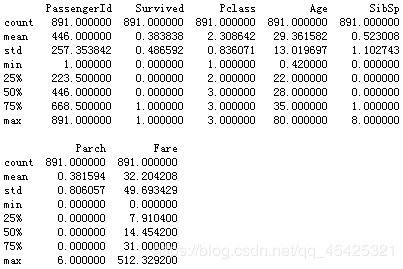
这里利用平均年龄对缺失值进行填充：

titanic['Age'] = titanic['Age'].fillna(titanic['Age'].median())
print(titanic.describe())

1.3 字符量映射为数值量

print (titanic['Sex'].unique()) #看一下这列有几种可能性，这里两种
titanic.loc[titanic['Sex']== 'male','Sex']=0     #男士映射为0
titanic.loc[titanic['Sex']=='female','Sex']=1   #女士映射为1

[‘male’ ‘female’]

print (titanic['Embarked'].unique())
titanic['Embarked'] = titanic['Embarked'].fillna('S')  #众数填充
titanic.loc[titanic['Embarked']== 'S','Embarked']=0
titanic.loc[titanic['Embarked']=='C','Embarked']=1
titanic.loc[titanic['Embarked']=='Q','Embarked']=2

[‘S’ ‘C’ ‘Q’ nan]

二、模型训练及预测

下面我们分别用线性模型、逻辑回归、随机森林这三种机器学习算法模型来分析这个案例，就是分析生存率

2.1 .线性回归模型

首次使用线性回归算法进行分类，数据交叉验证分割为3份，每份轮流作验证集，其他作训练集

from sklearn.linear_model import LinearRegression  
#导入线性回归
from sklearn.model_selection import KFold
#交叉验证，把训练数据集分成三份，1份验证2份训练模型，最后取平均值

predictors = ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked']
#要给我的分类器哪些特征

alg = LinearRegression()
# kf = KFold(titanic.shape[0], n_folds=3, random_state=1) 写法错误已被弃用 
kf = KFold(n_splits=3,shuffle=False, random_state=1)#shuffle每次划分时是否洗牌 random_state随机种子数

predictions = []   #装预测结果
#for train,test in kf 写法错误已被弃用 
for train, test in  kf.split(titanic): #3份轮流当测试和验证
    #得到训练集的特征与标签
    train_predictors = (titanic[predictors].iloc[train,:])#特征，用iloc选出作为训练集标签的行
    train_target = titanic['Survived'].iloc[train]  #标签
    alg.fit(train_predictors,train_target) #建模
    #传入验证集的特征值，进行预测
    test_predictions = alg.predict(titanic[predictors].iloc[test,:])
    #每次加入结果（一大堆概率值），共三次，组成拥有3个数组的数组数据。
    predictions.append(test_predictions)

接着算出线性回归准确率，将刚才得到的预测值中的3个数组合并，然后以0.5为分界值将结果映射，计算准确率

import numpy as np
#这些预测在三个独立的numpy数组中。把它们连接成一个。
predictions = np.concatenate(predictions,axis=0) 

# 映射成分类结果,计算准确率
predictions[predictions > .5] = 1  
predictions[predictions <= .5] = 0
#用预测对的/总的
accuracy = sum(predictions==titanic['Survived'])/len(predictions)
print(accuracy)

0.7037037037037037
二分类问题，瞎猜都50%，因此这个准确率并不高

2.2 逻辑回归模型

from sklearn.model_selection import cross_val_score #k 折交叉验证，切三份每份轮流当验证
from sklearn.linear_model import LogisticRegression #逻辑回归模型传入
 
alg = LogisticRegression(random_state=1)
scores = cross_val_score(alg, titanic[predictors], titanic["Survived"], cv=3) #cv为可迭代的次数

print(scores.mean())

0.7081930415263749
结果略微变好
为了便于理解 上面cross_val_score的K折法这里传入下图10折参考：

2.3 随机森林

以上都是用交叉分类后的训练数据集进行分类，实际中应该对测试数据集进行分类。
接下来传入测试数据集，重复刚才在训练集上的填充、映射操作。

titanic_test = pandas.read_csv("test.csv")
titanic_test["Age"] = titanic_test["Age"].fillna(titanic["Age"].median())
titanic_test["Fare"] = titanic_test["Fare"].fillna(titanic_test["Fare"].median())
titanic_test.loc[titanic_test["Sex"] == "male", "Sex"] = 0
titanic_test.loc[titanic_test["Sex"] == "female", "Sex"] = 1
titanic_test["Embarked"] = titanic_test["Embarked"].fillna("S")
 
titanic_test.loc[titanic_test["Embarked"] == "S", "Embarked"] = 0
titanic_test.loc[titanic_test["Embarked"] == "C", "Embarked"] = 1
titanic_test.loc[titanic_test["Embarked"] == "Q", "Embarked"] = 2

通过上面线性回归和逻辑回归发现效果似乎都不太理想，因此尝试一下随机森林，随机森林一般比前两者效果都要好，这里需要着重注意一下随机森林的参数变化

# 导入需要用的库
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier

#需要使用的特征
predictors = ["Pclass", "Sex", "Age", "SibSp", "Parch", "Fare", "Embarked"]

#构造树模型
alg = RandomForestClassifier(random_state=1,
                             n_estimators=10, #构造10棵树
                             min_samples_split=2,#最小切分点，2个时不切了
                             min_samples_leaf=1) #叶子节点最少个数
#一般不希望树的高度太高，可能过拟合，切得太碎可能因为噪音点而切

#交叉验证,3折
kf = KFold(n_splits=3, shuffle=False, random_state=1)
#得到分值（准确率），每次交叉验证得到分值，这里得到3个
scores = cross_val_score(alg, titanic[predictors], titanic["Survived"], cv=kf)

print(scores.mean())#取三个平均

0.7856341189674523
这里结果有所提升，但是还是不理想，因此通过参数调节对模型进行优化

随机森林参数调节
最需要调整建立多少棵树，因此这里试一下建立100棵树 （后面两个参数也可以调节）

alg = RandomForestClassifier(random_state=1,
                             n_estimators=100,
                             min_samples_split=4,
                             min_samples_leaf=2)
kf = KFold(n_splits=3, shuffle=False, random_state=1)
scores = cross_val_score(alg, titanic[predictors], titanic["Survived"], cv=kf)

print(scores.mean())

0.8148148148148148
结果又有所提升，假设此时模型优化得差不多了，前面三种方法得到的结果最高也不理想，达到了准确率瓶颈，想要继续优化，此时就回归数据本身。影响分类器最多的还是输入数据本身。刚才输入特征有限，接下来构造新特征，比如：家庭成员＋名字长度。

三、特征创造及重要性衡量（feature_selection）

本质是：通过加入噪音值前后的错误率的差值来判断特征值的重要程度。

3.1 特征创造

titanic["FamilySize"] = titanic["SibSp"] + titanic["Parch"] #船上多少个亲人+船上你的老人＋孩子多少个
 
titanic["NameLength"] = titanic["Name"].apply(lambda x: len(x)) #用名字长度创造一列

这里观察名字列发现还带有一些称谓，比如博士、小姐等等，代表了一定的社会身份，因此这里也提取出来。

import re #正则表达式

# 构造一个函数去获取
def get_title(name):
    # 使用正则表达式搜索
    #称谓如Mr.通常由大写字母和小写字母组成，并以句号结尾，把格式写成正则表达式并搜索
    title_search = re.search(' ([A-Za-z]+)\.', name)  #，A-Z所有的大写字母，a-z所有的小写字母，+表示出现≥1次，\.匹配句号
    # 如果称谓存在就提取，然后返回值
    if title_search:
        return title_search.group(1)
    return ""
     
# 这里获取所有的称谓，并打印每一个称谓出现数量
titles = titanic["Name"].apply(get_title)
print(pandas.value_counts(titles))
 
# 将称谓字符串映射为整数。有些少见的称谓就干脆和其他一起映射
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Dr": 5, "Rev": 6, "Major": 7, "Col": 7, "Mlle": 8, "Mme": 8, "Don": 9, "Lady": 10, "Countess": 10, "Jonkheer": 10, "Sir": 9, "Capt": 7, "Ms": 2}
for k, v in title_mapping.items():
    titles[titles == k] = v
 
# 看一下转换结果
print(pandas.value_counts(titles))
 
# 添加一列装入数据
titanic["Title"] = titles

Mr 517
Miss 182
Mrs 125
Master 40
Dr 7
Rev 6
Col 2
Mlle 2
Major 2
Lady 1
Sir 1
Jonkheer 1
Ms 1
Capt 1
Mme 1
Don 1
Countess 1
Name: Name, dtype: int64
1 517
2 183
3 125
4 40
5 7
6 6
7 5
10 3
8 3
9 2
Name: Name, dtype: int64

3.2 特征重要性判断

现在弄出了一大堆特征，这里选择出最有价值的特征，利用前面提到的随机森林特征重要性判断。
例如：12345特征建立随机森林模型，得到一个错误率erro1；判断某个特征重要性，就用噪音值替换该特征，然后得到一个错误率erro2，比较两个错误率，看重要性。

import numpy as np
from sklearn.feature_selection import SelectKBest, f_classif
import matplotlib.pyplot as plt

predictors = ["Pclass", "Sex", "Age", "SibSp", "Parch", "Fare", "Embarked",
              "FamilySize","Title", "NameLength"]
 
# 建立特征选择模型，传入特征及标签
selector = SelectKBest(f_classif, k=5)
selector.fit(titanic[predictors], titanic["Survived"])
 
# 获取每个特性的原始p值，并通过log函数转换为分数
scores = -np.log10(selector.pvalues_)
 
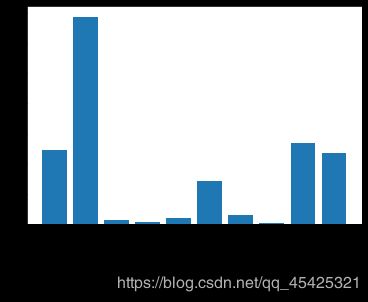
# 可视化展示，“Pclass”、“Sex”、“Title”和“Fare”最佳
plt.bar(range(len(predictors)), scores)
plt.xticks(range(len(predictors)), predictors, rotation='vertical')
plt.show()
 
# 只选择4个最好的特征
predictors = ["Pclass", "Sex", "Fare", "Title"]

#建立随机森林
alg = RandomForestClassifier(random_state=1, n_estimators=50,min_samples_split=8,min_samples_leaf=4)
kf = KFold(n_splits=3, shuffle=False, random_state=1)
scores = cross_val_score(alg, titanic[predictors], titanic["Survived"], cv=kf)
print(scores.mean())

0.819304152637486
从图中分析出，4个最重要特征为船舱等级、性别、船票、称谓，取出来用，剔除不重要项。
上面都是单个分类器，这里引进集成算法

四、集成算法

4.1 梯度增强+逻辑回归

from sklearn.ensemble import GradientBoostingClassifier
import numpy as np
 
#这里集成两个算法，在逻辑回归中使用了更线性的预测器，以及梯度增强分类器。
algorithms = [
    [GradientBoostingClassifier(random_state=1, n_estimators=25, max_depth=3), ["Pclass", "Sex", "Age", "Fare", "Embarked", "FamilySize", "Title",]],
    [LogisticRegression(random_state=1,solver='liblinear'), ["Pclass", "Sex", "Fare", "FamilySize", "Title", "Age", "Embarked"]]  
]     #solver优化算法选择参数，liblinear指用坐标轴下降法来迭代优化损失函数
 
# 交叉验证
kf = KFold(n_splits=3,shuffle=False, random_state=1)
 
predictions = [] #装最终预测分类值
for train, test in kf.split(titanic):
    train_target = titanic["Survived"].iloc[train]#训练集标签
    full_test_predictions = []#装两个分类器预测值
    # 对每个折叠中的每个算法进行预测
    for alg, predictors in algorithms:
        # 训练集训练模型
        alg.fit(titanic[predictors].iloc[train,:], train_target)
        # astype(float)是将数据aframe转换为所有浮点数并避免sklearn错误所必需的。
        test_predictions = alg.predict_proba(titanic[predictors].iloc[test,:].astype(float))[:,1]
        full_test_predictions.append(test_predictions)
    #  两个分类器取平均结果
    test_predictions = (full_test_predictions[0] + full_test_predictions[1]) / 2 
    # 映射结果值
    test_predictions[test_predictions <= .5] = 0
    test_predictions[test_predictions > .5] = 1
    predictions.append(test_predictions)
 
# 将所有的预测放在一个数组中
predictions = np.concatenate(predictions, axis=0)
 
# 精度计算
accuracy = sum(predictions == titanic["Survived"]) / len(predictions)
print(accuracy)

0.8215488215488216

4.2 使用测试数据预测

代入测试数据集来进行预测(不过在测试数据集里面没有"Survived"这一列，就只能进行预测了)
数据预处理

titles = titanic_test["Name"].apply(get_title)
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Dr": 5, "Rev": 6, "Major": 7, "Col": 7, "Mlle": 8, "Mme": 8, "Don": 9, "Lady": 10, "Countess": 10, "Jonkheer": 10, "Sir": 9, "Capt": 7, "Ms": 2, "Dona": 10}
for k,v in title_mapping.items():
    titles[titles == k] = v
titanic_test["Title"] = titles
# 检查每个唯一标题的计数
print(pandas.value_counts(titanic_test["Title"]))

# 现在，我们添加family size列
titanic_test["FamilySize"] = titanic_test["SibSp"] + titanic_test["Parch"]

1 240
2 79
3 72
4 21
7 2
6 2
10 1
5 1
Name: Title, dtype: int64

predictors = ["Pclass", "Sex", "Age", "Fare", "Embarked", "FamilySize", "Title"]

algorithms = [ [GradientBoostingClassifier(random_state=1, n_estimators=25, max_depth=3), predictors],
    [LogisticRegression(random_state=1), ["Pclass", "Sex", "Fare", "FamilySize", "Title", "Age", "Embarked"]]]

full_predictions = []
for alg, predictors in algorithms:
    # 使用完整的训练数据拟合算法
    alg.fit(titanic[predictors], titanic["Survived"])
    # 使用测试数据集进行预测。我们必须将所有列转换为浮点数以避免错误
    predictions = alg.predict_proba(titanic_test[predictors].astype(float))[:,1]
    predictions[predictions <= .5] = 0
    predictions[predictions > .5] = 1
    full_predictions.append(predictions)

# 梯度增强分类器能够产生更好的预测，因此我们对其进行了更高的加权
#predictions = (full_predictions[0] * 3 + full_predictions[1]) / 4
predictions

array([0., 0., 0., 0., 1., 0., 1., 0., 1., 0., 0., 0., 1., 0., 1., 1., 0.,
0., 1., 1., 0., 0., 1., 1., 1., 0., 1., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 0., 0., 1., 0., 0.,
0., 1., 1., 0., 0., 0., 0., 0., 1., 0., 0., 0., 1., 1., 1., 1., 0.,
0., 1., 1., 0., 1., 0., 1., 1., 0., 1., 0., 1., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 1., 1., 0., 1., 0., 1., 0., 1., 0., 1., 0., 1., 0.,
0., 0., 1., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 1., 0.,
1., 1., 0., 1., 0., 0., 1., 0., 1., 0., 0., 0., 1., 0., 0., 0., 0.,
0., 0., 1., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.,
0., 0., 0., 1., 1., 0., 1., 1., 0., 1., 0., 0., 1., 0., 0., 1., 1.,
0., 0., 0., 0., 0., 1., 1., 0., 1., 1., 0., 0., 1., 0., 1., 0., 1.,
0., 0., 0., 0., 0., 0., 0., 1., 0., 1., 1., 0., 1., 1., 0., 1., 1.,
0., 0., 1., 0., 1., 0., 0., 0., 0., 1., 0., 0., 1., 0., 1., 0., 1.,
0., 1., 0., 1., 1., 0., 1., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.,
1., 1., 1., 1., 0., 0., 0., 0., 1., 0., 1., 1., 1., 0., 1., 0., 0.,
0., 0., 0., 1., 0., 0., 0., 1., 1., 0., 0., 0., 0., 1., 0., 0., 0.,
1., 1., 0., 1., 0., 0., 0., 0., 1., 0., 1., 1., 1., 0., 0., 0., 0.,
0., 0., 1., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.,
0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0.,
0., 1., 0., 1., 0., 0., 0., 1., 0., 0., 1., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 1., 0., 1., 0., 1., 0., 1., 1., 0., 0., 0., 1., 0., 1.,
0., 0., 1., 0., 1., 1., 0., 1., 0., 0., 1., 1., 0., 0., 1., 0., 0.,
1., 1., 1., 0., 0., 0., 0., 0., 1., 1., 0., 1., 0., 0., 0., 0., 1.,
1., 0., 0., 0., 1., 0., 1., 0., 0., 1., 0., 1., 1., 0., 0., 0., 0.,
1., 1., 1., 1., 1., 0., 1., 0., 0., 0.])