用人工神经网络来逼近股票价格
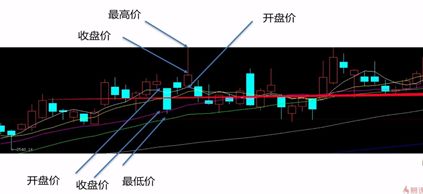
(上图是某个模板的股票交易图,图中的每个矩形的颜色代表了一天的执行价格,红色矩形表示当前的股票是上涨的,蓝色的矩形表示当前的股票是下降的,股票是每天上午9点开盘,下午3点关盘,红色代表了当天下午3点关盘的价格大于上午9点开盘的价格,蓝色反是如此。)
import numpy as np
import matplotlib.pyplot as plt
data = np.linspace(1,15,15) #日期,在0-15之间等分,分成15份
endprice = np.array([2511.90,2538.26,2510.68,2591.66,2732.98,2701.69,2701.29,2678.67,2726.50,
2681.50,2739.17,2715.07,2823.58,2864.90,2919.08])#收盘价格
beginprice = np.array([2438.71,2500.88,2534.95,2512.52,2594.04,2743.26,2697.47,2695.24,2678.23,
2722.13,2674.93,2744.13,2717.46,2832.73,2877.40])#开盘价格
print(data) #打印检查下日期是否正确显示
plt.figure()
for i in range(0,15):
#柱状图,需要x,y坐标,需要每一天的时间和开关盘价格
dataOne = np.zeros([2]) #用来记录开盘和关盘的日期,日期一样
dataOne[0] = i #开盘的日期
dataOne[1] = i #关盘的日期
priceOne = np.zeros([2]) #用来记录开盘价格和关盘价格
priceOne[0] = beginprice[i]
priceOne[1] = endprice[i]
#接下来开始绘制柱状图
#需要判断当天的股票是上涨还是下降
if endprice[i] > beginprice[i]:
plt.plot(dataOne,priceOne,'r',lw=8)
else:
plt.plot(dataOne,priceOne,'g',lw=8)
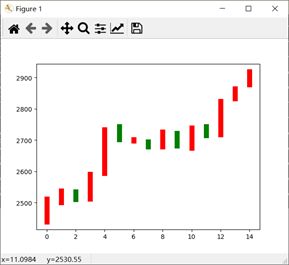
plt.show()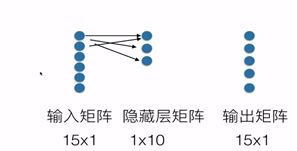
输入:天数 A * w1 + b1 = B——第一层和第二层的关系
输出:每天股价 B * w2 + b2 = C——第二层和第三层的关系
(其中,w1和w2是权重矩阵,b1和b2是偏置矩阵,A:输入层;B:隐藏层;C:输出层)
w1:1×10的矩阵 w2:10×1的矩阵
b1: 1×10的矩阵 b2:15×1的矩阵
A(15×1) × w1(1×10)+b1(15×10) = B(15×10) (矩阵之间的乘法)
B(15×10) × w2(10×1)+b2(15×1)= C(15×1)
工作原理:
第1次循环A=1天:(假设w1=0.1,w2=0.1,b1=0.2,b2=0.3)可以算出来C
假设算出来2400,目标值是2511,误差为111点
第2次循环:使用梯度下降法,目的使误差111减少,(假设w1=0.11,w2=0.09,b1=0.22,b2=0.34)可以算出来C=2450,误差为61
终止条件:误差为2%为止
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
data = np.linspace(1,15,15) #日期,在0-15之间等分,分成15份
endPrice = np.array([2511.90,2538.26,2510.68,2591.66,2732.98,2701.69,2701.29,2678.67,2726.50,
2681.50,2739.17,2715.07,2823.58,2864.90,2919.08])#收盘价格
beginPrice = np.array([2438.71,2500.88,2534.95,2512.52,2594.04,2743.26,2697.47,2695.24,2678.23,
2722.13,2674.93,2744.13,2717.46,2832.73,2877.40])#开盘价格
print(data) #打印检查下日期是否正确显示
plt.figure()
for i in range(0,15):
#柱状图,需要x,y坐标,需要每一天的时间和开关盘价格
dataOne = np.zeros([2]) #用来记录开盘和关盘的日期,日期一样
dataOne[0] = i #开盘的日期
dataOne[1] = i #关盘的日期
priceOne = np.zeros([2]) #用来记录开盘价格和关盘价格
priceOne[0] = beginPrice[i]
priceOne[1] = endPrice[i]
#接下来开始绘制柱状图
#需要判断当天的股票是上涨还是下降
if endPrice[i] > beginPrice[i]:
plt.plot(dataOne,priceOne,'r',lw=8)
else:
plt.plot(dataOne,priceOne,'g',lw=8)
#A:输入层
dataNormal = np.zeros([15,1]) #初始化15*1的矩阵
priceNormal = np.zeros([15,1])
for i in range(0,15):
dataNormal[i,0] = i/14.0 #日期最大是14,这里除以14.0,转为浮点数
priceNormal[i,0] = endPrice[i]/3000.0; #让最大值不超过3000
#数据的装载方式
x = tf.placeholder(tf.float32,[None,1]) #表示N行1列
y = tf.placeholder(tf.float32,[None,1])
#B:隐藏层
w1 = tf.Variable(tf.random_uniform([1,10],0,1)) #因为w1等要修改,所以定义为变量,随机数
#random_uniform表示产生一个1*10的随机矩阵,范围是0到1
b1 = tf.Variable(tf.zeros([1,10])) #这里不懂为什么不是15*10??????
wb1 = tf.matmul(x,w1)+b1 #matmulb表示矩阵的乘法 即A*w1+b1 = B,得到隐藏层
#激励函数:作用是将上面的结果进行了映射,变成了另外的值
layer1 = tf.nn.relu(wb1) #激励函数
#C:输出层
w2 = tf.Variable(tf.random_uniform([10,1],0,1))
b2 = tf.Variable(tf.zeros([15,1]))
wb2 = tf.matmul(layer1,w2)+b2 #matmulb表示矩阵的乘法 即B*w2+b2 = C,得到输出层
layer2 = tf.nn.relu(wb2) #激励函数
loss = tf.reduce_mean(tf.square(y-layer2)) #真实值y-计算值layer2
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) #梯度下降的步值
#利用梯度下降法最小化误差值loss
#开始训练数据
with tf.Session() as sess:
sess.run(tf.global_variables_initializer()) #当前变量初始化
#设置终止条件
for i in range(0,10000): #设置训练次数为10000次
sess.run(train_step,feed_dict={x:dataNormal,y:priceNormal})
"""运作流程:train_step调用梯度下降法GradientDescentOptimizer不断
减小loss,而loss又会把得到的计算值进行作差操作(y-layer2),
而计算值又来源于隐藏层即*w2+b2,而隐藏层又来源于x的值即*w1+b1,
所以归根到底,输入全是来自于x和y,所以我们输入x和y的值。
"""
pred = sess.run(layer2,feed_dict={x:dataNormal}) #给个预测结果
"""上句代码的作用:经过上句代码之后,训练出一组非常优化的w1、w2、
b1、b2,如何检测?通过给出一个新的输入层,加上w1、w2、b1、b2,
得出新的预测值,放入layer2中,通过绘制出来来检测是否准确。"""
predPrice = np.zeros([15,1])
for i in range(0,15):
predPrice[i,0] = (pred*3000)[i,0]
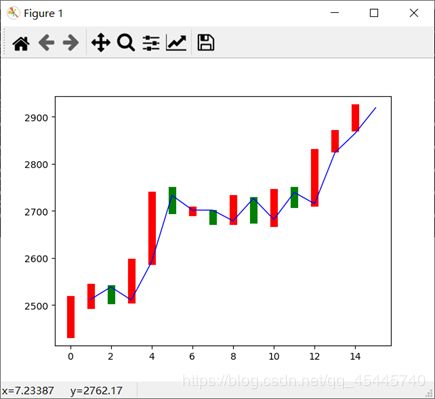
plt.plot(data,predPrice,'b',lw=1)
plt.show()