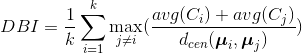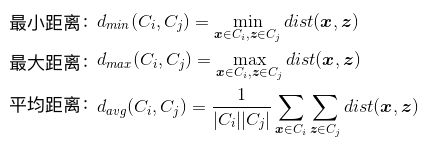聚类
目录
1、聚类任务
2、性能度量
外部指标
内部指标
3、原型聚类
k均值聚类
学习向量化
4、密度聚类
5、层次聚类
1、聚类任务
目标:通过对无标记训练样本的学习来揭示数据的内在性质和规律,为进一步数据分析提供基础。
聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个“簇”,每个簇可能对应于一些潜在的概念(类别),这些概念对聚类算法而言事先是未知的。
形式化来说,设样本集
包含m个无标记样本,每个样本
是一个n维特征向量。
则聚类算法将样本集D划分为k个不相交的簇
,其中
且
。
相应的,用
表示样本
的“簇标记”,即
,于是聚类的结果可用包含m个元素的簇标记向量
表示。
2、性能度量
性能度量又称聚类“有效性指标”,(1)需要某种性能度量来评估聚类结果的好坏;(2)可直接将其作为聚类过程的优化目标。
我们期望聚类的结果“簇内相似度”高且“簇间相似度”低。
外部指标
对数据集![]() ,假定通过聚类给出的簇划分为
,假定通过聚类给出的簇划分为![]() ,参考模型给出的簇划分
,参考模型给出的簇划分![]() ,相应的,令
,相应的,令![]() 与
与![]() 分别表示
分别表示![]() 与
与![]() 对应的簇标记向量,将样本两两配对考虑(共有m(m-1)/2个pair对,即
对应的簇标记向量,将样本两两配对考虑(共有m(m-1)/2个pair对,即![]() ),定义
),定义
其中,我们发现,相对于参考模型,a是必定正确的(集合SS包含pair对在两个模型均在相同簇),b(集合SD包含pair对在![]() 中属于相同簇,在
中属于相同簇,在![]() 中属于不同簇)和c(集合DS包含pair对在
中属于不同簇)和c(集合DS包含pair对在![]() 中属于不同簇,在
中属于不同簇,在![]() 中属于相同簇)是必定错误的,d(集合DD包含pair对在两个模型均在不同簇)是待定的(无法判断对错)。
中属于相同簇)是必定错误的,d(集合DD包含pair对在两个模型均在不同簇)是待定的(无法判断对错)。
Jaccard系数(JC):
![]()
FM指数(FMI):
![]()
Rand指数(RI):
![]()
显然,上述性能度量(JC、FMI和RI)的结果值均在[0,1]区间,值越大越好。
内部指标
考虑聚类结果的簇划分![]() ,定义
,定义
其中,![]() 用于计算两个样本之间的距离;
用于计算两个样本之间的距离;![]() 代表簇C的中心点
代表簇C的中心点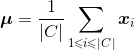 。显然,avg(C)对应于簇C内样本间的平均距离,diam(C)对应于簇C内样本间的最远距离,
。显然,avg(C)对应于簇C内样本间的平均距离,diam(C)对应于簇C内样本间的最远距离,![]() 对应于簇
对应于簇![]() 与簇
与簇![]() 最近的样本间的距离,
最近的样本间的距离,![]() 对应于簇
对应于簇![]() 与簇
与簇![]() 中心点的距离。
中心点的距离。
DB指数(DBI):
Dunn指数(DI)
显然,DBI的值越小越好,而DI则相反,值越大越好。
3、原型聚类
原型聚类也称作“基于原型的聚类”,此类算法假设聚类结构可以通过一组原型刻画,在现实任务中极为常见。(“原型”是指样本空间中具有代表性的点)通常情况下,算法先对原型进行初始化,然后对原型进行迭代更新求解。采用不同的原型表示、不同的求解方式,将产生不同的算法,下面介绍几种著名的原型聚类算法。
k均值聚类
给定样本集![]() ,“k均值”算法针对聚类所得簇划分
,“k均值”算法针对聚类所得簇划分![]() 最小化平方误差
最小化平方误差
其中![]() 是簇
是簇![]() 的均值向量。式(1)在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,E值越小则簇内样本相似度越高。要想直接找到式(1)的最优解不太容易,因为需要考察样本集D所有可能的簇划分,这是一个NP难问题。因此k均值法采用了贪心策略,通过迭代优化来近似求解上式。
的均值向量。式(1)在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,E值越小则簇内样本相似度越高。要想直接找到式(1)的最优解不太容易,因为需要考察样本集D所有可能的簇划分,这是一个NP难问题。因此k均值法采用了贪心策略,通过迭代优化来近似求解上式。
过程:
- 初始化k个均值向量
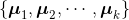 ,即k个簇的中心
,即k个簇的中心 - 循环迭代(直到满足最大的运算轮数或调整幅度小于阈值)。
- 将m个样本分配到距离最近的簇(到簇中心的距离最小)
- 依据新划分的簇计算新的均值向量
k均值算法的缺点:
- 需要事先确定簇的个数即k值(是一个超参数)
- 对噪声和离群点敏感
- 结果不一定是全局最优,只能保证局部最优
如何初始化簇中心:
- 随机初始化
- 选择彼此距离尽可能远的K个点。首先随机选择一个点作为第一个初始类簇中心点,然后选择距离该点最远的那个点作为第二个初始簇中心点,然后再选择距离前两个点的最近距离最大的点作为第三个初始簇中心点,一次类推,直到选出k个初始中心点。
- 先对数据用层次聚类算法或Canopy算法进行聚类,得到k个簇之后,从每个簇中选择一个点,该点可以是该簇的中心点,或者是距离类簇中心最近的那个点。
学习向量化
“学习向量化”(LVQ):假设样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。
给定样本集![]() ,每个样本
,每个样本![]() 是一个n维特征向量,
是一个n维特征向量,![]() 是样本
是样本![]() 的类别标记。
的类别标记。
目标:学得一组n维原型向量![]() ,每个原型向量代表一个聚类簇,簇标记
,每个原型向量代表一个聚类簇,簇标记![]() 。
。
过程:
- 初始化一组原型向量
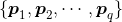
- 循环迭代(直到满足最大的运算轮数或调整幅度小于阈值)。
- 随机选择一个样本,找出距离该样本最近的一个原型向量,依据两者类别的标记是否一致来更新原型向量
原型向量的更新:
- 若最近的原型向量
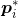 与
与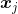 的类别标记相同,则令
的类别标记相同,则令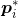 向
向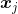 的方向靠拢,此时原型向量:
的方向靠拢,此时原型向量:
-
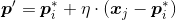
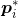 与
与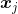 之间的距离
之间的距离- 令学习率
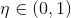 ,则原型向量
,则原型向量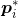 在更新为
在更新为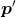 之后将更接近
之后将更接近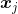
-
- 若最近的原型向量
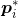 与
与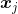 的类别标记不同,则令
的类别标记不同,则令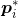 远离
远离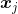 的方向,此时原型向量:
的方向,此时原型向量:
-
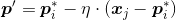
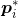 与
与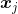 之间的距离
之间的距离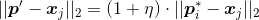
- 令学习率
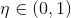 ,则原型向量
,则原型向量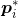 在更新为
在更新为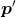 之后将更远离
之后将更远离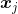
-
高斯混合聚类
与kmeans、LVQ用原型向量刻画聚类结构不同,高斯混合聚类采用概率模型来表达聚类原型。
多元高斯分布,对n维样本空间![]() 中的随机向量
中的随机向量![]() ,若
,若![]() 服从高斯分布,其概率密度函数:
服从高斯分布,其概率密度函数:
其中,![]() 谁n维均值向量,
谁n维均值向量,![]() 是
是![]() 的协方差矩阵,高斯分布完全由均值向量
的协方差矩阵,高斯分布完全由均值向量![]() 和协方差矩阵
和协方差矩阵![]() 这两个参数确定。为明确显示高斯分布与相应参数的依赖关系,将概率密度函数记为
这两个参数确定。为明确显示高斯分布与相应参数的依赖关系,将概率密度函数记为![]() ,这边只是一个记号,并不少是条件概率的意思,等价于(2)式中的
,这边只是一个记号,并不少是条件概率的意思,等价于(2)式中的![]() 。
。
定义高斯混合分布
该分布共由k个混合成分组成,每个混合成分对应一个高斯分布,其中![]() 与
与![]() 是第i个高斯混合成分的参数,而
是第i个高斯混合成分的参数,而![]() 为相应的“混合系数”,
为相应的“混合系数”,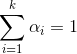
待续
4、密度聚类
密度聚类亦称“基于密度的聚类”,此类算法假设聚类结构能通过样本分布的紧密程度确定。通常性情下,密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。
DBSCAN是一种著名的密度聚类算法,它基于一组“邻域”参数![]() 来刻画样本分布的紧密程度。给定数据集
来刻画样本分布的紧密程度。给定数据集![]() ,定义
,定义
 -邻域:对
-邻域:对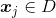 ,其
,其 -邻域包含样本集D中与
-邻域包含样本集D中与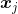 的距离不大于
的距离不大于 的样本,即
的样本,即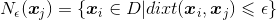
- 核心对象:若
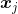 的
的 -邻域至少包含
-邻域至少包含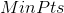 个样本,即
个样本,即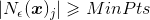 ,则
,则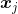 是一个核心对象
是一个核心对象 - 密度直达:若
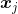 位于
位于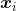 的
的 -邻域中,且
-邻域中,且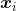 是核心对象,则称
是核心对象,则称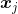 由
由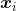 密度直达(密度直达通常不满足对称性,因为x必须有核心对象直达)
密度直达(密度直达通常不满足对称性,因为x必须有核心对象直达) - 密度可达:对
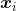 与
与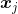 ,若存在样本序列
,若存在样本序列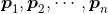 ,其中
,其中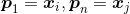 且
且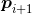 由
由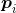 密度直达,则称
密度直达,则称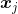 由
由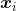 密度可达(密度可达满足直递性,不一定满足对称性,且密度可达还借助了密度直达的概念)
密度可达(密度可达满足直递性,不一定满足对称性,且密度可达还借助了密度直达的概念) - 密度相连:对
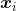 与
与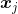 ,若存在
,若存在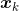 使得
使得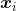 与
与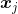 均由
均由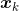 密度可达,则称
密度可达,则称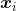 与
与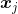 密度相连(密度相连满足对称性)
密度相连(密度相连满足对称性)
基于这些概念,DBSCAN将“簇”定义为:由密度可达关系导出的最大的密度相连样本集合。形式化的说,给定邻域参数![]() ,簇
,簇![]() 是满足以下性质的非空样本子集:
是满足以下性质的非空样本子集:
- 连接性:
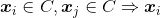 与
与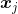 密度相连
密度相连 - 最大性:
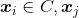 由
由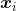 密度可达
密度可达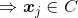
那么如何从D中找出满足以上性质的聚类簇呢?实际上,若![]()
![]() 为核心对象,由
为核心对象,由![]() 密度可达的所有样本组成的集合记为
密度可达的所有样本组成的集合记为![]() 由
由![]() 密度可达
密度可达![]() ,则不难证明X即为满足连接性和最大性的簇。
,则不难证明X即为满足连接性和最大性的簇。
过程:
- 找出样本中的所有核心对象集合

- 初始化现有聚类簇数k=0,初始化为访问样本集合为整个样本
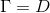
- 循环迭代直至满足条件(直到访问过所有的核心对象)
- 随机选取一个核心对象并入队
- 当队列不为空,弹出队首元素,并寻找其
 -邻域中所有未访问过的样本
-邻域中所有未访问过的样本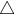 ,若其中有核心对象就入队并且更新未访问过的样本
,若其中有核心对象就入队并且更新未访问过的样本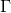 (将
(将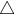 从为访问过的样本中剔除)
从为访问过的样本中剔除)
- 当队列不为空,弹出队首元素,并寻找其
- 生成第k个聚类簇(两个集合的差集即使聚类簇,
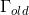 上一轮未访问样本集合,
上一轮未访问样本集合,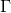 这一轮未访问样本集合),更新现有聚类簇数k=k+1
这一轮未访问样本集合),更新现有聚类簇数k=k+1 - 更新未访问过的核心对象集合
 (将已访问的剔除)
(将已访问的剔除)
- 随机选取一个核心对象并入队
5、层次聚类
层次聚类试图在不同层次对数据集进行划分,从而形成树形的聚类结构,数据集的划分可采用“自底向上”的聚合策略,也可采用“自顶向下”的分拆策略。即凝聚式层次聚类:在初始阶段将每个店都视为一个簇,之后合并两个最接近的簇,直到最后只剩一个簇;分裂式层次聚类:在初始阶段将所有点视为一个点,之后每分裂出一个簇,直到最后剩下单个点的簇。
AGNES是一种采用自底向上聚合策略的层次聚类算法,他先将数据集中的每个样本看做一个初始聚类簇,然后在算法运行的每一步找出距离最近的两个聚类簇进行合并,该过程不断重复,直到达到预设的聚类簇个数。这里关键是素和计算聚类簇之间得距离,实际上,每个簇是一个样本集合,因此,只需要采用关于集合的某种距离即可。
⚠️:感觉图中17和18行之间缺少了一个外层循环,距离矩阵更新应该两层循环,然后还有既然用了对称性,内层循环j只要从i+1开始就可以了。
过程:
- 初始化,将每个样本当作一个初始聚类簇,并对相应的距离矩阵进行初始化
- 循环迭代直至满足退出条件(达到预设的聚类簇数)
- 找出距离最近的两个聚类簇
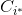 和
和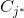 ,将这两个聚类簇合并成
,将这两个聚类簇合并成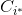
- 因为少了一个聚类簇,故距离矩阵需要删掉第
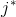 行和第
行和第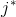 列,并且将聚类簇的编号重编(
列,并且将聚类簇的编号重编(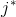 之后的因为删掉了
之后的因为删掉了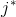 ,所以均往前挪一个)
,所以均往前挪一个) - 对现在的q-1个聚类簇,重新计算距离矩阵。
- 找出距离最近的两个聚类簇
参考:机器学习,周志华