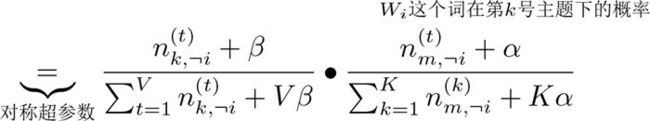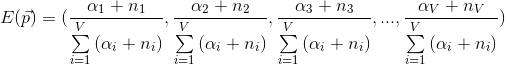LDA-模型的实现-----吉布斯采样
https://www.cnblogs.com/nlp-yekai/p/3858705.html?utm_source=tuicool&utm_medium=referral
算法 LDA Collapsed Gibbs Sampling
输入：文档集(分词后)，K(主题数)，α，β，iter_number(迭代次数)
输出：θ_mat(doc->topic)和
(topic->word)、tassign文件(topic assignment）
对于中文语料要首先分词，给定K个主题数目，alpha，beta和迭代次数的确定
输出：theta_mat(doc->topic)和phi_mat(topic->word),主题分布的文件
定义的统计量：
nw[][]:单词i分配给主题j，大小为V*K（词典的大小*主题个数）
nwsum[]:主题j中的单词数目，大小 为k
nd[][]:第i篇文档里被 指定第j个主题词的次数，大小为:M*K（文档数目*主题个数）
ndsum[]:文档i中的单词。大小为M
z[][]:每个单词的主题分布，大小为M*每篇文档的单词数(第M文档中第n个词被指定的主题的索引)
初始化阶段：
循环1：文档数目m
循环2：文档中的单词数目n
(topic_index)主题_索引=主题随机指定
z[m][n]=topic_index
nw[word_id][topic_index]=++
nwsum[topic_index]++
nd[m][ topic_index]++
ndsum[m]++
初始化结束后的迭代重新采样的三部曲-1→采样公式重新分配+1→三重奏
collasped of Gibbs Sampling迭代阶段：(每次迭代有三个for循环)
for iter in iter_number{ //迭代iter_number次
for (m, doc) in doc_set{ //m是doc编号，文档的编号
for word in doc{ #文档中的单词
t=从z[m][n]中取得当前word的主题编号(初始化来自随机)
令nw[word_id][t]、nwsum[t]、nd[m][t]三个统计量均−1 (-1三部曲的第一步)
double p[] = new double p[K]
for k in [0,1,2,...,K-1]{ //从0到K-1号每个主题计算概率
每个单词产生的概率估计值是对应事件的先验的伪计数和数据中的计数的和在整体计数中的比例
两个图可以进行对比说明。
//按照上述公式生成每个主题的概率存到临时概率数组p中
}
new_t = 输入数组p到算法4.1 cumulative method随机投掷 #产生的新的主题 ----采样是从该式体现出来
令nw[word_id][new_t]、nwsum[new_t]、nd[m][new_t]三个统计量均+1
}
}
}
输出阶段(也可以在迭代一半时候即可输出):
根据z数组输出文件tassign.txt
根据nw、nwsum、nd、ndsum套用公式(3.4)生成文件theta.txt和文件phi.txt
文件theta格式: 大矩阵文件,M行K列
文件phi格式: 大矩阵文件,K行V列
model文件就是算法4.2输出的这几个矩阵文件。如果输出了这几个文件,中断训练后,下次想再继续的时候:nw、nwsum、nd、ndsum这4
个统计量均从tassign文件中可以读取得到。
预测(predict):
另外,如果已经训练过一个model了,如果有一篇新文档,需要对其predict(预测)新文档上的主题分布,可以利用已经训练的trn_nw和trn_nwsum用以下公式推断,
trn_nw和trn_nwsum相当于起到了伪计数(pseudo count)的作用,公式后一项因子只与当前文档的主题词数计数有关,故不必加入已有训练过的(train)model的计数。此外,预测(predict)在不管是初始化还是迭代时只修改new_nw和new_nwsum统计量,其余采样过程都一样
由于trn_nw二维数组变量已经很大,因此new_nw变量对其影响不是特别的大,所以可以减少一些对文档预测时候的采样次数,通常情
况下,20次采样足矣。
-1→重新分配topic→+1三重奏,我将其形象比喻为在采样每个单词前,从各个统计量中抠掉该单词(及其主题),然后重新分
1.tassign文件(一行一个doc,冒号前是wordid,冒号后是topicid)
2.theta文件(矩阵文件:行号=doc idx,列号=topic idx)
3.phi文件(矩阵文件:行号=topic idx,列号=word idx)
4.wordmap文件(word→wordid)
nd[]----------------theta