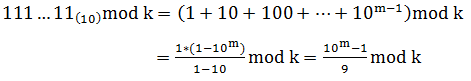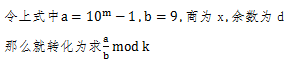2016"百度之星" - 初赛（Astar Round2A）解题报告

此文章可以使用目录功能哟↑(点击上方[+])

有点智商捉急,第一题卡了好久,看来不服老,不服笨是不行的了...以下是本人目前的题解,有什么疑问欢迎提出

链接→2016"百度之星" - 初赛（Astar Round2A）

 Problem 1001 All X

Accept: 0    Submit: 0
Time Limit: 2000/1000 mSec(Java/Others)    Memory Limit : 65536 KB

 Problem Description

F(x,m) 代表一个全是由数字x组成的m位数字。请计算，以下式子是否成立：

       F(x,m) mod k ≡ c

 Input

      第一行一个整数T，表示T组数据。 每组测试数据占一行，包含四个数字x,m,k,c

1≤x≤9

1≤m≤10,000,000,000
​​ 

0≤c

 Output

对于每组数据，输出两行： 第一行输出："Case #i:"。i代表第i组测试数据。 第二行输出“Yes” 或者 “No”，代表四个数字，是否能够满足题目中给的公式。

 Sample Input

3
1 3 5 2
1 3 5 1
3 5 99 69

 Sample Output

Case #1:
No
Case #2:
Yes
Case #3:
Yes

Hint

对于第一组测试数据：111 mod 5 = 1，公式不成立，所以答案是”No”，而第二组测试数据中满足如上公式，所以答案是 “Yes”。

 Problem Idea

解题思路:此题求的是m个数字x组成的m位数对k取模是否等于c,从m的大小可以看出此题想利用同余定理1位1位计算是解决不了了,这样我们就得换种思路,首先,我们提取一个x,那剩下的就是m个1,如下:

这个数要mod k ,那这个数应该怎么表示呢?

就这样转化了,然后10^m可以通过快速幂解决,但是很明显,除以9操作怎么办,除法取模,余数是会改变的,逆元?但是9和k不一定互质,且k也不一定是质数,所以扩展欧几里得和费马小定理都不能用了,束手无策

好吧,这里提供一种小方法

就这样经过几步转化,我求d不需要进行除法取模了,那我上面的问题不就解决了?对的

在这里,我要提一点更优化的操作(虽然此题优化效果不是太明显)

首先我们知道欧拉定理

φ(k)为欧拉函数,表示k以内与k互质的数的个数

而我们在求解10^m的时候就可以借用欧拉定理降幂

不好意思,上面的欧拉定理降幂误导了大家,欧拉定理成立是有条件的,即a与k需要互质,本题10与k不一定互质

只能说题目数据才水,本人考虑不周,不过去掉欧拉定理这部分,代码还是对的,降幂这点小优化没有还可以靠快速幂弥补,不要紧

题目链接→HDU 5690 All X

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include

 Problem 1002 Sitting in Line

Accept: 0    Submit: 0

Time Limit: 10000/5000 mSec(Java/Others)    Memory Limit : 262144 KB

 Problem Description

度度熊是他同时代中最伟大的数学家，一切数字都要听命于他。现在，又到了度度熊和他的数字仆人们玩排排坐游戏的时候了。游戏的规则十分简单，参与游戏的N个整数将会做成一排，他们将通过不断交换自己的位置，最终达到所有相邻两数乘积的和最大的目的，参与游戏的数字有整数也有负数。度度熊为了在他的数字仆人面前展现他的权威，他规定某些数字只能在坐固定的位置上，没有被度度熊限制的数字则可以自由地交换位置。

 Input

     

第一行一个整数T，表示T组数据。 每组测试数据将以如下格式从标准输入读入：​​ 

第一行，整数N(1≤N≤16)，代表参与游戏的整数的个数。从第二行到第 (N + 1)行，每行两个整数，ai(−10000≤a​i≤10000)、p​i(p​i=−1 或 0≤p​i

 Output

第一行输出："Case #i:"。i代表第i组测试数据。

第二行输出数字重新排列后最大的所有相邻两数乘积的和，即

 Sample Input

2
6
-1 0
2 1
-3 2
4 3
-5 4
6 5
5
40 -1
50 -1
30 -1
20 -1
10 -1

 Sample Output

Case #1:
-70
Case #2:
4600

 Problem Idea

解题思路:要求,很显然是道DP题

首先我们假设dp[1<<16][16],第一维可以表示成一个16位二进制数,其中,二进制数的第i位如果为1表示a[i]已经选择好放的位置,否则即a[i]还没有选定位置;dp数组第二维表示该序列目前以a[i]结尾

故dp[i][j]就表示在状态i下,以a[j]结尾的序列的值

对于dp[i][j],i这个状态已经填了x个数(x为i的二进制表示下1的个数),我们准备填第x+1个数时,如果当前位置必填某个数,那么,就只更新以规定的这个数结尾转移方程如果没有那就枚举那么可以任意放的数来更新相应的状态及答案

故而可以得到转移方程

dp还是比较难理解的,有什么不明白的地方,欢迎咨询

题目链接→HDU 5691 Sitting in Line

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include

 Problem 1005 BD String

Accept: 0    Submit: 0

 Time Limit: 2000/1000 mSec(Java/Others)    Memory Limit : 65536 KB

 Problem Description

众所周知，度度熊喜欢的字符只有两个：B和D。

今天，它发明了一种用B和D组成字符串的规则：

S(1)=B

S(2)=BBD

S(3)=BBDBBDD

…

S(n)=S(n-1)+B+reverse(flip(S(n-1))

其中，reverse(s)指将字符串翻转，比如reverse(BBD)=DBB，flip(s)指将字符串中的B替换为D，D替换为B，比如flip(BBD)=DDB。

虽然度度熊平常只用它的电脑玩连连看，这丝毫不妨碍这台机器无与伦比的运算速度，目前它已经算出了S()的内容，但度度熊毕竟只是只熊，一次读不完这么长的字符串。它现在想知道，这个字符串的第L位（从1开始）到第R位，含有的B的个数是多少？

 Input

第一行一个整数T，表示T(1≤T≤1000) 组数据。每组数据包含两个数L和R(1≤L≤R≤ ) 。

 Output

对于每组数据，输出S()表示的字符串的第L位到第R位中B的个数。

 Sample Input

3
1 3
1 7
4 8

 Sample Output

2
4
3

 Problem Idea

解题思路:从字符串规则可以看出以下几点

①S(n)的串长度为;

②S(n)中B的个数为个(以正中间的B为中心,假设左边有x个B,那么右边有个,即左边B的个数+右边B的个数=S(n-1)的串长度)

③远大于,故只是吓唬我们的

由上述几点可知,此题并没有表面上那么吓人

要求区间[l,r]内B的个数,我们可以转化为求[1,r]-[1,l-1]

而求区间[1,x]内B的个数,又可以如上述第②条所说,拆成3段,递归求解

比如x=12时,S=BBDBBDDBBBDD……

拆成3段如下:

右边4个是多余的,但是因为右边是由reverse+flip得到的,求右边4个中B的个数可以转化成求4-([1,7]中B的个数-[1,3]中B的个数)

而[1,3]中的个数又是得递归求解的

这题递归讲得比较绕,要是小伙伴没明白的,可以留下评论,我会及时回复的

题目链接→HDU 5694 BD String

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include

 Problem 1006 Gym Class

Accept: 0    Submit: 0 

Time Limit: 6000/1000 mSec(Java/Others)    Memory Limit : 65536 KB

 Problem Description

众所周知，度度熊喜欢各类体育活动。

今天，它终于当上了梦寐以求的体育课老师。第一次课上，它发现一个有趣的事情。在上课之前，所有同学要排成一列， 假设最开始每个人有一个唯一的ID，从1到N，在排好队之后，每个同学会找出包括自己在内的前方所有同学的最小ID，作为自己评价这堂课的分数。麻烦的是，有一些同学不希望某个（些）同学排在他（她）前面，在满足这个前提的情况下，新晋体育课老师——度度熊，希望最后的排队结果可以使得所有同学的评价分数和最大。

 Input

第一行一个整数T，表示T(1≤T≤30) 组数据。对于每组数据，第一行输入两个整数N和M (1≤N≤100000,0≤M≤100000)，分别表示总人数和某些同学的偏好。接下来M行，每行两个整数A 和B(1≤A,B≤N)，表示ID为A的同学不希望ID为B的同学排在他（她）之前。你可以认为题目保证至少有一种排列方法是符合所有要求的。

 Output

对于每组数据，输出最大分数 。

 Sample Input

3
1 0
2 1
1 2
3 1
3 1

 Sample Output

1
2
6

 Problem Idea

解题思路:众所周知,为了使每个人给的评分尽可能高,在没有条件的情况下,必定是ID高的排前面来得最优

但是度度熊没有那么善良

ID为B的同学不能排在A前面,好吧,怎么做呢?

对于这种调度问题,我们不妨用拓扑排序来求解

假设B不能排在A前面,那么我就在AB之间画一条从A指向B的边,那么我们可以得到一幅有向图

我们要按ID从大往小排,同时要考虑当前这位同学是否有特殊要求

上面有向图中,凡入度为0的结点,表示没有同学不希望该同学排在它的前面,故该同学可以按照ID从大往小排

所以此题的做法是,每次将入度为0的结点放入优先队列中,选取ID最大的结点先排,然后将该ID的同学讨厌的所有同学入度-1,若入度变为0同样要放入优先队列判断ID先后,这里建图可以邻接表实现,也可以利用一些vector

题目链接→HDU 5695 Gym Class

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include

菜鸟成长记