leetcode刷题笔记(2)
目录
1. Two Sum
15. 3Sum
18. 4Sum
22. 括号生成
23. Merge k Sorted Lists
array专题:
26. 删除排序数组中的重复项
80. 删除排序数组中的重复项 II
82. 删除排序链表中的重复元素 II
88. Merge Sorted Array 合并有序数组
LeetCode: 36. Valid Sudoku(检测一个9x9矩阵是不是数独)(用HashSet做)
37. Sudoku Solver (数独问题)
51. N-Queens
String专题:
28. Implement strStr()
矩阵专题:
48. Rotate Image
29 Divide Two Integers
69. Sqrt(x)
1. Two Sum
给定一个整数数组
nums和一个目标值target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9 因为 nums[0] + nums[1] = 2 + 7 = 9 所以返回 [0, 1]
思路:
1.一般的方法就是遍历一遍数组,然后向前查找一个数,要求这个数与当前遍历到到数相加为target。时间复杂度O(n^2)
2.在思路1的基础上用hashMap,存储以前遍历过的数,这样就可以用O(1)的时间查找符合要求的数。以空间换时间。time:O(n),space:O(n)
public int[] twoSum(int[] numbers, int target) {
int[] result = new int[2];
Map map = new HashMap();
for (int i = 0; i < numbers.length; i++) {
if (map.containsKey(target - numbers[i])) {
result[1] = i + 1;
result[0] = map.get(target - numbers[i]);
return result;
}
map.put(numbers[i], i + 1);
}
return result;
} 3.先对数组排个序,然后用双指针法,若相等,则要把这对结果保存进队列中。若不想等,则移动两个指针。这个方法用在了3sum和4sum中。
15. 3Sum
给定一个包含 n 个整数的数组
nums,判断nums中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。注意:答案中不可以包含重复的三元组。
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4], 满足要求的三元组集合为: [ [-1, 0, 1], [-1, -1, 2] ]
总体思路:先对数组排序,然后用双指针法,检查low和high相加是否等于target,若相等,则要把这对结果保存进队列中(因为题目说要求出所有的满足条件的值,所以要保存结果)。若不想等,则移动两个指针。
其实就是用了个for循环选出一个数,然后用target - 这个数 == 新的target。核心算法还是2sum的解法3
class Solution {
public List> threeSum(int[] num) {
Arrays.sort(num);
List> res = new LinkedList<>();
for (int i = 0; i < num.length-2; i++) {
if (i == 0 || (i > 0 && num[i] != num[i-1])) {
int lo = i+1, hi = num.length-1, sum = 0 - num[i];
while (lo < hi) {
if (num[lo] + num[hi] == sum) {
res.add(Arrays.asList(num[i], num[lo], num[hi]));
while (lo < hi && num[lo] == num[lo+1]) lo++;
while (lo < hi && num[hi] == num[hi-1]) hi--;
lo++; hi--;
} else if (num[lo] + num[hi] < sum) lo++;
else hi--;
}
}
}
return res;
}
} 18. 4Sum
Given an array
numsof n integers and an integertarget, are there elements a, b, c, and dinnumssuch that a + b + c + d =target? Find all unique quadruplets in the array which gives the sum oftarget.Note:
The solution set must not contain duplicate quadruplets.
Example:
Given array nums = [1, 0, -1, 0, -2, 2], and target = 0. A solution set is: [ [-1, 0, 0, 1], [-2, -1, 1, 2], [-2, 0, 0, 2] ]
先要想到朴素算法是怎样算的。这涉及到一个基础问题,怎么选出一个数组中的四个不同的无序的数,就是用四重for循环。因为这题用了双指针,简化了两重for循环,进而优化了算法。
总结一下就是:在双指针算法上套了两层for循环。
22. 括号生成
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
[ "((()))", "(()())", "(())()", "()(())", "()()()" ]
recursion专题
public List generateParenthesis(int n) {
List list = new ArrayList();
generateOneByOne("", list, n, n);
return list;
}
public void generateOneByOne(String sublist, List list, int left, int right){
if(left > right){
return;
}
if(left > 0){
generateOneByOne( sublist + "(" , list, left-1, right);
}
if(right > 0){
generateOneByOne( sublist + ")" , list, left, right-1);
}
if(left == 0 && right == 0){
list.add(sublist);
return;
}
} 23. Merge k Sorted Lists
Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.
Example:
Input: [ 1->4->5, 1->3->4, 2->6 ] Output: 1->1->2->3->4->4->5->6
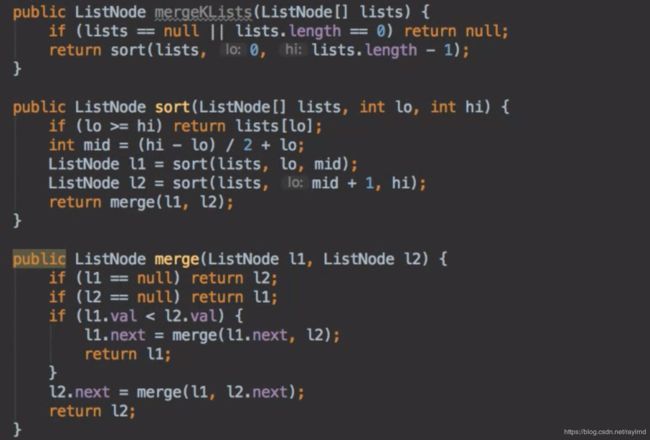
1.这题的思路就是利用归并排序的算法,以merge()作为子过程,处理一遍List。merge()把两个List合并成一个有序的List。
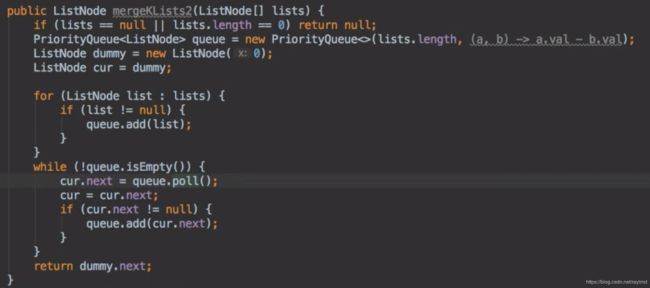
2.方法二:
优先队列法,优先队列的规则是按node值小的排在前面。
比如说:
node1: 6 -> 2 -> 3
node2: 2 -> 4
node3: 4 -> 5
先把所有的list都加到优先队列中,然后从优先队列中取出一个数,即头节点值最小的链表,然后用cur指向它,然后把cur的next加入优先队列。如此进行,直到优先队列为空。
优先队列中的数的分布情况变化图:
2->5->10
4->8
6->7->9
-------- 把2拿走
4->8
5->10
6->7->9
--------把4拿走
5->10
6->7->9
8
-------把5拿走
6->7->9
8
10
-----把6拿走
7->9
8
10
------把7,8,9,10拿走
cur : 2->4->5->6->7->8->9->10
array专题:
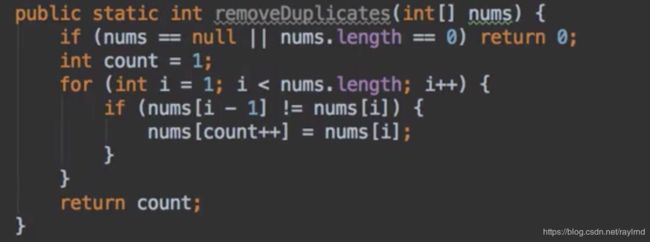
26. 删除排序数组中的重复项
删除数组中的元素,从本质上来说就是把重复元素的下一个数字赋值给第二个重复元素的位置。那么就可以分解为两个子问题,把什么值赋值给什么值。就比如说:
| 数组元素 | 1 | 1 | 1 | 2 | 2 | 3 | 4 |
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
把下标3的元素2赋值给下标1的元素1,那么数组变为:1,2,1,2,2,3,4
把下标5的元素3赋值给下标2的元素2,那么数组变为:1,2,3,2,2,3,4
把下标6的元素4赋值给下标3的元素2,那么数组变为:1,2,3,4,2,3,4
80. 删除排序数组中的重复项 II
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素最多出现两次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定 nums = [1,1,1,2,2,3], 函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为1, 1, 2, 2,3 。
题目要求最多出现两次。逆向思维,所以这题关注的焦点是如何防止超过两个重复的数出现(破坏三个数同时出现的条件,即nums[i-2] == nums[i])。这样一来,第0,1位置就不用检查了,因为反正不会超过三个数,就算两个数一样也没事。也就是说如果nums[i] != nums[i-2],那么在[ i - 2 , i ]一定不会有三个一样的数出现,那么就要把它赋值给count变量指向的位置.
注意:这题的输入数组是有序。
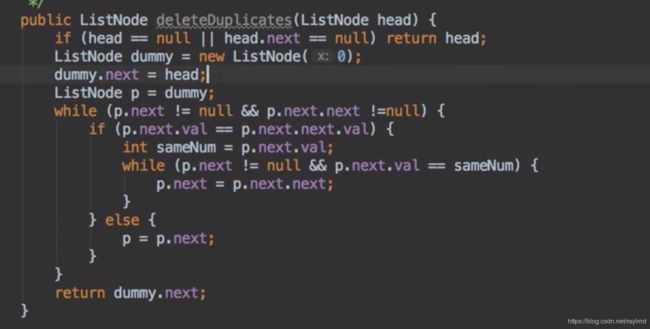
82. 删除排序链表中的重复元素 II
遇到重复的元素,先把重复的元素的值保存下来,然后向后扫描节点,如果后续节点与重复的值相同,则删除该节点,如果不同,则向后移动。
88. Merge Sorted Array 合并有序数组
Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.
Note:
- The number of elements initialized in nums1 and nums2 are m and n respectively.
- You may assume that nums1 has enough space (size that is greater or equal to m + n) to hold additional elements from nums2.
Example:
Input:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
Output: [1,2,2,3,5,6]给两个有序的数组 A 和 B,把 B 合并到 A,变成一个数组,假定 A 有足够的空间。
可以考虑新建立一个m + n的数组,然后从两个数组的开头取各取一个元素进行比较,把小的放进新数组,然后在循环这个过程,直到结束。
好的方法是不用新建立数组,而是直接在A 数组上写入,因为 A 足够大,可从两个数组的最大数也就是最后一个数开始比较,大的写入A[m + n -1],然后循环这个过程。如果 B 的元素写完了,A 剩下的元素正好在正取的位置,不用写了。如果 A 的元素都取完了,那剩下的 B 的元素可一次全部写进 A。
LeetCode: 36. Valid Sudoku
Determine if a Sudoku is valid, according to: Sudoku Puzzles - The Rules.
The Sudoku board could be partially filled, where empty cells are filled with the character ‘.’.

A partially filled sudoku which is valid.
Note:
A valid Sudoku board (partially filled) is not necessarily solvable. Only the filled cells need to be validated.
大意是说: 判断给定的矩阵是否满足每行、每列、每个3*3的小矩阵中没有重复的数字(1-9)。
思路:用二维数组来充当hash表存储键值对,用row[i][c]存储 i -> c 键值对,用col[j][c]来存储 j -> c 键值对。block[i/3][j/3][c]用来存储 (i/3 , j/3 , c).
class Solution {
public:
bool isValidSudoku(vector>& board) {
int i, j, c;
int row[9][9], col[9][9], block[3][3][9];
memset(row, 0, sizeof(row));
memset(col, 0, sizeof(col));
memset(block, 0, sizeof(block));
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
if(board[i][j] != '.'){
c = board[i][j] - '1';
if (row[i][c] || col[j][c] || block[i / 3][j / 3][c])
return false;
else {
row[i][c] ++;
col[j][c] ++;
block[i / 3][j / 3][c]++;
}
}
}
}
return true;
}
}; 用HashSet原理跟上面的方法一样:
public class Solution {
public boolean isValidSudoku(char[][] board) {
HashSet[] row = new HashSet[9];
HashSet[] col = new HashSet[9];
HashSet[] cell = new HashSet[9];
for (int i = 0; i < 9; i++) {
row[i] = new HashSet();
col[i] = new HashSet();
cell[i] = new HashSet();
}
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') {
if (row[i].contains(board[i][j])
|| col[j].contains(board[i][j])
|| cell[3 * (i / 3) + j / 3].contains(board[i][j]))
return false;
else {
row[i].add(board[i][j]);
col[j].add(board[i][j]);
cell[3 * (i / 3) + j / 3].add(board[i][j]);
}
}
}
}
return true;
}
} 37. Sudoku Solver
编写一个程序,通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则:
- 数字
1-9在每一行只能出现一次。- 数字
1-9在每一列只能出现一次。- 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。空白格用
'.'表示。
一个数独。
答案被标成红色。
Note:
- 给定的数独序列只包含数字
1-9和字符'.'。- 你可以假设给定的数独只有唯一解。
- 给定数独永远是
9x9形式的。
回溯法
public class Solution {
public void solveSudoku(char[][] board) {
if(board == null || board.length == 0) return;
solve(board);
}
public boolean solve(char[][] board){
for(int i=0; i51. N-Queens
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens' placement, where
'Q'and'.'both indicate a queen and an empty space respectively.Example:
Input: 4 Output: [ [".Q..", // Solution 1 "...Q", "Q...", "..Q."], ["..Q.", // Solution 2 "Q...", "...Q", ".Q.."] ] Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.
返回所有可能的结果
class Solution {
public:
std::vector > solveNQueens(int n) {
std::vector > res;
std::vector nQueens(n, std::string(n, '.'));
solveNQueens(res, nQueens, 0, n);
return res;
}
private:
void solveNQueens(std::vector > &res, std::vector &nQueens, int row, int &n) {
if (row == n) {
res.push_back(nQueens);
return;
}
for (int col = 0; col != n; ++col)
if (isValid(nQueens, row, col, n)) {
nQueens[row][col] = 'Q';
solveNQueens(res, nQueens, row + 1, n);
nQueens[row][col] = '.';
}
}
bool isValid(std::vector &nQueens, int row, int col, int &n) {
//check if the column had a queen before.
for (int i = 0; i != row; ++i)
if (nQueens[i][col] == 'Q')
return false;
//check if the 45° diagonal had a queen before.
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; --i, --j)
if (nQueens[i][j] == 'Q')
return false;
//check if the 135° diagonal had a queen before.
for (int i = row - 1, j = col + 1; i >= 0 && j < n; --i, ++j)
if (nQueens[i][j] == 'Q')
return false;
return true;
}
}; String专题:
28. Implement strStr()
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例 1:
输入: haystack = "hello", needle = "ll" 输出: 2示例 2:
输入: haystack = "aaaaa", needle = "bba" 输出: -1

矩阵专题:
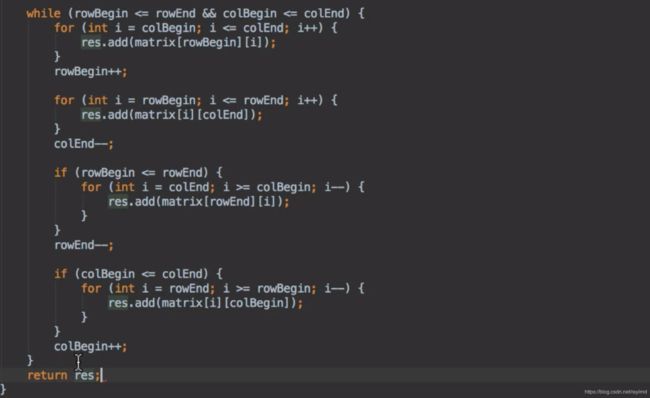
54. Spiral Matrix
问题描述
给出一个 m x n 的矩阵(m 行, n 列),请按照顺时针螺旋顺序返回元素。例如,给出以下矩阵:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
应该返回 [1,2,3,6,9,8,7,4,5]解题思路和分析
方法一:模拟
直觉就是按照这个顺时针的顺序将数组中的数字输出。
方法一:由外到内逐层遍历法(笔试时掌握这种写法就可以了,方法二只是作为了解)
先输出最外层元素,再输出第二层的元素,以此类推。
时间复杂度:O(n),n为矩阵中元素的数量,因为要把矩阵的每个元素添加到我们的结果中(ans);
空间复杂度:O(n),存储ans
方法二:用数组来管理指针的移动方向,用visit数组来防止边界转弯问题
矩阵有R行,C列,seen[r][c]数组用来标记是否被访问过。我们现在的位置是[r][c],前进的方向是di,我们要把数组内的所有元素都访问一遍。
当我们在数组内移动的时候,我们候选的下一个位置是(cr,cc)。如果(cr,cc)属于这个矩阵并且还没有被访问过,那么我们就移动到(cr,cc)。否则,我们应该顺时针转弯了,即让di在dr和dc数组中后移一位,di++.
dr和dc数组的含义:
dr表示行移动的方向,dc表示列移动的方向。
红色部分,r不移动,c向下移动一位,c += dc[di];
绿色部分,c不移动,r向下移动一位, r += dr[di];
class Solution {
public List spiralOrder(int[][] matrix) {
List ans = new ArrayList(); //存储结果
if (matrix.length == 0) return ans;
int R = matrix.length, C = matrix[0].length; //R行C列
boolean[][] seen = new boolean[R][C]; //boolean数组用来标记是否被访问过
int[] dr = {0, 1, 0, -1}; //表示方向
int[] dc = {1, 0, -1, 0};
int r = 0, c = 0, di = 0;
for (int i = 0; i < R * C; i++) {
ans.add(matrix[r][c]);
seen[r][c] = true;
int cr = r + dr[di];
int cc = c + dc[di];
if (0 <= cr && cr < R && 0 <= cc && cc < C && !seen[cr][cc]){
r = cr;
c = cc;
} else {
di = (di + 1) % 4;
r += dr[di];
c += dc[di];
}
}
return ans;
}
}
时间复杂度:O(n),n为矩阵中元素的数量,因为要把矩阵的每个元素添加到我们的结果中(ans);
空间复杂度:O(n),n为矩阵中元素的数量,seen和ans;
---------------------
转自原文:https://blog.csdn.net/Regemc/article/details/79714003
48. Rotate Image
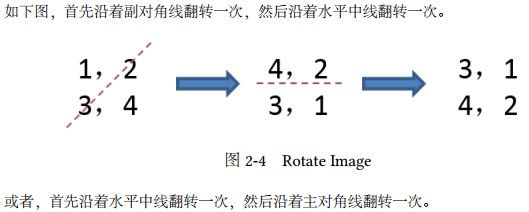
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
给定 matrix = [ [1,2,3], [4,5,6], [7,8,9] ], 原地旋转输入矩阵,使其变为: [ [7,4,1], [8,5,2], [9,6,3] ]示例 2:
给定 matrix = [ [ 5, 1, 9,11], [ 2, 4, 8,10], [13, 3, 6, 7], [15,14,12,16] ], 原地旋转输入矩阵,使其变为: [ [15,13, 2, 5], [14, 3, 4, 1], [12, 6, 8, 9], [16, 7,10,11] ]
void rotate(vector>& matrix) {
int n = matrix.size();
// 沿着副对角线反转
for(int i = 0; i < n; i++)
for(int j = 0; j < n -i ; j++)
swap(matrix[i][j],matrix[n-j-1][n-i-1]);
//沿着水平中轴上下交换
for(int i = 0; i < n/2; i++)
for(int j = 0; j < n ; j++)
swap(matrix[i][j],matrix[n-i-1][j]);
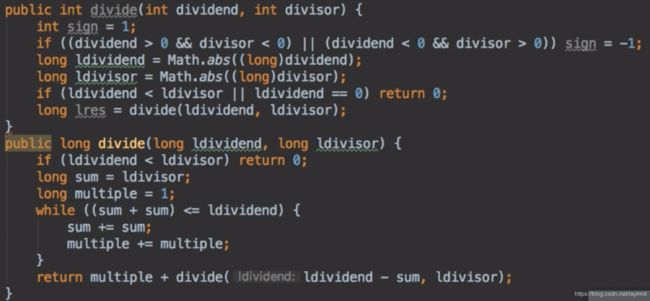
} 29 Divide Two Integers
被除数 ldividend = 10, 除数ldivisor = 3. 求 ldividend / ldivisor = 3
3*2 < 10 < 3*3
用multiple记录商的增加,用sum来记被除数的增加,随着sum的每次扩张,multiple也会跟着增加,当sum增加到除数ldivisor时停止增加。
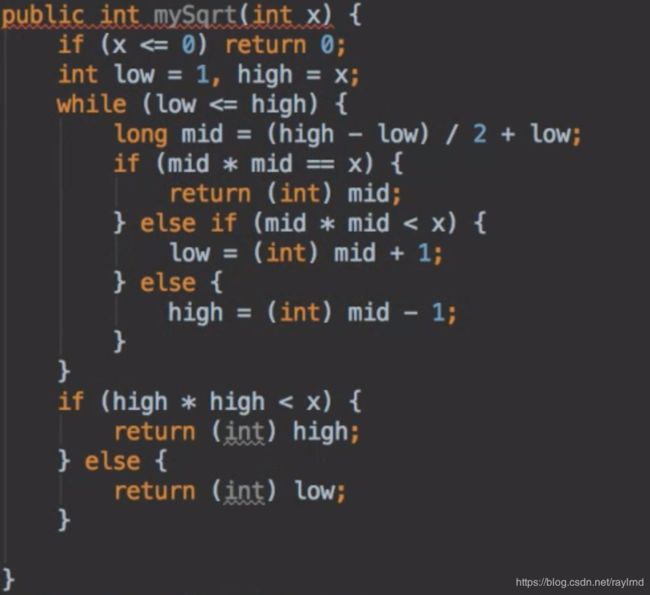
69. Sqrt(x)
实现
int sqrt(int x)函数。计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4 输出: 2示例 2:
输入: 8 输出: 2 说明: 8 的平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
因为while循环执行完后,low > high。其实最后一步可以不用if else判断,直接返回high即可。为了避免思考细节问题,写个判断语句。