XGBoost 2 - 机器学习基础

2 - 机器学习基础

• 监督学习
• 分类回归树
• 随机森林

2.1 - 监督学习

• 模型
• 参数
• 目标函数
  
  • 损失函数
  • 正则项
• 优化

2.1.1 - 模型

若y为离散值，则为分类问题；若y为连续值，则为回归问题。

对于给定的x如何预测标签 y^ y ^ ?
- 对于回归问题中的线性回归，其模型为：

y^=f(x)=∑jwjxj y ^ = f ( x ) = ∑ j w j x j

- 对于二类分类问题 y∈{0,1} y ∈ { 0 , 1 } ，其模型 f(x)=p(y=1|x) f ( x ) = p ( y = 1 | x ) ，即该模型想要拟合的是样本 x x 是正例（ y=1 y = 1 ）的概率。

y^=θ(z)=11+exp(−z)=11+exp(−∑jwjxj) y ^ = θ ( z ) = 1 1 + e x p ( − z ) = 1 1 + e x p ( − ∑ j w j x j )

2.1.2 - 目标函数

求解模型的参数：构建一个目标函数，然后最小化该目标函数。

J(w)=1N∑n=1NL(yn,yn^)+λΩ(w) J ( w ) = 1 N ∑ n = 1 N L ( y n , y n ^ ) + λ Ω ( w )

2.1.2.1 - 损失

• 损失函数-回归：

  • L2损失： L=12(y^−y)2 L = 1 2 ( y ^ − y ) 2 (受异常点影响大)
  • L1损失： L=|y^−y| L = | y ^ − y | (0处不可导)

• 损失函数-分类

  • 0/1损失：
    
    L(y,y^)={0, if y=y^1, if y≠y^ L ( y , y ^ ) = { 0 ,  if  y = y ^ 1 ,  if  y ≠ y ^

  • logistic损失/cross entropy loss/负log似然损失
    

    L(y,y^)=−ylogy^−(1−y)log(1−y^) L ( y , y ^ ) = − y l o g y ^ − ( 1 − y ) l o g ( 1 − y ^ )
    
    简单推导：

    log似然：

    l(θ)=log(likelihood(θ))=log(ΠNn=1p(y|x;θ))=∑n=1Nlog(p(y|x;θ)) l ( θ ) = l o g ( likelihood ( θ ) ) = l o g ( Π n = 1 N p ( y | x ; θ ) ) = ∑ n = 1 N l o g ( p ( y | x ; θ ) )
    
    所以最小化负log似然损失等价于最大化似然函数
    
    ==−∑n=1Nlog(p(y|x;θ))−∑n=1Nlog(y^y(1−y^)(1−y))−∑n=1Nylogy^+(1−y)log(1−y^)(18)(19)(20) (18) − ∑ n = 1 N l o g ( p ( y | x ; θ ) ) (19) = − ∑ n = 1 N l o g ( y ^ y ( 1 − y ^ ) ( 1 − y ) ) (20) = − ∑ n = 1 N y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ )

  • 合页损失：
    L=max{0,1−ys} L = m a x { 0 , 1 − y s }
  • 指数损失：
    L=exp(−ys) L = e x p ( − y s )

2.1.2.2 - 正则

• 不能只选择损失最小的模型，因为复杂的模型可能和训练数据拟合得非常好，在训练集上可以损失几乎为0，但测试数据和训练数据虽然是来自同分布的独立样本，但只是分布相同，随机变量取值会变化，这时在测试数据上的表现可能会变差
• 训练数据中可能会有噪声，模型不应该将噪声包含在内

所以需要控制模型复杂度，太过复杂的模型不能泛化/推广到新数据上：根据特定输入调制得太好，而不是真正建模x与y之间的关系。

正则项：对复杂模型施加惩罚

例子：

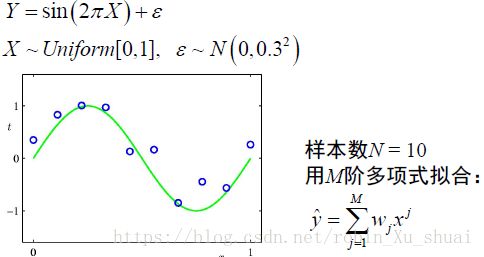
M为多项式的阶数。

增加了L2正则的线性回归，岭回归：

J(w,b)=1N∑n=1N(yn−(wTxn+b))2+λ∑j=1Mw2j J ( w , b ) = 1 N ∑ n = 1 N ( y n − ( w T x n + b ) ) 2 + λ ∑ j = 1 M w j 2

• L2正则： Ω(θ)=λ∥θ∥22=λ∑Dj=1θ2j Ω ( θ ) = λ ‖ θ ‖ 2 2 = λ ∑ j = 1 D θ j 2
• L1正则： Ω(θ)=λ|θ|=λ∑Dj=1|θj| Ω ( θ ) = λ | θ | = λ ∑ j = 1 D | θ j |

2.1.2.3 - 线性模型的非线性化

• 基函数： x2,log,exp x 2 , l o g , e x p ， 决策树
• 核化：带有正则的问题一般都是一个带有约束的优化问题，这样可以把原问题转换为对偶问题， 对偶问题中的向量的点积可以利用核函数来解决。 K(x,x′)=Φ(x)Φ(x′) K ( x , x ′ ) = Φ ( x ) Φ ( x ′ )
• 施加非线性的变换，深度学习中对输入的线性组合施加非线性的激活函数。

2.1.3 - 优化

梯度下降法：

w=w−λ∂∂wJ(w) w = w − λ ∂ ∂ w J ( w )

• 下降的步伐大小（学习率）非常重要：如果太小，收敛速度慢；如果太大，可能会出现overshoot the minimum的现象，如果学习率取值后发现函数值增长了，则需要减小学习率的值。
• 梯度下降求得的只是局部最小值，
  
  • 若二阶导数>0, 则目标函数为凸函数，局部极小值即为全局最小值。
  • 随机选择多个初始值，得到函数的多个局部极小值点。多个局部极小值点的最小值为函数的全局最小值。

更多的算法：SGD, Adam, RMSprop…

若采用梯度下降求解，需要损失函数对参数?的一阶导数，二阶导数用来判断函数是否为凸函数， XGBoost优化求解时，需要损失函数对预测函数 f f 的一阶导数和二阶导数

2.2 - 分类回归树

• 模型：树
• 参数：分裂的特征及阈值
• 目标函数
  
  • 损失函数：L2损失/Gini指数
  • 正则项：树的节点数目，叶子节点分数的平方和、
• 优化
  
  • 建树
  • 剪枝

Classification And Regression Tree(CART): 是一个用于监督学习的非参数模型，是一棵二叉树。

2.2.1 - 模型及参数

模型：

f(x)=∑m=1Mwm1(x∈Rm) f ( x ) = ∑ m = 1 M w m 1 ( x ∈ R m )

参数：分裂的特征及阈值

树模型很容易过拟合所以很多策略都是在防止模型过拟合，如，提前终止、剪枝、Bagging…

J(T)=C(T)+λΩ(T) J ( T ) = C ( T ) + λ Ω ( T )

其中， C(T) C ( T ) 表示模型对训练数据的预测误差，即模型和训练数据的拟合程度； Ω(T) Ω ( T ) 表示模型复杂度。

实现优化目标函数 J(T) J ( T ) 的过程分为建树和剪枝：建树仅仅考虑了提高信息增益（或者信息增益率，或者纯度等），对训练数据进行更好的拟合，从而实现了损失最小化；而剪枝则降低了模型的复杂度，使得模型具有更好的泛化能力。所以树的生成是学习局部的模型， 树的剪枝是学习全局的模型。

梯度下降法系列是一种优化的形式，在决策树中通过建树和剪枝操作来进行目标函数的最优化。

2.2.2 - 建树

样本集合为 D D , 选择特征 j j , 和分裂阈值 tm t m ，组成候选分裂 θ=(j,tm) θ = ( j , t m ) ，将样本分为两个分支 DL D L , DR D R

• DL(j,tm)={(xi,yi)|xij≤tm} D L ( j , t m ) = { ( x i , y i ) | x i j ≤ t m }
• DR(j,tm)={(xi,yi)|xij>tm} D R ( j , t m ) = { ( x i , y i ) | x i j > t m }

分裂原则：各分支的样本越纯净越好
- 不纯净性度量函数：

G(D,j,tm)=NLNH(DL)+NRNH(DR) G ( D , j , t m ) = N L N H ( D L ) + N R N H ( D R )

其中 H(D) H ( D ) 衡量样本的不确定性或者不纯净度。

(j∗,t∗m)=argminj,tmG(D,j,tm) ( j ∗ , t m ∗ ) = a r g m i n j , t m G ( D , j , t m )

回归问题

H(D)=∑i∈D(yi−y¯)2 H ( D ) = ∑ i ∈ D ( y i − y ¯ ) 2

分类问题

H(D)=Gini(D)=1−∑k=1K(|Dk||D|)2 H ( D ) = G i n i ( D ) = 1 − ∑ k = 1 K ( | D k | | D | ) 2

停止条件：

• 树的最大深度
• 分支样本足够纯净
• 分支数目足够少

优点

• 容易解释
• 不要求对特征做预处理
  
  • 能处理离散值和连续值混合的输入
  • 对特征的单调变换不敏感(只与数据的排序有关)
  • 能自动进行特征选择
  • 可处理缺失数据
• 可扩展到大数据规模

缺点

• 正确率不高，对数据比较敏感， 正好可以用作Boosting算法的弱学习器
• 模型不稳定，方差大， 可以使用Bagging算法得到随机森林来解决这个问题

2.2.3 - sklearn中的Tree

• 分类树：DecisionTreeClassifier

  class sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best',max_depth=None, min_samples_split=2, min_samples_leaf=1,min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_split=1e-07, class_weight=None,presort=False)

• 回归树：DecisionTreeRegressor

  class sklearn.tree.DecisionTreeRegressor(criterion='mse', splitter='best',max_depth=None, min_samples_split=2, min_samples_leaf=1,min_weight_fraction_leaf=0.0, max_features=None, random_state=None,max_leaf_nodes=None, min_impurity_split=1e-07, presort=False)

2.3 - 随机森林

分类回归树(CART)算法的缺点之一是高方差， 一种降低算法方差的方式是平均多个模型的预测：Bagging(Bootstrap aggregating)

2.3.1 - Bagging(bootstrap aggregation)

bootstrap：对N个样本的数据集 D D 进行有放回抽样，得到有N个样本的数据集 D′ D ′ 。

对N个样本的数据集 D D 进行bootstrap，在得到的数据集 Dt D t 上由弱学习器训练得到模型 ft f t 。重复 T T 次:

G(x)=∑t=1Tft(x) G ( x ) = ∑ t = 1 T f t ( x )

2.3.2 - random forest

将bagging框架中的弱学习器定为决策树CART，得到随机森林算法。 但是由于只是训练数据有一些不同，对回归树算法进行Bagging得到的多棵树高度相关，因此带来的方差减少有限。所以随机森林在每一个弱学习器的学习过程中，随机的选择一部分特征进行树的构建，或者随机组合一些特征作为新的分裂特征，以此来增加随机性，降低各个子树之间的相关性。

随机森林算法可以概括为以bagging为框架，弱学习器为decision tree， 并且添加了更多的随机因素的集成算法。

可并行