梯度下降、多元线性回归
介绍
最近在学习机器学习,看的是周志华的西瓜书和吴恩达的斯坦福公开课 CS229 。虽然这两个教程都是经典,但个人感觉斯坦福 CS229 对小白更友好一些。
这篇文章介绍一下线性回归,并利用梯度下降对多元线性回归方程进行推导。
线性回归
线性回归是机器学习中的一个非常基础的概念,也是非常重要的概念。百度百科的解释是:
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达形式为y = w’x+e,e为误差服从均值为0的正态分布。
通俗地讲,就是我们输入一组训练数据,然后根据这组数据计算出一个线性模型,根据这个线性模型我们就可以对所有的输入进行输出的预测。下面来看一下线性回归。
首先,根据机器学习的概念,先来定义以下几个变量的意义:
- m:样本的数量
- x:输入变量,向量
- n:输入变量的维数,即特征值的数目
- y:输出变量,数值
- ( x , y x,y x,y):一个训练实例
- ( x ( i ) , y ( i ) x^{(i)} , y^{(i)} x(i),y(i)):第 i 个训练实例
如果我们有 m 个样本,第 i 个训练实例表示为( x ( i ) , y ( i ) x^{(i)} , y^{(i)} x(i),y(i))。那么线性回归模型可以表示为:
(1.1) h ( θ ) = θ 0 + θ 1 x + θ 2 x 2 + ⋯ + θ n x n h(\theta) = \theta_0 + \theta_1x +\theta_2x^2 + \cdots + \theta_nx^n \tag{1.1} h(θ)=θ0+θ1x+θ2x2+⋯+θnxn(1.1)
写成矩阵的形式就是:
(1.2) h θ ( x ) = ∑ 0 n θ i x i = θ T x h_\theta(x) = \sum_0^n\theta_ix^i = \theta^Tx \tag{1.2} hθ(x)=0∑nθixi=θTx(1.2)
其中, h θ ( x ) h_\theta(x) hθ(x)表示以 θ \theta θ 为参数, θ \theta θ 和 x 都是 n+1 维向量,其中 x 0 x_0 x0 = 1。
式(1.2)就是多元线性回归方程,然而我们的重点不是列出这个式子,而是求解参数 θ \theta θ 来使得这个模型能够很好地对输出进行预测。由最小二乘法可知,要使该模型预测尽可能准确,应该让所有的实例到式(1.1)的距离最小,也就是欧几里得距离最小。
这样,我们就可以使用函数的均方差来进行计算,函数均方差可以由下面式子表示:
(1.3) J θ ( x ) = 1 2 ∑ 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J_\theta(x) = \frac12\sum_1^m(h_\theta(x^{(i)}) - y^{(i)})^2 \tag{1.3} Jθ(x)=211∑m(hθ(x(i))−y(i))2(1.3)
注意,这里的 1 2 \frac12 21 是仿照 CS229 课程的方式,为了以后的计算方便而设定的。函数均方差越小,模型对数据的拟合就越高。所以我们的目标就是找到使得均方差最小的参数 θ \theta θ。为了求该参数,就引入了梯度下降的方法。
梯度下降
梯度下降是一种计算局部最小值的一种方法,通俗地讲,梯度下降的思想就是每次走一小步,每一步都是往当前能够下降最大的方向前进。这样,最后就可以达到一个局部最小值。下面具体来讲解一下。
对于方程而言,每次下降的多少取决于步长 α \alpha α 和单位长度下降的多少,即偏导数。相同的步长,偏导数越大,则下降越快。先求线性回归的偏导:
(2.1) ∂ θ j J θ ( x ) = ∂ θ j 1 2 ( h θ ( x ) − y ) 2 = ( h θ ( x ) − y ) ∂ θ j ( h θ ( x ) − y ) = ( h θ ( x ) − y ) ∂ θ j ( ∑ 0 m x i θ i − y ) = ( h θ ( x ) − y ) x j \frac{\partial}{\theta_j}J_\theta(x) = \frac{\partial}{\theta_j} \frac12(h_\theta(x) - y)^2 \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (h_\theta(x) - y)\frac{\partial}{\theta_j}(h_\theta(x) - y) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = (h_\theta(x) - y)\frac{\partial}{\theta_j}(\sum_0^mx_i\theta_i - y) \\ \ \ \ \ \ \ \ \ \ =(h_\theta(x) - y)x_j \tag{2.1} θj∂Jθ(x)=θj∂21(hθ(x)−y)2 =(hθ(x)−y)θj∂(hθ(x)−y) =(hθ(x)−y)θj∂(0∑mxiθi−y) =(hθ(x)−y)xj(2.1)
对于只有一个训练样本的训练组而言,每走一步, θ j \theta_j θj的表示方式就可以写成:
(2.2) θ j = θ j + α ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) \theta_j = \theta_j + \alpha(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)} \tag{2.2} θj=θj+α(y(i)−hθ(x(i)))xj(i)(2.2)
因此,当有 m 个训练实例的时候,该公式就可以写为:
(2.3) θ j = θ j + α ∑ i = 0 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) \theta_j = \theta_j + \alpha\sum_{i = 0}^m(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)} \tag{2.3} θj=θj+αi=0∑m(y(i)−hθ(x(i)))xj(i)(2.3)
这样,每次根据所有数据求出偏导数,然后根据特定的步长 α \alpha α,就可以不断更新 θ j \theta_j θj,直到其收敛。通常,当其无限趋近于 0 或不能继续下降的时候,就可以说它已经收敛,即到达局部最小值。
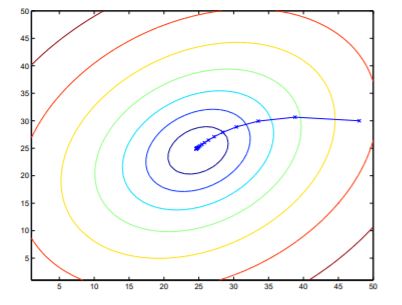
具体描述可以看下图:
距离最小值越近,偏导数越小, θ j \theta_j θj的变化就越小。该图直接到达了全局最小值,这种情况当然是最好的,但通常利用梯度下降求得的只是局部最小值。
梯度下降的算法有一个最大的问题:每次更新,都要利用所有的数据,当数据量十分大的时候,这会使效率变得特别低。因此,又出现了增强梯度下降,每次只用训练集中的一个数据,即:
for i to m :
θ j = θ j + α ( y ( i ) − h θ ( x i ) ) x j ( i ) \ \ \ \ \ \ \ \ \ \ \ \ \ \theta_j = \theta_j + \alpha(y^{(i)} - h_\theta(x^{i}))x_j^{(i)} θj=θj+α(y(i)−hθ(xi))xj(i)
这样的话,整个训练集只需遍历一遍就可以到达局部最小值。
正规方程组
在推导之前,首先定义一些符号:
梯度符号 ∇ A \nabla_A ∇A:
∇ A f ( A ) = [ ∂ f A 11 ⋯ ∂ f A 1 n ⋮ ⋱ ⋮ ∂ f A m 1 ⋯ ∂ f A m n ] \nabla_Af(A) = \begin{bmatrix} \frac{\partial f}{A_{11}} & \cdots & \frac{\partial f}{A_{1n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial f}{A_{m1}} & \cdots & \frac{\partial f}{A_{mn}} \\ \end{bmatrix} ∇Af(A)=⎣⎢⎡A11∂f⋮Am1∂f⋯⋱⋯A1n∂f⋮Amn∂f⎦⎥⎤
矩阵的迹 t r A trA trA:
t r A = ∑ i = 1 n A i i trA = \sum_{i=1}^n A_{ii} trA=i=1∑nAii
需要记住的几点性质:
(3.1) t r A B C = t r C A B = t r B C A trABC = trCAB = trBCA \tag{3.1} trABC=trCAB=trBCA(3.1)
(3.2) t r A = t r A T trA = trA^T \tag{3.2} trA=trAT(3.2)
(3.3) t r ( A + B ) = t r A + t r B tr(A + B) = trA + trB \tag{3.3} tr(A+B)=trA+trB(3.3)
(3.4) t r a A = a t r A traA = atrA \tag{3.4} traA=atrA(3.4)
二者结合的性质:
(3.5) ∇ A t r A B = B T \nabla_AtrAB = B^T \tag{3.5} ∇AtrAB=BT(3.5)
(3.6) ∇ A T f ( A ) = ( ∇ A f ( A ) ) T \nabla_{A^T}f(A) = (\nabla_Af(A))^T \tag{3.6} ∇ATf(A)=(∇Af(A))T(3.6)
(3.7) ∇ A t r A B A T C = C A B + C T A B T \nabla_AtrABA^TC = CAB + C^TAB^T \tag{3.7} ∇AtrABATC=CAB+CTABT(3.7)
(3.8) ∇ A ∣ A ∣ = ∣ A ∣ ( A − 1 ) T \nabla_A|A| = |A|(A^{-1})^T \tag{3.8} ∇A∣A∣=∣A∣(A−1)T(3.8)
推导
X和Y的矩阵表示为:
X = [ x ( 1 ) T ⋮ x ( m ) T ] X = \begin{bmatrix} {x^{(1)}}^T\\ \vdots\\ {x^{(m)}}^T\\ \end{bmatrix} X=⎣⎢⎢⎡x(1)T⋮x(m)T⎦⎥⎥⎤
Y = [ y ( 1 ) ⋮ y ( m ) ] Y = \begin{bmatrix} y^{(1)} \\ \vdots \\y^{(m)}\end{bmatrix} Y=⎣⎢⎡y(1)⋮y(m)⎦⎥⎤
计算 X θ − Y X\theta - Y Xθ−Y得:
X θ − Y = [ x ( 1 ) T θ ⋮ x ( m ) T θ ] − [ y ( 1 ) ⋮ y ( m ) ] = [ h θ ( x ( 1 ) ) − y ( 1 ) ⋮ h θ ( x ( m ) ) − y ( m ) ] X\theta - Y = \begin{bmatrix} {x^{(1)}}^T\theta\\ \vdots\\ {x^{(m)}}^T\theta\\ \end{bmatrix} - \begin{bmatrix} y^{(1)} \\ \vdots \\y^{(m)}\end{bmatrix} = \begin{bmatrix} h_\theta(x^{(1)}) - y^{(1)}\\ \vdots\\ h_\theta(x^{(m)}) - y^{(m)}\\ \end{bmatrix} Xθ−Y=⎣⎢⎢⎡x(1)Tθ⋮x(m)Tθ⎦⎥⎥⎤−⎣⎢⎡y(1)⋮y(m)⎦⎥⎤=⎣⎢⎡hθ(x(1))−y(1)⋮hθ(x(m))−y(m)⎦⎥⎤
由矩阵运算 ∑ i z i 2 = z T z \sum_i{z_i}^2 = z^Tz ∑izi2=zTz可以得到:
J θ ( x ) = 1 2 ∑ 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 ( X θ − Y ) T ( X θ − Y ) J_\theta(x) = \frac12\sum_1^m(h_\theta(x^{(i)}) - y^{(i)})^2 = \frac12(X\theta - Y)^T(X\theta - Y) Jθ(x)=211∑m(hθ(x(i))−y(i))2=21(Xθ−Y)T(Xθ−Y)
推导过程如下:
由偏导等于0得:
X T X θ = X T Y ⟹ θ = ( X T X ) − 1 X T Y X^TX\theta = X^TY \Longrightarrow \theta = (X^TX)^{-1}X^TY XTXθ=XTY⟹θ=(XTX)−1XTY
这样,我们就求出了参数。
即多元线性回归模型为:
f ( X i ) = x i T ( X T X ) − 1 X T Y f (Xi) = {x_i}^T(X^TX)^{-1}X^TY f(Xi)=xiT(XTX)−1XTY
总结
推导的重点在后面,可以多看几遍。如果实在记不住过程,直接背下来即可,这部分相对而言较简单,学完后面再回来看,或许就觉得理所当然了。
参考文献
感谢 CS229 课程和其他博主的博客。
- 线性规划、梯度下降、正规方程组——斯坦福ML公开课笔记1-2
- 斯坦福大学公开课CS229课件